構(gòu)造函數(shù)在導(dǎo)數(shù)中的應(yīng)用

■甘肅省白銀市第一中學(xué) 胡貴平

構(gòu)造函數(shù)是解導(dǎo)數(shù)問題的基本方法，怎樣根據(jù)初等函數(shù)的導(dǎo)數(shù)公式和導(dǎo)數(shù)的基本運算法則，合理地構(gòu)造出輔助函數(shù)，借助函數(shù)的性質(zhì)，解決抽象函數(shù)的導(dǎo)數(shù)問題呢?下面舉例說明。

類型一：f(x)+xf'(x)構(gòu)造函數(shù)F(x)=xf(x)

例1(2018年甘肅蘭州一診)已知函數(shù)y=f(x)是定義域R上的偶函數(shù)，且當(dāng)x＞0時，不等式f(x)+x·f'(x)＜0成立，若a=30.2f(30.2)，b=(logπ2)f(logπ2)，c=，則a，c，b之間的大小關(guān)系為( )。

A.a＞c＞b B.c＞a＞b

C.c＞b＞a D.b＞a＞c

解：記函數(shù)g(x)=xf(x)，則g'(x)=f(x)+xf'(x)，因為當(dāng)x＞0時，不等式f(x)+x·f'(x)＜0成立，所以x＞0，g'(x)＜0，所以g(x)在(0，+∞)上單調(diào)遞減，又因為函數(shù)y=f(x)是定義域R上的偶函數(shù)，所以函數(shù)g(x)=xf(x)為奇函數(shù)，且在R上單調(diào)遞減，因為1＜30.2＜2，0＜logπ2＜1，log2=-2，所以-2＜logπ2＜30.2，所以c＞b＞a，故選C。

變式：nf(x)+xf'(x)構(gòu)造函數(shù)F(x)=xnf(x)。

F(x)=xnf(x)，則F'(x)=nxn-1f(x)+xnf'(x)=xn-1[nf(x)+xf'(x)]。

例2(2009年天津文12)設(shè)函數(shù)f(x)在R上的導(dǎo)函數(shù)為f'(x)，且2f(x)+xf'(x)＞x2，下面的不等式在R內(nèi)恒成立的是( )。

A.f(x)＞0 B.f(x)＜0

C.f(x)＞x D.f(x)＜x

解：由已知，首先令x=0得f(x)＞0，排除B，D。

令g(x)=x2f(x)，則g'(x)=x[2f(x)+xf'(x)]。

綜上，f(x)＞0。故選A。

類型二：xf'(x)-f(x)構(gòu)造函數(shù)F(x)

例3(2015年全國新課標(biāo)Ⅱ卷理12)設(shè)函數(shù)f'(x)是奇函數(shù)f(x)(x∈R)的導(dǎo)函數(shù)，f(-1)=0，當(dāng)x＞0時，xf'(x)-f(x)＜0，則使得f(x)＞0成立的x的取值范圍是( )。

A.(-∞，-1)∪(0，1)

B.(-1，0)∪(1，+∞)

C.(-∞，-1)∪(-1，0)

D.(0，1)∪(1，+∞)

解：記函數(shù)g(x)=，則g'(x)=因為當(dāng)x＞0時，xf'(x)-f(x)＜0，故當(dāng)x＞0時，g'(x)＜0，所以g(x)在(0，+∞)上單調(diào)遞減。又因為函數(shù)f(x)(x∈R)是奇函數(shù)，故函數(shù)g(x)是偶函數(shù)，所以g(x)在(-∞，0)上單調(diào)遞減，且g(-1)=g(1)=0。當(dāng)0＜x＜1時，g(x)＞0，則f(x)＞0;當(dāng)x＜-1時，g(x)＜0，則f(x)＞0。綜上所述，使得f(x)＞0成立的x的取值范圍是(-∞，-1)∪(0，1)，故選A。

變式：xf'(x)-nf(x)構(gòu)造函數(shù)F(x)

例4(2017年安徽省蚌埠二中等四校聯(lián)考)定義在區(qū)間(0，+∞)上的函數(shù)f(x)滿足:2f(x)＜xf'(x)＜3f(x)對x∈(0，+∞)恒成立，其中f'(x)為f(x)的導(dǎo)函數(shù)，則( )。

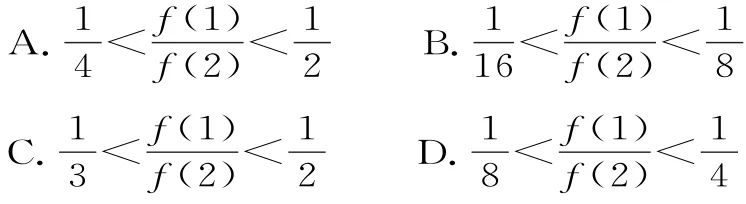
類型三：f'(x)+f(x)構(gòu)造函數(shù)F(x)=f(x)ex

例5設(shè)f(x)是R上的可導(dǎo)函數(shù)，且f'(x)≥-f(x)，f(0)=1，f(2)=。則f(1)的值為____。

解：由f'(x)≥-f(x)得f'(x)+f(x)≥0，所 以 exf'(x)+exf(x)≥0，即[exf(x)]'≥0。設(shè)函數(shù)F(x)=exf(x)，則此時有1=F(2)≥F(0)=1，故F(x)=exf(x)=1，f(1)=。

變式：f'(x)+nf(x)構(gòu)造函數(shù)F(x)=enxf(x)。

F(x)=enxf(x)，F(xiàn)'(x)=f'(x)enx+nenxf(x)=enx[f'(x)+nf(x)]。

例6已知函數(shù)f(x)滿足:f(x)+2f'(x)＞0，那么下列不等式成立的是( )。

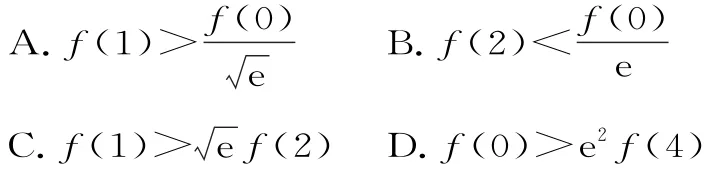
解：設(shè)F(x)=f(x)。

因為f(x)+2f'(x)＞0，所以F'(x)＞0，則F(x)在定義域上單調(diào)遞增，所以F(1)＞F(0)，則，故答案為A。

類型四：f'(x)-f(x)構(gòu)造函數(shù)F(x)=

例7(2017年南昌市三模)已知函數(shù)f'(x)是函數(shù)f(x)的導(dǎo)函數(shù)，f(1)=，對任意實數(shù)x，都有f(x)-f'(x)＞0，則不等式f(x)＜ex-2的解集為( )。……