2018年高考全國課標Ⅰ卷理科第21題的多角度證明

■福建省泉州市第七中學 彭耿鈴

2018年全國課標Ⅰ卷的理科第21題為導數解答題，形式上有“簡約而不簡單”之感，試題以常規的知識和方法為載體，挖掘了數學的學科本質，較好地考查了考生的綜合能力和學科素養，有利于科學選拔創新人才。本文旨在探究此題型規律，揭示解題方法，提供解題規律，希望對讀者以后參加高考大有幫助。

原題(2018年課標Ⅰ卷理科數學第21題)已知函數f(x)=-x+alnx。

(1)討論f(x)的單調性;(2)若f(x)存在兩個極值點x1，x2，證明:＜a-2。

解：(1)略。(2)由(1)知，當且僅當a＞2時f(x)存在兩個極值點。由于f(x)的兩個極值點x1，x2滿足x2-ax+1=0，所以x1+x2=a，x1x2=1，不妨設x1＜x2，則x2＞1。由于＜a-2等＜a-2，即證明:ln x2-lnx1＜x2-x1。

法二(利用對數均值不等式):要證明lnx2-lnx1＜x2-x1，即證明＞1，由對數均值不等式(當b＞a＞0時，b＞=1，證畢。

法三(轉化法):因為x1+x2=a，x1x2=1，不妨設x1＜x2，則0＜x1＜1，故證明＜a-2等價于證明x1+x2-2，即證明f(x1)-+2x1＞f(x2)-+2x2，令h(x)=f(x)-x2+2x，則證明原不等式轉化為證明h(x1)＞h(x2)，即證明x＜1)，令F(x)=h(x)-h）(0＜x＜11111)，則:

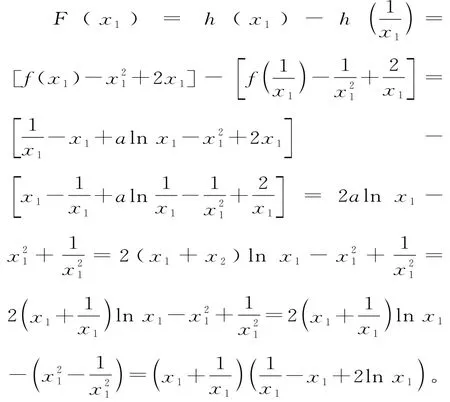
法四(變換主元):由(1)知，f(x)存在兩個極值點當且僅當a＞2，且f(x)的兩個極值點x1，x2滿足x2-ax+1=0，所以x1x2=1，不妨設x1＜x2，則，故x2-x1=，因為等價于證明＜a-2，即證明ln＜x-x，即證明

21(a＞2)，即證明＜0(a＞2)，構造函數h(a)=(a＞2)，則h'(a)=2·＜0對a＞2恒成立，故h(a)=在(2，+∞)上單調遞減，故h(a)＜h(2)=0，即對a＞2恒成立，證畢。

法五(定義法):由(1)知，f(x)存在兩個極值點當且僅當a＞2。由于f(x)的兩個極值點x1，x2滿足x2-ax+1=0，所以x1+x2=a，x1x2=1，不妨設x1＜x2，則x2＞1。由于-1+a·=-2+，由斜率及導數的幾何意義可知:故要證＜a-2，只需要證[f'(x)]max≤a-2，即只需要證a2≥a+2(a＞2)，顯然成立，證畢。

法六(構造法):由(1)知，f(x)存在兩個極值點當且僅當a＞2。由于f(x)的兩個極值點x1，x2滿足x2-ax+1=0，所以x1+x2=a，x1x2=1，不 妨 設 x1＞x2，則＜a-2?f(x1)-f(x2)＜(a-2)(x1-x2)，即等價于證明f(x1)-(a-2)·x1＜f(x2)-(a-2)x2(*)。構造函數g(x)=f(x)-(a-2)x=-x+alnx-(a-2)x，則(*)等價于證明:g(x1)＜g(x2)。因為g'(x)=由f'(x)=0得x2-ax+1=0，即x2=ax-1，故g'(x)==2-a，因為a＞2，所以g'(x)＜0，故g(x)在(0，+∞)上單調遞減，由x1＞x2知，g(x1)＜g(x2)，證畢。

以上的幾種證明方法更容易接近問題的本質，使得同學們更容易接受，解題思維更加流暢，更容易地尋找解題的方向。……