淺析構造可導抽象函數求解策略

■重慶市鐵路中學校 何成寶

抽象函數因為沒有具體的解析式，理解研究起來比較困難，所以是高中數學函數部分的難點。但抽象函數問題既能考查函數的概念和性質，又能考查同學們的思維能力，因此備受命題者的青睞。求解此類試題關鍵是抓住原函數和導函數的關系式特征，構造出對應的可導抽象函數。下面舉例說明，以供同學們參考。

一、構造f(x)±g(x)型函數

形如f'(x)±g'(x)的結構，則可構造函數h(x)=f(x)±g(x)，例如:

(1)f'(x)-g'(x)＞0，構造函數h(x)=f(x)-g(x);

(2)f'(x)+g'(x)＞0，構造函數h(x)=f(x)+g(x)。

例1若定義在R上的函數f(x)滿足f(0)=-1，其導函數f'(x)滿足f'(x)＞k＞1，則下列結論中一定錯誤的是( )。

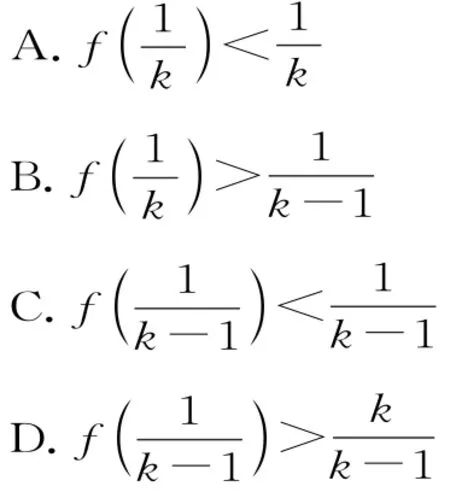
解析：構造函數g(x)=f(x)-kx，則g'(x)=f'(x)-k＞0，所以g(x)在R上單調遞增。令g(0)，也即＞-1，化簡得，故選C。

練習1：定義在R上的函數f(x)滿足:f(-x)+f(x)=x2，當x＜0時，f'(x)＜x，則不等式f(x)+≥f(1-x)+x的解集為____。

解析：構造函數g(x)=f(x)-，當x＜0時，g'(x)=f'(x)-x＜0，說明g(x)在(-∞，0)上為減函數。而g(x)+g(-x)=f(x)+f(-x)-x2=0，所以g(x)為奇函數。又f(0)=0，g(0)=0，所以g(x)在R上為減函數。

二、構造f(x)·g(x)型函數

形如f'(x)·g(x)+f(x)·g'(x)的結構，可構造函數h(x)=f(x)·g(x)。

(1)若xf'(x)+f(x)＞0，則[xf(x)]'=xf'(x)+f(x)＞0，故可構造函數h(x)=x·f(x);

(2)若 xf'(x)+nf(x)＞0，則[xn·f(x)]'=xn-1[xf'(x)+nf(x)]＞0，可構造函數h(x)=xn·f(x);

(3)若 f'(x)+f(x)＞0，則[ex·f(x)]'=ex[f'(x)+f(x)]＞0，故可構造函數h(x)=exf(x);

(4)若 f'(x)+nf(x)＞0，則[enx·f(x)]'=enx[f'(x)+nf(x)]＞0，故可構造函數h(x)=enx·f(x)。

例2設函數f(x)是定義在(-∞，0)上的可導函數，其導函數為f'(x)，且有2f(x)+xf'(x)＞x2，則不等式 (x+2019)2f(x+2019)-4f(-2)＞0的解集為____。

解析：構造函數g(x)=x2f(x)(x＜0)，當x＜0時，g'(x)=2xf(x)+x2f'(x)=x[2f(x)+xf'(x)]＜x3＜0，則g(x)在(-∞，0)上是減函數。因為(x+2019)2f(x+2019)＞(-2)2f(-2)，所以g(x+2019)＞g(-2)，x+2019＜-2，即x＜-2021，所以不等式的解集為(-∞，-2021)。

練習2：已知函數f(x)滿足x2f'(x)+，則當x＞0時，f(x)( )。

A.有極大值，無極小值

B.有極小值，無極大值

C.既有極大值又有極小值

D.既無極大值也無極小值

解析：構造函數g(x)=x2f(x)，g'(x)=2xf(x)+x2f'(x)=，所 以f'(x)=。令h(x)=ex-2x2f(x)，h'(x)=ex-2[2xf(x)+x2f'(x)]=ex-。當0＜x＜2時，h'(x)＜0，h(x)單調遞減;x＞2時，h'(x)＞0，h(x)單調遞增，故h(x)min=h(2)=e2-8f(2)=0。因此，當x＞0時，h(x)≥0恒成立。因為，所以f'(x)≥0恒成立。因此，f(x)在(0，+∞)上單調遞增，f(x)無極大值，也無極小值，故選D。

練習3:設f(x)，g(x)分別是定義在R上的奇函數和偶函數，當x＜0時，f'(x)·g(x)+f(x)·g'(x)＞0，且g(-3)=0，則不等式f(x)·g(x)＜0的解集是( )。……