利用導數求解不等式恒成立問題的策略

■河南省洛陽市第一高級中學 宋甜甜

含參數不等式恒成立問題，是高中數學的難點之一，也是高考、數學競賽的熱點之一，怎樣處理這類問題呢?通過轉化可使恒成立問題得到簡化，下面就含參數不等式恒成立問題的解題策略舉例說明，僅供參考。

一、分離參數法

將原不等式分離參數，轉化為不含有參數的函數最值問題，利用導數求該函數的最值，根據要求得出參數的范圍。

例1已知函數f(x)=x3-x2+bx+1，若對任意的x∈[0，+∞)，都有f(x)≥0恒成立，求b的取值范圍。

解析：因為x3-x2+bx+1≥0，所以b≥x-x2-x1。 令g(x)=x-x2-， 則。當0＜x＜1時，g'(x)＞0;當x＞1時，g'(x)＜0。

故g(x)max=g(1)=-1，b≥-1。

點評：1.變量與參數的確定：本題中x的范圍已知，就將其視為變量，構造關于它的函數，將另一個字母b視為參數。

2.分離參數法遵循兩點原則：(1)已知不等式中兩個字母容易分離；(2)分參離數后，已知變量的函數解析式容易求出最值(或臨界值)。

3.一般地，若f(x)＞a恒成立，只需f(x)min＞a即可；若f(x)＜a恒成立，只需f(x)max＜a即可。

練習1：已知函數f(x)=x3+ax2-2ax+a2，若對任意的x∈(2，+∞)，都有f(x)＞a2恒成立，求a的取值范圍。

解析：因為x3+ax2-2ax+a2＞a2，且x＞2，所以。令g(x)=當2＜x＜4時，g'(x)＞0;當x＞4時，g'(x)＜0。

故g(x)max=g(4)=-8，b≥-8。

練習2:已知函數f(x)=x3+ax2+9x+a2，若對任意的x∈(0，+∞)，都有6xlnx+f'(x)≥0恒成立，求a的取值范圍。

解析：因為6xlnx+3x2+2ax+9≥0，且x＞0，所以2a≥-6lnx-3x-。

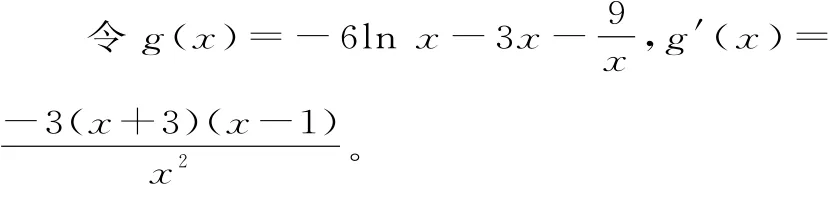
當0＜x＜1時，g'(x)＞0;

當x＞1時，g'(x)＜0。

故g(x)max=g(1)=-12，a≥-6。

二、函數最值法

將不等式問題轉化為含待求參數的函數最值問題，再利用導數求該函數的最值，然后構建不等式求解。

例2已知函數f(x)=x3+ax2+bx+a2，當a=0，b=-3時，證明:任意的x∈R，都有f(x)+2≥恒成立。

證明：當a=0，b=-3時，令g(x)=x3

min

故當x＞1時，g'(x)＞0;當x＜1時，g'(x)＜0。

g(x)min=g(1)=0，x3-3x+2-≥0恒成立。

點評：辨析“f(x)≥g(x)”型與“f(x1)≥g(x2)”型的差異：

1.對?x∈I，不等式f(x)≥g(x)恒成立，可轉化為求函數[f(x)-g(x)]min≥0。

2.對?x1，x2∈I，不等式f(x1)≥g(x2)恒成立，可轉化為求函數f(x)min≥g(x)max。

練習3：已知函數f(x)=x3+ax2+a2，若任意的x1，x2∈(0，+∞)且x1＜x2，都有f(x1)-f(x2)＜a(x1-x2)成立，求a的取值范圍。……