導數綜合題之謀略

■河南省平頂山市第一高級中學 劉海洋

■河南省平頂山市第一中學 張玲敏

眾所周知，導數的綜合應用題具有較高的難度，同學們“征服”它不僅要有勇氣，而且要有智慧。那么解答這類問題需要哪些謀略呢?下面舉例說明，供同學們參考。

一、利用分類討論思想探究函數性質問題

例1函數f(x)=x3+|x-a|(x∈R，a∈R)。

(1)若函數f(x)在R上為增函數，求a的取值范圍;

(2)若函數f(x)在R上不單調時，記f(x)在[-1，1]上的最大值、最小值分別為M(a)、m(a)，求M(a)-m(a)。

解析：由已知可得:

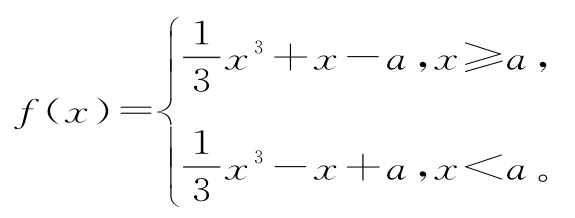
令h'(x)=0，得x=±1，所以h(x)在(-∞，-1)和(1，+∞)上是增函數，在(-1，1)上為減函數。

(1)分析可知，若要滿足f(x)在R上是增函數，則需要a≤-1。

故a的取值范圍為(-∞，-1]。

(2)因為函數f(x)在R上不單調，所以a＞-1。

當-1＜a＜1時，f(x)在(-∞，-1)上是增函數，在(-1，a)上是減函數，在[a，+∞)上是增函數。

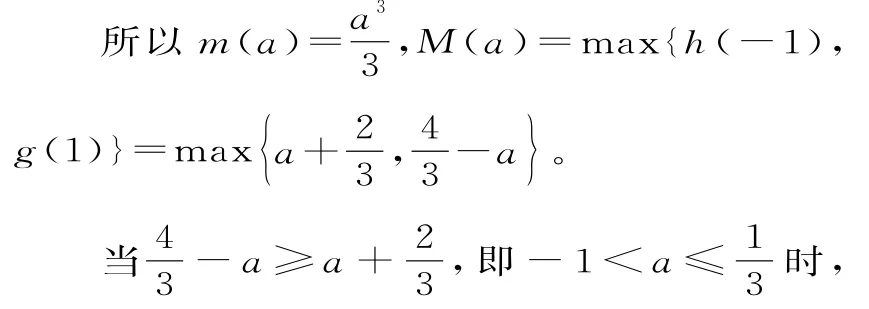
【方法感悟】

1.解答這類題的模板:

2.解答這類題的難點:

(1)何時討論參數?由于題目條件的不同，有的在求零點時討論，有的在列表時討論。

(2)如何討論參數?需要根據題目的條件而定，有時還需參考自變量的取值范圍，討論的關鍵是做到不重不漏。

二、利用數形結合思想探究函數的零點問題

例2設函數f(x)=lnx+，m∈R。

(1)當m=e(e為自然對數的底數)時，求f(x)的極小值;

解析：(1)由題設知，當m=e時，f(x)=

當x∈(0，e)時，f'(x)＜0，f(x)在(0，e)上單調遞減。

當x∈(e，+∞)時，f'(x)＞0，f(x)在(e，+∞)上單調遞增。

因此，f(x)的極小值為2。

則φ'(x)=-x2+1=-(x-1)(x+1)。

當x∈(0，1)時，φ'(x)＞0，φ(x)在(0，1)上單調遞增;

當x∈(1，+∞)時，φ'(x)＜0，φ(x)在(1，+∞)上單調遞減。

故x=1是φ(x)的唯一極值點，且是極大值點。

又φ(0)=0，結合y=φ(x)的圖像(如圖1)，可知:

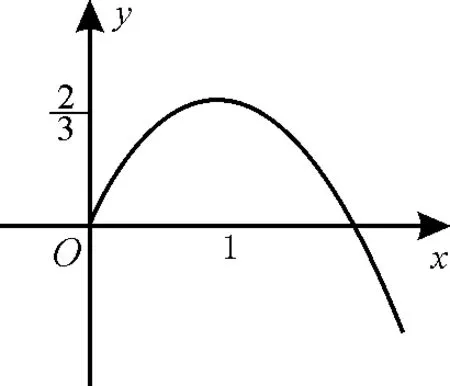
圖1

④當m≤0時，函數g(x)有且只有一個零點。

【方法感悟】

利用導數探究函數零點的一般思路:

(1)轉化為可用導數研究其函數的圖像與x軸(或直線y=k)在該區間上的交點問題;

(2)利用導數研究該函數在該區間上的單調性、極值(最值)、端點值等性質，進而畫出其圖像;