輪間距與雙輪共轉對飛機起落架擺振的影響分析

馮 飛， 羅 波， 張 策， 朱紅民

(中國運載火箭技術研究院，北京 100076)

前輪擺振，是飛機地面滑行過程中出現的常見現象[1]。盡管已被研究近一個世紀，現代飛機在研制和使用過程中仍無法完全避免擺振問題。自Broulhiet最早在汽車領域發現該問題后，前輪擺振在學術界普遍被認為是一種包含輪胎變形、支柱扭轉變形與側向變形等在內的多自由度耦合振動穩定性問題[2-3]。von Schlippe等[4-6]，提出了輪胎的點接觸模型與張線模型，奠定了擺振輪胎理論的基礎，指出了輪胎參數對擺振穩定性的影響。20世紀50年代起在美國Langley研究中心[7]開展的大量地面滑行試驗，為擺振的理論發展提供了基礎，起落架的結構參數的影響被學者廣泛研究。至20世紀80年代，起落架擺振的線性模型發展趨于完善，研究更多地關注了起落架與機體彈性、起落架與機身的聯接等因素的影響。此后，以平方阻尼、庫倫摩擦、結構間隙為代表的等非線性參數，成為前輪擺振研究的熱點[8-12]。Somieski指出，線性模型在精確預測起落架前輪系統的擺振行為時是無力的。21世紀起，隨著應用分岔理論(Applied Bifurcation Method)的逐漸完善，Thota等[13-15]提出了擺振分岔分析的基本步驟，采用分岔理論對非線性模型進行擺振分析成為前沿研究方向[16-17]。

本文提出了較為完善的擺振分岔分析方法，對包含輪胎變形、支柱扭轉、支柱側向彎曲等自由度在內的雙輪起落架非線性模型進行了研究，并分析了輪間距、雙輪共轉對擺振穩定性的影響。研究成果可用于指導飛機前起落架設計。

1 擺振動力學模型

1.1 坐標系與自由度

如圖1所示，一個垂向承載Fz的雙輪前起落架。安裝點離地高度Lg，起落架跟隨機身以恒定速度V，通過半徑為R、間距為D的兩個機輪在跑道上直線滑行。

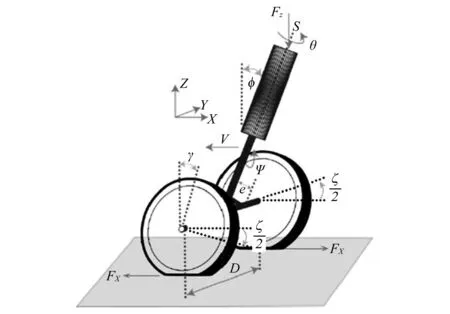
圖1 雙輪起落架擺振模型示意圖Fig.1 Schematic of a dual-wheel aircraft landing gear

滑行方向的反向定義為起落架坐標軸的X軸，水平向右為Y軸，垂向向上為Z軸。起落架支柱扭轉的平衡位置為中立，故不考慮機身的側向運動。在平穩滑行過程中，飛機沒有垂向位移，且起落架緩沖器的行程是不變的，故不考慮起落架的垂向位移。

(1)起落架支柱可繞定向軸S轉動，轉角為θ。

(2)繞X軸方向，起落架支柱存在側向彎曲變形ψ。

(3)左右兩個輪胎的側向位移λ1和λ2用于描述輪胎的變形。

(4)輪軸扭轉變形的自由度ξ，用于共轉雙輪之間的相互作用。如將輪軸扭轉變形ξ至零，則表征雙輪不共轉。

1.2 動力學方程

雙輪共轉的擺振動力學方程，可表述為式(1)～式(5)。

(1)

(2)

(3)

(4)

(5)

式(1)和式(2)分別為起落架支柱扭轉與側向彎曲自由度的平衡方程；式(3)和式(4)為基于von Schlippe的張線理論的輪胎變形協調方程；式(5)為輪軸扭轉變形自由度的平衡方程。

在后文方程的描述中，為便于書寫，略去表征左右輪胎的下角標i。

1.2.1起落架支柱扭轉方程

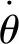
Mkθ=kθ·θ

(6)

(7)

式中：MF為輪胎作用于支柱扭轉自由度的組合力矩，包含輪胎非線性扭轉回正力矩Mkδ和輪胎非線性側向回復力Fkλ產生的力矩，如式(8)

MF=Mkδ+Fkλ·eeff

(8)

輪胎非線性扭轉回正力矩Mkδ用式(9)進行描述。在輪胎的側滑極限δm范圍內，回正力矩Mkδ隨側偏角δ按正弦規律變化；在側滑極限δm范圍外，輪胎發生了側滑，回正力矩Mkδ等于零。

(9)

輪胎非線性側向回復力Fkλ根據實驗數據進行擬合，可表達為輪胎側向剛度系數kλ、側偏角δ和垂向載荷FZ的函數，如式(10)所示

Fkλ=kλarctan(7.0 tanδ)cos(0.95arctan(7.0 tanδ))FZ(10)

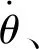
(11)

(12)

定向軸S與Z軸之間的前傾角φ，使得機輪的轉向角ζ并不嚴格等于起落架支柱的扭轉角θ，而是滿足式(13)所述的關系

ζ=θcos(φ)

(13)

定向軸S距離機輪的輪心存在機械穩定距e。前傾角φ的存在產生了幾何穩定距eeff，使得等效穩定距滿足式(14)

eeff=ecosφ+(R+esinφ)tanφ

(14)

(15)

在起落架滑行過程中，左右機輪承受的垂向載荷FZ1和FZ2并不相等。根據力矩平衡關系[19]，可按式(16)進行計算

(16)

式中：kv為輪胎的垂向壓縮剛度；γ為支柱前傾角導致的輪盤平面側傾角，可表達為式(17)

γ=θsin(φ)

(17)

1.2.2起落架支柱側向彎曲變形方程

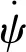
Mkψ=kψ·ψ

(18)

(19)

式中：Mλψ為輪胎非線性側向回復力產生的力矩，如式(20)所示

Mλψ=FkλLgcos(ζ)cos(φ)

(20)

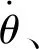
(21)

1.2.3輪胎變形協調方程

起落架支柱的扭轉與側向彎曲變形，通過輪胎的側向力進行耦合作用。機輪的輪胎模型基于張線理論建立，以輪胎觸地點中心線的側向位移λ和側偏角δ作為輪胎變形量。其中，輪胎的側偏角δ被定義為輪胎觸地點中心線的側向位移λ和輪胎松弛長度σ的函數，可表達為式(22)

δ=arctan(λ/σ)

(22)

輪胎相關的其余力和力矩見1.2.1節，不再贅述。

1.2.4輪軸扭轉變形自由度的平衡方程

式(5)描述了考慮雙輪共轉條件下的輪軸扭轉變形。如將變量ξ至零，則表征雙輪不共轉。

1.3 參數取值與延拓范圍

文中參數的含義與取值參見表1[20]。參數取值基于A320的前起落架數據。考慮到參數分岔圖像的完整性，部分參數的選取，如前向滑行速度等，可能超過實際的取值范圍。

表1 參數取值表Tab.1 Value of parateters

2 擺振分岔分析方法

擺振動力學方程組，可以改寫為式(23)的形式

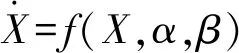
(23)

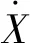
擺振分岔分析步驟如下：

步驟1確定平衡點。

在不考慮轉彎的前向滑行擺振分析中，希望出現的系統平衡狀態為各狀態變量中立的零平衡狀態，即起落架支柱無扭轉角與側向彎曲變形，輪胎觸地點中心線無側向位移等。故在擺振分岔分析中，僅分析零平衡狀態下的穩定性及相應Hopf分岔(及周期振蕩解)的分岔特性。

步驟2尋找Hopf分岔點。

在確定平衡狀態后，固定包含第二個控制參數β在內的其余所有參數不變，連續地變換第一個控制參數α的取值，計算控制參數α不同取值情況下，系統零平衡狀態的所有特征值。

若Jacobi矩陣的所有特征值λ1，λ2，…,λn滿足Reλ<0，零平衡狀態則是穩定的。隨著控制參數α的連續變化，所有特征值λ1,λ2,…,λn也連續變化。若發現控制參數在某個取值α=αH時，某一對特征值出現了Reλi,j=0情況，則系統出現了Hopf分岔。并稱控制參數α=αH為系統零平衡狀態的Hopf分岔點，簡稱為Hopf分岔點。

步驟3Hopf分岔點的單參數延拓。

選取任一Hopf分岔點，仍僅連續變換第一個控制參數α的取值，采用延拓算法，對各特征量隨控制參數的變化進行計算。

圖2為采用前向滑行速度為控制變量進行單參數延拓的計算結果。

步驟4Hopf分岔點的雙參數延拓。

在獲得第一個控制參數α的Hopf分岔點α=αH的基礎上，增加第二個控制參數β，求解二維控制參數(α,β)平面內的Hopf分支線。

圖2 Hopf分岔特征量隨滑行速度的變化曲線Fig.2 Curves of characteristic parameter varying with forward speed

圖3為采用前向滑行速度和垂向載荷為控制變量進行雙參數延拓的計算結果。觀察可得：兩條Hopf分岔曲線交于2點，稱為雙Hopf分岔點，圖中表示為“HH”；其中，一條封閉的Hopf分岔點上出現了2個Bautin分岔點，圖中表示為“B”。Bautin分岔點意味著在當前點Hopf分岔曲線發生了分岔。分岔出的一分支(圖2中兩個Bautin分支點之間上方的曲線)為不穩定的極限環的邊界，擺振分岔分析并不關心；另一支為穩定的極限環的邊界，表征擺振穩定區和不穩定區的邊界，有待進一步求解[21]。

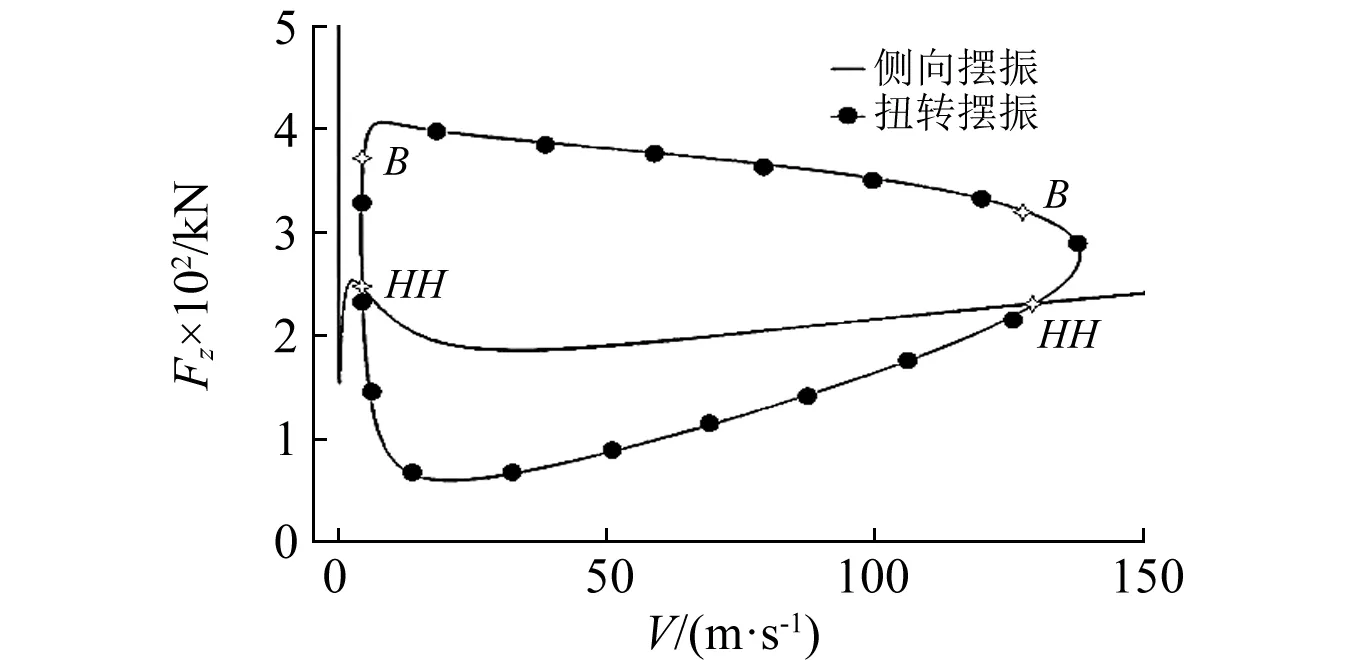
圖3 以垂向載荷、滑行速度為控制變量的分岔圖(1)Fig.3 Bifurcation map in vertical load-forward speed plane(1)

步驟5Bautin分岔點的雙參數延拓。

以Bautin分岔點為起點，延拓計算Hopf分支線分岔后的穩定分支。

如圖4所示，新計算獲得的分支線即擺振穩定區的邊界。由此，擺振分岔計算的二維相圖完成；獲得了擺振穩定與非穩定區域圖，詳見圖5。如圖5所示，起落架擺振在相圖上可直觀地進行分辨，包括以支柱扭轉為主體的扭轉擺振和以支柱側向彎曲變形為主體的側向彎曲擺振(簡稱側向擺振)。

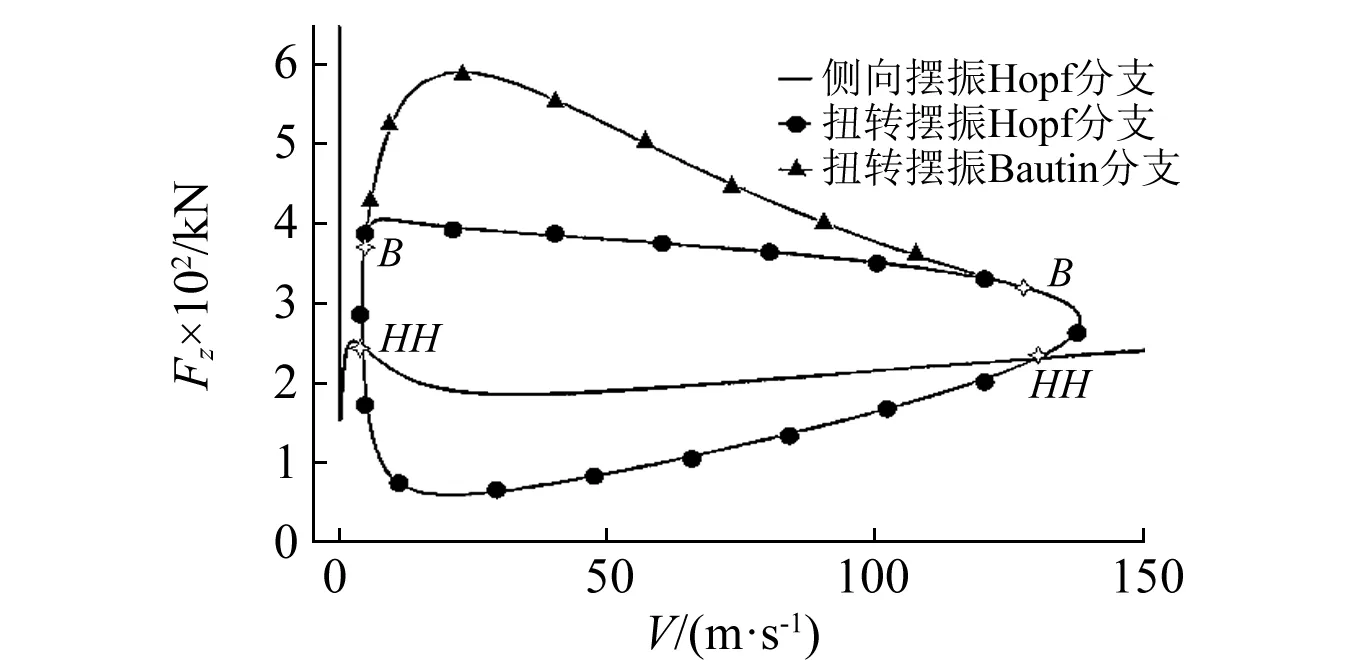
圖4 以垂向載荷、滑行速度為控制變量的分岔圖(2)Fig.3 Bifurcation map in vertical load-forward speed plane(2)

本章僅給出擺振分岔計算的基本流程，不給出分岔計算的具體理論[21]。

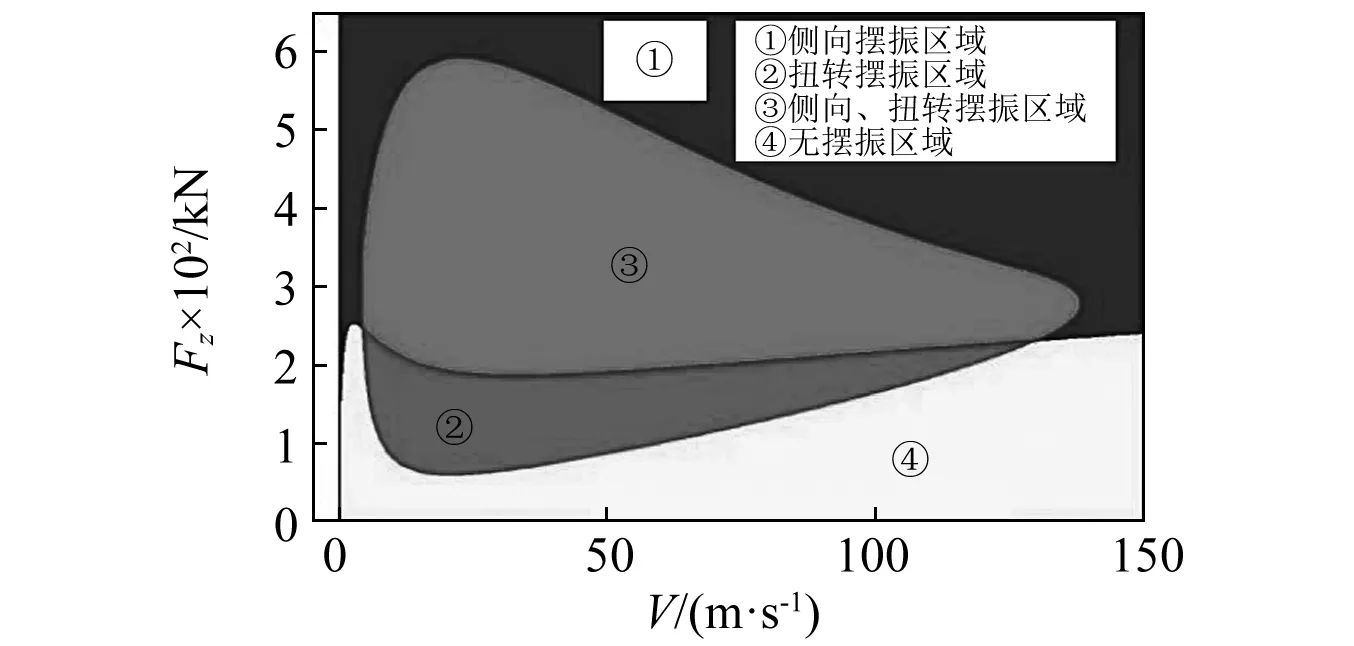
圖5 典型的擺振分岔圖Fig.5 Typical bifurcation map of shimmy analysis

3 擺振參數分析

3.1 輪間距對擺振穩定區的影響

圖6和圖7給出了輪間距D從0～0.4 m內不同取值的扭轉與側向擺振區域。

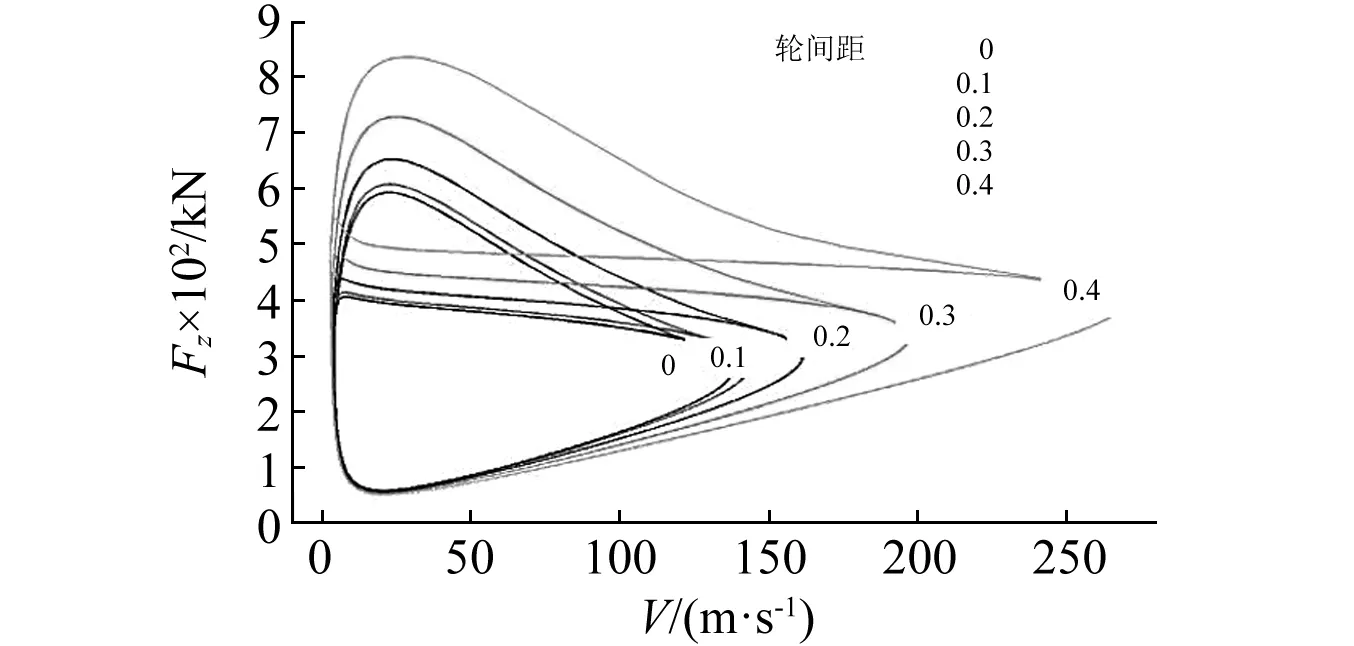
圖6 輪間距對扭轉擺振區域的影響Fig.6 Effect of tyre-distance on torsional shimmy bifurcation area

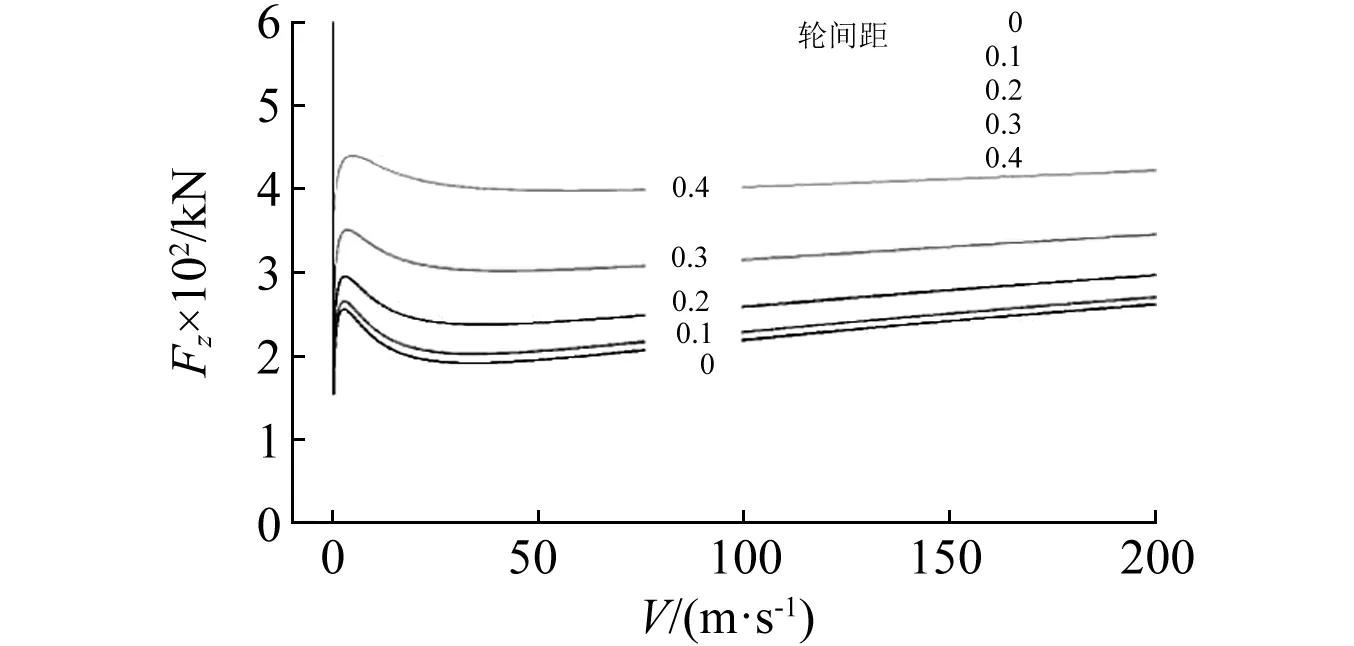
圖7 輪間距對扭轉擺振區域的影響Fig.7 Effect of tyre-distance on lateral shimmy bifurcation area

如圖6和圖7所示，隨著輪間距的增大，扭轉擺振區域產生了一定的增加，側向擺振區域則趨于減小。輪間距的增大，變相提高了支柱的側向彎曲剛度，進而對側向擺振起到抑制作用，對扭轉擺振則剛好相反。

除輪間距小于0.1 m時帶來的差異幾乎可以忽略外，輪間距變化導致擺振區域的差異是很明顯的。并且，輪間距其取值越大，其等幅增量引起的變化越為顯著。輪間距為0.4 m時的扭轉擺振區域面積是零輪間距情況的約2.5倍，側向擺振區域面積約為2倍。

在維持中低速和中低垂向載荷區域穩定性不變的同時，扭轉擺振區域隨著輪間距的增大，向高速高垂向載荷區域延伸擴展。側向擺振區域則向高垂向載荷區域拓展。

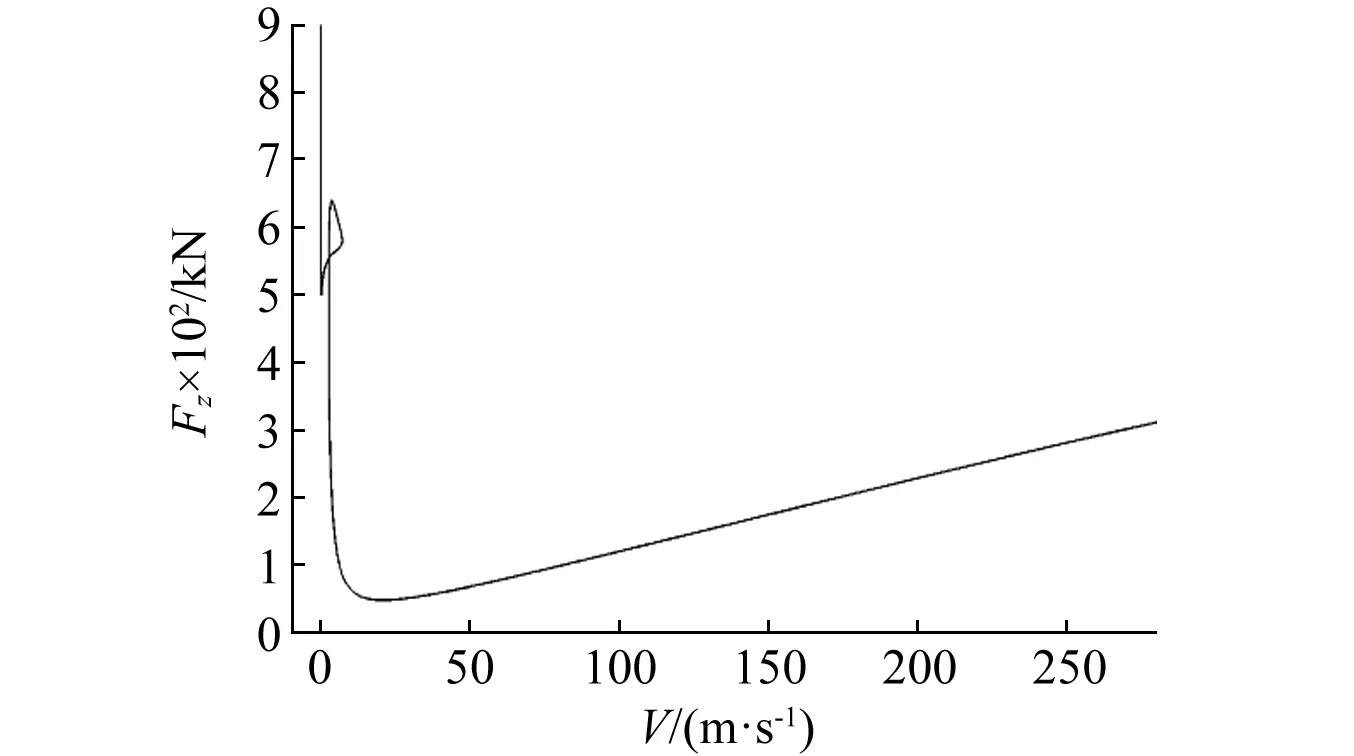
圖8 輪間距對擺振區域的影響Fig.8 Effect of tyre-distance on shimmy bifurcation area

圖8給出了輪間距為0.5 m時的擺振區域。相比不大于0.4 m的情況，其擺振區域截然不同。如圖8所示，輪間距為0.5 m的情況下，扭轉擺振與側向擺振的Hopf分支線完全融合。原有的兩組Hopf分岔曲線組成一條自相交的復雜曲線，表征了擺振的發生區域。在整條曲線的右上方，包含曲線左端的封閉區域，均會發生擺振現象。由于拓撲形式的改變，擺振類型無法嚴格地進行劃分。

3.2 雙輪共轉對擺振穩定區的影響

為綜合考察雙輪共轉對擺振區域的影響，計算輪間距分別為0.1 m，0.2 m和0.3 m時，采用雙輪共轉的擺振區域圖，與相應的不共轉情況進行對比，如圖9所示。

圖9 雙輪共轉對擺振穩定區的影響Fig.9 Effect of co-rotation wheels on shimmy bifurcation area

如圖9所示，在輪間距0.1 m的情況下，采取雙輪共轉的擺振穩定區與不共轉幾乎完全重合；隨著輪間距的逐漸增大，雙輪共轉一定程度上減小了高滑行速度下的扭轉擺振非穩定區，對于側向擺振區域則幾乎沒有影響。

4 結 論

本文建立了包含輪胎變形、支柱結構變形等自由度的雙輪起落架非線性擺振動力學模型，給出了一套采用分岔分析方法進行非線性擺振穩定性研究的方法，并對輪間距、雙輪共轉對擺振穩定性的影響進行了詳細分析。

(1)輪間距的增加變相提高了支柱的側向彎曲剛度，能減小側向擺振的發生區域，增大扭轉擺振區域。當輪間距超過某一臨界值時，輪間距會導致擺振區域拓撲結構的改變。

(2)采用雙輪共轉，對起落架的扭轉防擺在一定程度上起到積極的作用。在采用相對較大的輪間距時，雙輪共轉對扭轉擺振區域的影響更為明顯。對小輪距的起落架，雙輪共轉的作用是很有限的。