基于GM(1，1)模型的合肥市商品房房價預測

盛寶柱，古 鈴

(安徽建筑大學 經濟與管理學院，安徽 合肥 230601)

現實房價受許多因素的影響，如：GDP、城市人口數、人均可支配收入、土地供應價格、開發商投資額、銀行利率、房地產預期價格等，Gerlach、Peng就曾截取香港1982年1季度到2001年4季度的歷史數據，定量論證GDP、貨幣存儲量、房地產價格等變量之間的均衡與變化關系，得出銀行的信貸政策發生調整會導致房地產價格發生變化，且銀行貸款、房地產價格以及宏觀經濟間存在長期穩定關系的結論[1]。段軍山、白茜運用協整和VEC模型分析發現房地產價格的上漲會導致銀行貸款增加，短期內人均收入與銀行利率對房地產價格均呈現出正相關關系[2]。在房地產價格波動的研究中，黃礪、王佑輝運用HP濾波法對我國住宅地價的周期波動加以分析得出地價增長的周期性明顯且波動幅度日益增強的結論[3]。也有學者嘗試分析與房價波動關聯較大的因素，宋成舜、周惠萍就曾基于灰色系統理論分析西寧市商品房價格變化的主要影響因素，并取得了較好的分析效果[4]。一般用于房價預測的方法有很多，如：擬合預測模型、灰色系統理論、ARMA預測模型以及神經網絡模型等，吳璟、劉洪玉就利用灰色-馬爾可夫鏈模型對房地產價格波動進行剝離，用GM(1，1)模型預測長期趨勢因素，用馬爾科夫鏈模型預測短期波動因素[5]。閆鵬飛、王典、燕慧慧通過灰色理論原理，利用災變預測GM(1，1)模型預測出鄭州市商品房房價突變點[6]。近幾年間，孫波、劉瓊芳、王瑩等也分別運用灰色理論原理，以哈爾濱市、福州市、淮安市的房價數據為基礎建立GM(1，1)模型對房價走勢加以預測，都取得了很好的預測效果[7-9]。

以上研究都為我國各地區政府部門采取措施處理房價問題提供了富有價值的參考信息，但考慮到現有預測數據尚不能準確反映各省市的情況，需要對有關預測數據加以補充完善。因此本文以安徽省合肥市2005—2017年商品房均價的相關數據為基礎建立GM(1，1)預測模型，在驗證了模型精度的前提下對合肥市2018—2022年的房價走勢進行了預測。

1 研究方法與數據來源

1.1 研究方法

灰色系統理論經鄧聚龍教授首創以來，已經被廣泛應用于社會以及自然科學的諸多領域并取得了顯著的社會和經濟效益[10](P11)。

灰色系統理論的研究對象為部分信息已知，部分信息未知的“少數據”“貧信息”不確定性系統[10](P12)，主要通過對原始數據序列施加算子作用進行數據處理，得到規律性更為顯著的生成數據序列，再利用相關分析模型對生成數據序列的內在信息加以挖掘進而實現對未來趨勢的預測[10](P96)。目前灰色模型GM(1，1)模型的應用程度較高，該模型具有建模所需信息少，模型預測精度高等優點，因而相較于傳統預測方法顯示出極大的優越性，在經濟分析中被廣泛應用。

通過灰色系統理論可知，GM(1，1)具有一定的適用范圍：當發展系數-2<-α<2 時，GM(1，1)模型才有意義，且隨著α的取值不同，模型預測的精度也不相同。當|α|≥2時，GM(1，1)模型將不再有意義。

進一步探究可知，在GM(1，1)的有效范圍內，隨發展系數的增大，模型誤差也將迅速增加，當發展系數-α小于或等于0.3時，模型模擬精度可達98%以上；當發展系數小于或等于0.5時，模型模擬精度達到95%以上；當發展系數大于1時，模型模擬精度則將低于70%；當發展系數大于1.5時，模型模擬精度就將不足50%。由此可得以下結論：

1)當-α≤0.3時，GM(1，1)精度較高，能夠用于中長期預測；

2)當0.3<-α≤0.5時，GM(1，1)模型精度仍可滿足短期預測的要求，但對于中長期預測則需謹慎選擇；

3)當0.5<-α≤0.8時，GM(1，1)模型將不再適用于作短期預測；

4)當0.8<-α≤1時，應采用殘差修正的GM(1，1)模型；

5)當-α>1時，GM(1，1)模型精度不足70%，不再適用于數據預測[11](P145)。

1.2 數據來源

本文以合肥市2005—2017年的商品房實際交易數據為基礎建立GM(1，1)模型，在確定模型預測精度可靠的情況下，對2018—2022年的合肥市房價做出預測。

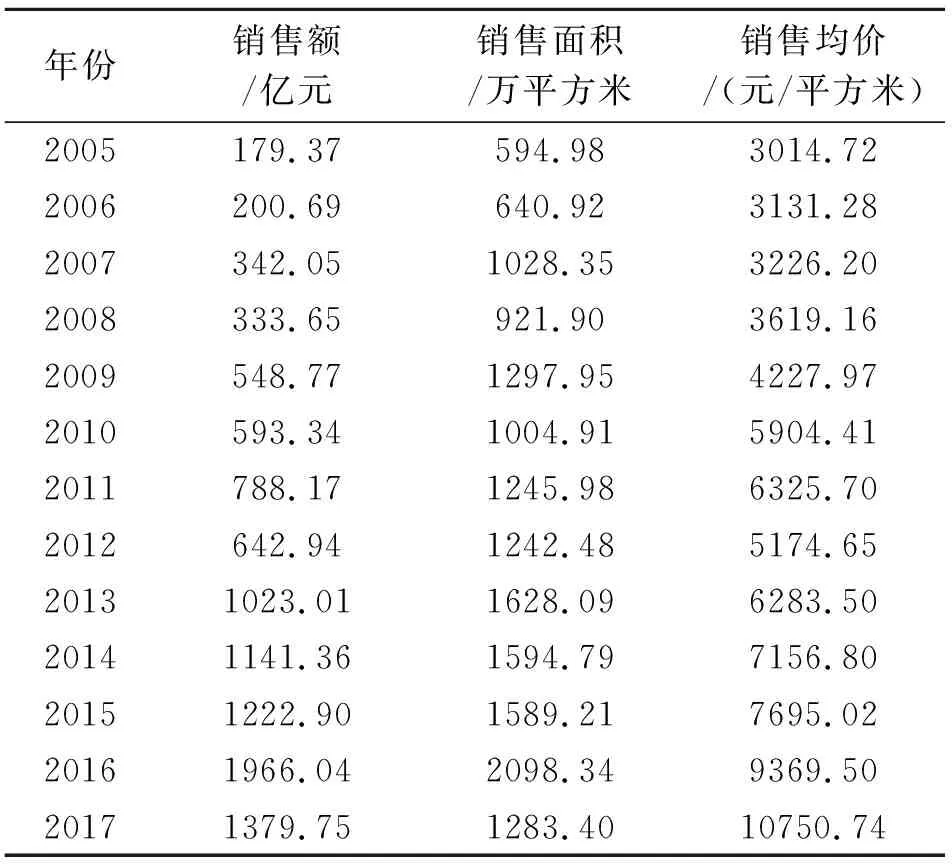
表1 2005年—2017年合肥市商品房銷售數據

數據來源：合肥市統計年鑒。其中銷售均價=銷售額/銷售面積。

2 GM(1，1)模型預測

2.1 GM(1，1)建模

首先，根據表1建立合肥市商品房銷售均價原始數據序列：

其中x(0)(k)≥0,k=1,2,…,13=(3015，3131，3226，3619，4228，5904，6326，5175，6284，7157，7695，9370，10751)。

2.1.1 數據處理

為消除原始數據的隨機性和波動性，建立原始序列X(0)的1-AGO序列：

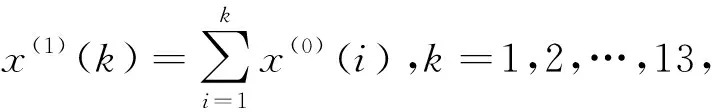
建立X(1)的緊鄰均值生成序列：

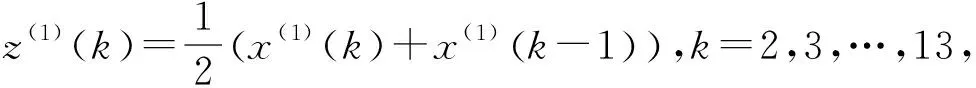
2.1.2 參數估計

建立差分方程：

相應的白化微分方程為：

(1)

構造數據矩陣B和數據向量Y：

可得：

其中-α為發展系數，反映X(0)與X(1)的發展態勢；β為灰色作用量。根據2.1節內容所述，本例-α=0.1083<0.3，因此所建立的GM(1，1)模型可用于中長期預測。

解方程(1)可得：

2.2 模型誤差檢驗

解得GM(1，1)模型參數后可應用模型對原始數據進行預測得到2005—2017年合肥市商品房的預測均價，該數據可用于模型的檢驗。

商品房實際均價與預測均價的走勢對比如圖1所示。

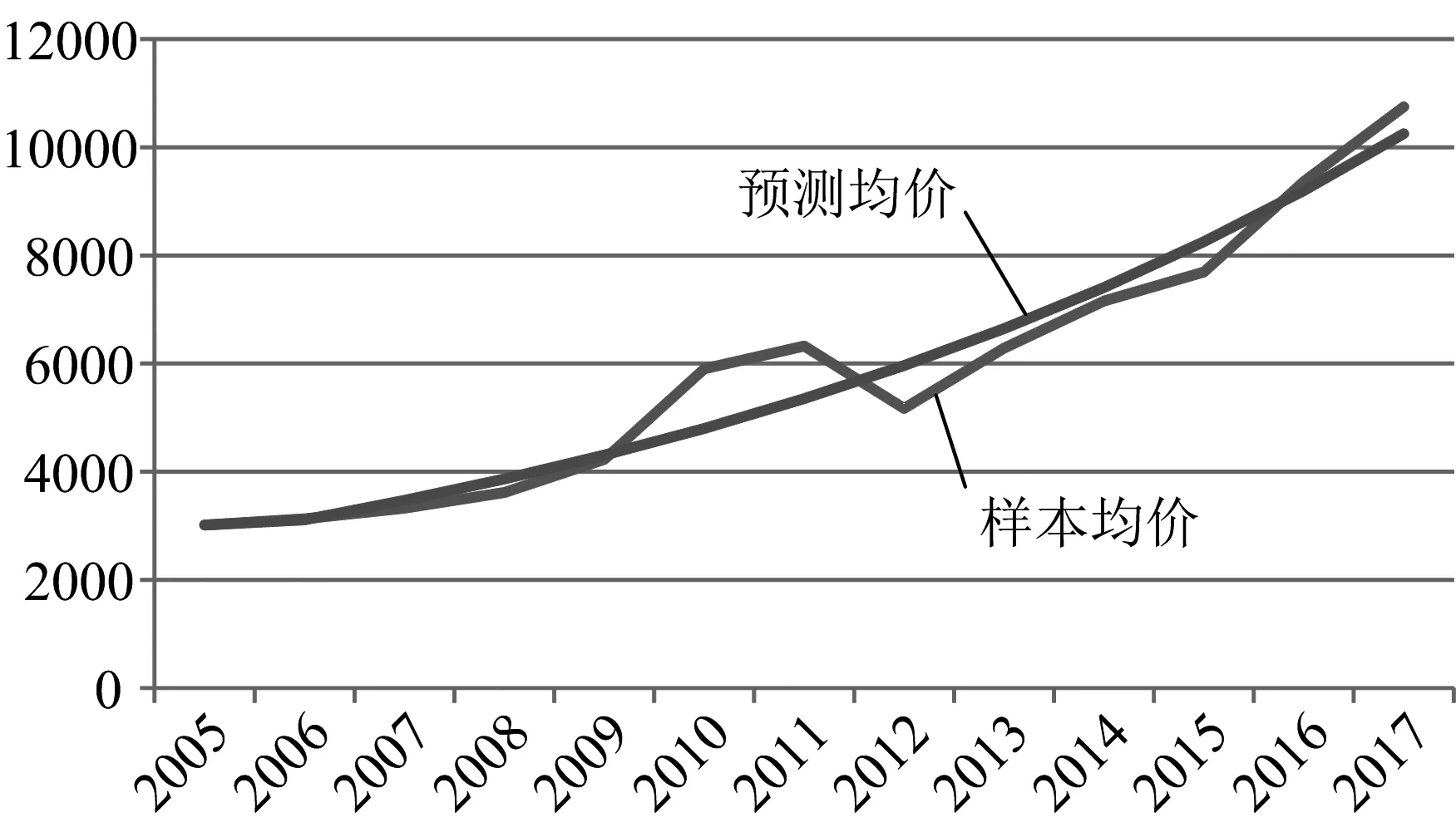
圖1 實際數據與預測數據對比圖

從走勢對比圖中可以看出二者均呈同樣的上升趨勢。預測均價與樣本實際均價相比變化更為平緩，可以看作是實際數據在序列算子作用下減弱隨機擾動，強化內在規律性后得到的數據序列，在經過檢驗確定該預測模型所得預測值達到所需精度后，即可應用預測值作其他進一步的房價分析。

為確保GM(1，1)的模擬預測值具有可信度，一般需要對模型進行誤差檢驗，主要有以下指標：相對誤差、平均相對誤差、關聯度、均方差比值、小誤差概率等。

2.2.1 相對誤差

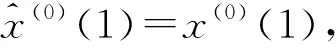
再用所得殘差計算相對誤差序列：

計算得到相對誤差序列為：

最后用所得相對誤差序列計算平均相對誤差：

計算得到平均相對誤差為：

根據平均相對誤差的精度等級劃分：平均相對誤差為0.01時的精度等級為一級；平均相對誤差為0.05時的精度等級為二級；平均相對誤差為0.1時的精度等級為三級；平均相對誤差為0.2時的精度等級為四級。結合計算得到的平均相對誤差可知：模型的平均相對誤差精度等級約為二級。

2.2.2 關聯度

先計算關聯系數序列：

其中ρ為分辨系數，是在區間(0，1)內取得的實數，一般取ρ=0.5。

(2)脫介篩上物料不能過厚，否則會嚴重影響脫介效果；磁選機處理能力必須充足;在操作過程中，一旦發現磁選機有翻花現象，磁選尾礦中就有可能帶介較高；建議在以后的設計、建設中，充分考慮煤質變化情況，配備足夠的介質回收設備。

計算得到關聯系數序列為：

根據所得關聯系數序列計算關聯度：

計算得到關聯度為：

根據關聯度精度等級劃分：關聯度為0.9時其精度等級為一級；關聯度為0.8時的精度等級為二級；關聯度為0.7時的精度等級為三級；關聯度為0.6時精度等級為四級。結合計算得到的關聯度可知：模型的關聯度等級約為四級。

結合2.2中的預測數據與樣本數據對比圖可以看出：2010年，2011年以及2012年的商品房實際均價呈現出較大幅度的波動：2010年數據的殘差為1101.174，2011年數據的殘差為974.22，2012年數據的殘差為-789.182。進而使得樣本數據與預測數據關聯度下降。這主要是受到當年的房地產調控政策、土地供應情況、銀行利率等因素的影響，根據資料顯示，2011年央行共進行了3次加息，6次上調存款準備金率，出臺的嚴厲限制性政策對民眾的購房需求造成了打擊，因此過去近13年間的數據中，2012年銷售均價較2011年是唯一一次出現了下降的。

2.2.3 均方差比值

計算原始序列均值：

方差：

計算殘差序列均值：

方差：

最后計算均方差比值：

計算得到均方差比值為：

根據均方差比值的精度等級劃分：均方差比值為0.35時其精度等級為一級；均方差比值為0.5時的精度等級為二級；均方差比值為0.65時的精度等級為三級；均方差比值為0.8時精度等級為四級。結合計算得到的均方差比值可知達到了一級精度。

2.2.4 小誤差概率

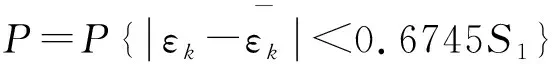
P=1.

根據小誤差概率的精度等級劃分：小誤差概率為0.95時其精度等級為一級；小誤差概率為0.8時的精度等級為二級；小誤差概率為0.7時的精度等級為三級；小誤差概率為0.6時精度等級為四級。結合計算得到的小誤差概率可知精度等級為一級。

預測值的各項指標檢驗結果如表2所示。

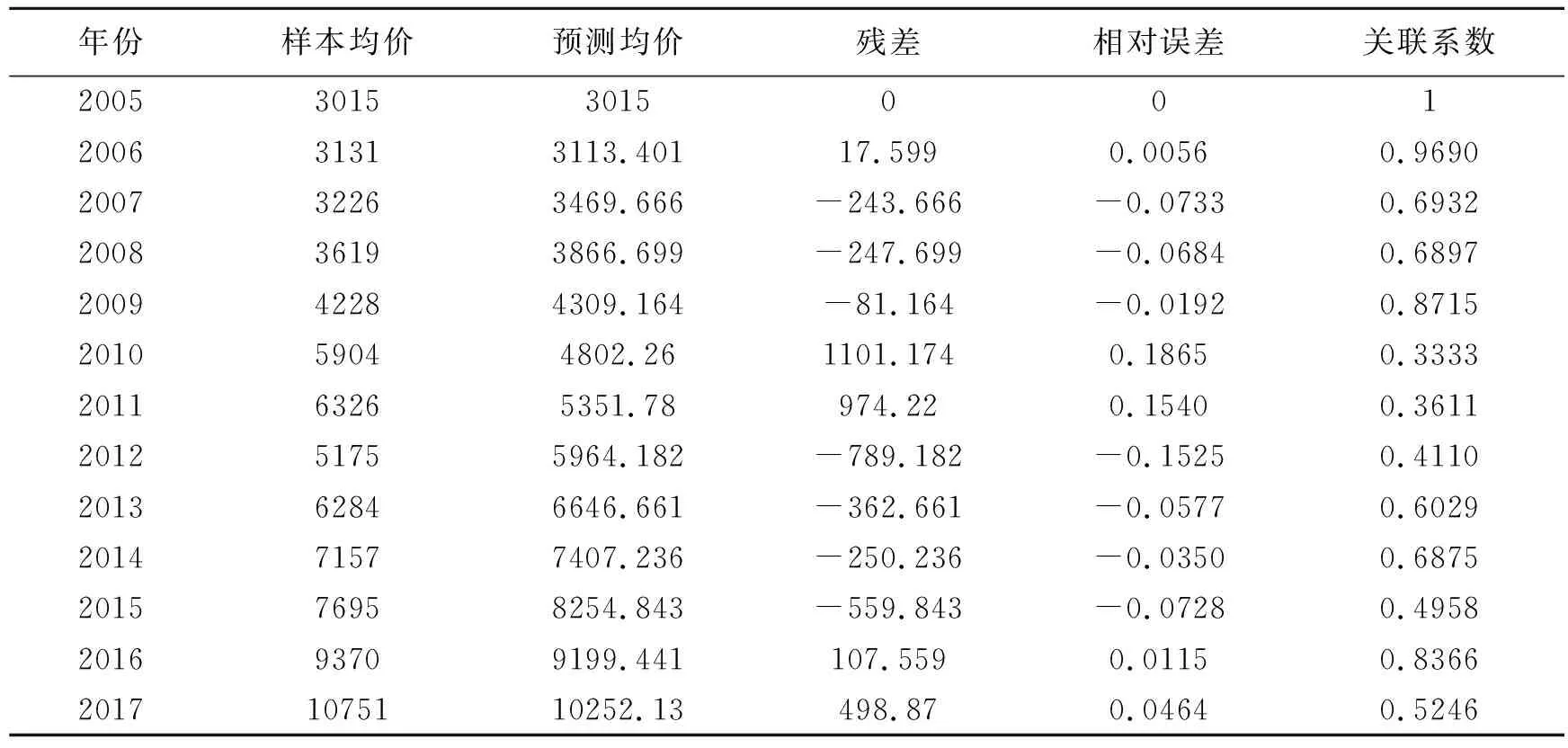
表2 預測均價檢驗

綜上可知，模型整體的平均相對誤差精度等級約為二級；關聯度等級約為四級；均方差比值精度等級為一級；小誤差概率精度等級為一級，因此模型整體運行結果可信。

3 未來房價走勢預測

經檢驗，本文以合肥市2005—2017年商品房實際交易數據為基礎建立的GM(1，1)模型精度可靠，可用于未來房價預測，現針對2018—2022年的合肥市房價走勢做出預測，結果如表3所示。

表3 2018—2022年合肥市商品房房價預測

4 結論

從歷史數據來看，合肥市商品房房價在2012年有過小幅回落，主要是受當年土地資源供應情況以及政府出臺的限價措施影響，但總體來看仍呈現上漲趨勢。通過模型做出的短期預測數據可以看出：合肥市房價在未來仍具有上升規律。未來五年間合肥市商品房房價都將以每年約11.44%的速度增長，其中，2018年房價預計將比2017年增長6.27%。合肥市作為安徽省省會，地處我國華東、江淮地區間，氣候適宜，同時又是皖江城市帶的核心城市，具有極大的發展潛力，因此房地產價格的增長是發展的必然，但同時也應該看到，住房作為人們生活的剛需，房價的過快增長對于合肥市的人才引進和人口擴大等都是不利的，尤其合肥作為國家重要的科研教育基地，對于人才的需求十分旺盛。

根據歷史數據，政府的一系列抑制房價的舉措發揮出了一定的作用，而對于合肥未來五年的房地產市場變化，政府有必要加大對房地產市場的監管力度，規范市場秩序，嚴厲打擊炒房行為，平衡房地產市場的供求關系，合理抑制過高地價，從而從根本上保證房價不會過快增長。