數學課堂實踐活動的課程優化策略

吉俊

摘 要：數學課堂實踐活動不僅屬于數學教學，更應納入數學課程的范疇。作為教師，要以全新的理念，從課堂實踐活動的目標、內容、過程與評價等方面進行優化，促進學生數學課堂實踐活動的開展。通過實踐活動課程的優化，提升學生的數學學力，發展學生的數學素養。

關鍵詞：課堂教學；實踐活動；活動課程；優化策略

“現代課程理論之父”托爾夫·泰勒在《課程與教學的基本原理》一書中提出這樣的課程觀點：課程目標、課程內容、教學過程與教學評價影響著教師對整個教學活動體系的認識與理解。在數學課堂實踐活動中，許多教師在活動組織、安排、設計與開展等方面花費時間多，但成效卻微乎其微，甚至感到無所適從。如何提升學生數學課堂實踐活動水平，使之成為一種課程？筆者認為，依循托爾夫·泰勒的課程理論，對數學課堂實踐活動要素進行整體優化，能夠實現數學實踐活動向數學課程的轉化。

一、活動目標：從知能轉向情意

數學課堂實踐活動是培養學生創新思維的有效途徑。探究性是數學課堂實踐活動的基本特性。因此，數學課堂實踐活動的目標就不能僅僅定位于獲得某種知識和技能，而應向學生情感、態度和價值觀領域延伸。從知能型目標轉向情意型目標，能夠激發學生數學學習的好奇心、求知欲，讓學生從被動接受轉向主動探索。

例如：教學《比的意義》這一課，在學生理解了比的意義以及求比值的方法后，筆者將學生帶到學校升旗臺旁，設計這樣的實踐活動課題：請同學們想一想，如何測量出學校旗桿的高度？學生聽到這一話題都很感興趣，爭先恐后地發表自己的見解和主張。有的說，可以將旗桿放下來，此話一出便立即遭到其他學生的一致否定；有學生說，可以用旗桿的定滑輪將卷尺拉到頂端進行測量，但其他學生卻反駁說，這樣測量容易產生較大誤差。這時，筆者啟發學生可以運用所學數學知識解決問題，學生之間展開了積極交流。有學生認為，可以用一根米尺和旗桿放在太陽光下，然后根據旗桿、米尺、桿影和尺影間的關系，運用“比的知識”解決問題，此法得到學生的普遍贊同；還有學生想出了這樣的辦法：將國旗的旗桿和米尺平行放置，用手機從正面拍攝下來，根據圖片中旗桿和米尺的圖像間的比的關系，算出國旗旗桿的高度，這一方法也得到了學生的普遍認同。此時，學生都迫不及待地想去拍攝、測量。于是筆者趁熱打鐵，給學生提供了所需要的測量、拍攝工具，讓學生自主展開實踐活動，學生自然而然地進入親身體驗的問題解決情境之中。

數學課堂實踐活動既能提高學生學習興趣，又能讓學生在愉悅的實踐活動中增長知識，教學效果事半功倍，學生的數學創新意識和能力也得到了相應的激發和培育。數學課堂實踐活動目標從知能轉向情意，數學課堂實踐活動由簡單告知學生怎樣測量轉變為學生通過討論、交流形成各種活動方案，通過彼此合作進行嘗試。在這個過程中，學生通過活動形成正確的情意態度，活動指向學生數學素養的發展和提升。

二、活動內容：從固化轉向選擇

內容選擇是數學課堂實踐活動有效開展的關鍵。傳統的數學活動，其內容往往是教材預設的，或者是教師欽定的，學生只是被動地執行。數學課堂實踐活動，必須讓每一位學生參與進來，因此，活動內容的選擇就倍顯重要。學生不只是數學課堂實踐活動的開展者，更是數學課堂實踐活動內容的設計者、開發者。數學活動內容要從固化轉向選擇，使其更貼合學生的生活實際。

比如，教學《三角形、平行四邊形和梯形》后，筆者以《圖形的密鋪》為主題，讓學生進行數學課堂實踐活動。活動以小組為單位，由學生自主選擇研究圖形，然后在平板電腦上復制、拖動、旋轉、組合，由此構筑了一個學生自主參與、體驗的活動舞臺。學生發現，圓形不能密鋪，因為圓是一個曲線圖形。那么，是否正多邊形都能密鋪呢？學生發現，正五邊形不能密鋪。那么，怎樣的正多邊形能密鋪呢？不同活動內容的活動小組產生了共同的疑問，他們之間展開了小組交流、討論。接著，密鋪正三角形、正方形、正六邊形等幾個小組的學生形成了這樣的猜想：一個正多邊形，如果能夠通過旋轉，圍繞公共頂點形成一個周角，這個正多邊形就能密鋪。通過對正八邊形、正十邊形等圖形的驗證，學生發現，這些正多邊形都不能密鋪。因為正六邊形的一個內角是120°，而從正七邊形開始，它們的內角都大于120°而小于180°，所以都不能鋪成360°的周角，都不可以密鋪。由此，學生形成更一般、更為深度的活動探索，即怎樣的圖形能夠密鋪？學生再次選擇活動內容，分小組展開探索。有小組探索一般的平行四邊形，通過平移、旋轉發現能夠密鋪；有小組探索一般的三角形，還有小組探索一般的四邊形，通過活動，探索出圖形密鋪的奧秘。

教師提供給學生圖形密鋪素材，讓學生展開自主操作、觀察、猜想、推理與驗證等活動，學生積極動手、動腦、動口。學生因困激思、因惑啟智，在提出問題、分析問題和解決問題的過程中不斷積累豐富的數學活動經驗，逐步逼近數學知識的本質，其數學思維水平從感性上升為理性，從具象提升為抽象。

三、活動過程：從組織轉向分享

華中師范大學郭元祥教授認為，“作為一種實踐取向和經驗取向的課程，實踐活動比其他任何形式的課程都更加注重過程的教育價值”。傳統的數學課堂實踐活動的開展往往是組織指導型的，這樣的組織指導盡管能讓課堂實踐活動順利地進行下去，但卻降低了活動的育人價值。在數學課堂實踐活動中，教師應始終以學生為主體，努力通過學生的活動體驗、獨立思考，積極參與其中，讓課堂實踐活動從組織轉向分享。在這個過程中，教師要發揮“點穴式作用”，學生能夠自行思考、探究的，教師不提示，學生思考、探究有困難的，教師精巧點撥，以此助推學生課堂實踐活動。

比如，教學《怎樣滾得遠》，我們在活動中將科學老師邀入課堂，將科學課和數學課進行整合，拓展數學課堂實踐活動的時空。活動采用小組合作的方式，借鑒科學中的對比實驗，控制一個變量，也就是斜面與地面的夾角，讓學生進行數學實踐活動。活動前，有學生猜想斜面與地面的夾角越大，膠帶圈滾得越遠；有學生猜想斜面與地面的夾角越小，膠帶圈滾得遠；還有學生猜想45°時膠帶圈滾得遠……據此，筆者給學生提供了實驗器材，學生分別選取了30°、45°和60°進行實驗。他們各負其責，有的用木板和磚塊搭斜坡，有的用量角器量斜面夾角，有的讓膠帶圈自然滾下去，還有的拉長卷尺進行測量。分工不分家，學生在課堂實踐活動中相互提醒，彼此分享著活動經驗。在實驗中，有小組學生認為，不能僅僅憑借3個斜面夾角就下定結論，而應該再選取一些夾角。于是，學生分小組再一次展開實驗，有小組用45°夾角和比30°小的夾角進行比較，有小組用45°夾角和比60°大的夾角進行比較……這樣的數學課堂實踐活動，學生收獲的不僅是數學知識，更是豐富的數學活動經驗、深刻的數學思想方法和嚴謹的科學研究態度。

數學課堂實踐活動，需要教師預留一定的自主時空。如此，學生才能通過實踐活動來形成團隊合作意識、分享交流意識等。學生在活動中形成一種相互啟發、相互促進、相互學習的嶄新探究樣態。通過活動，學生形成自我認同，更形成了與他人分享交流的積極心態。

四、活動評價：從診斷轉向發展

美國著名教育評價專家布盧姆認為：“教育必須日益關心所有兒童與青年的最充分的發展。”傳統的數學活動評價，其弊病是明顯的，一是教師單向度評價；二是偏重結果性評價；三是評價關注活動的外在形式，而忽視學生在活動中的內化與發展。換言之，這樣的活動評價是一種診斷性評價，缺乏評價的導向、激勵性作用。優化課堂實踐活動評價，要求評價主體多元化、評價方式多樣化、評價過程多向化等，將評價貫穿于數學課堂實踐活動的始終。

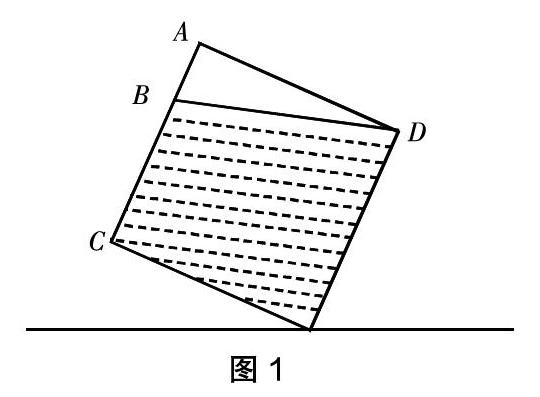
例如：在教學《正反比例的意義》后，筆者出示了這樣一道習題：小明在一個內側（從里面量）棱長為2分米的正方體容器內裝滿水，然后將容器傾斜放置（如圖1），流出來的水恰好是1升。試求出線段BC與線段AB長度的比是多少？

初次遇到這樣的問題，學生不知所措。于是，筆者找來一個正方體容器，讓學生將容器灌滿水，然后將容器傾斜，學生通過課堂實踐活動發現，無論怎樣傾斜，水面始終經過正方體的頂點D點。筆者適時激勵啟發學生，“圖中空白部分的面積和陰影部分的面積與什么有關？”“正方體的高一定，正方體的體積與正方體的底面積成什么比例？”在教師的點撥下，有學生恍然大悟：原來高一定，空白部分的面積與陰影部分的面積的比就是倒出水的體積與剩下水的體積的比。由此，學生求出了空白部分的面積與陰影部分的面積分別是0.5平方分米和3.5平方分米。這時，學生又遭遇了新的困難。有學生正要泄氣，同小組的學生卻相互激勵、相互啟發——“別泄氣，我們一定有辦法。”“剛才已將倒出水與剩下水的體積比轉化成面積比，那我們能再將面積比轉化成長度比嗎？”“三角形和梯形是不同的圖形，如果能轉化成相同的就好了。”在思維的相互激蕩中，學生過B點作了一條與AD平行的線段，問題的解決變得敞亮開來。正方形的一條邊一定，線段BC與線段AB之間的長度比被轉化成面積比，由此學生自主解決問題。

優化活動目標、內容、過程與評價，是提升數學課堂實踐活動有效性的基本策略。作為教師，要以全新的理念指導教學，創設條件，促進學生數學課堂實踐活動的展開，讓數學課堂實踐活動真正指向學生數學素養的生成，指向學生數學學力的發展，讓學生“動有所樂”“樂有所思”“思有所悟”。