正推逆證思路在初中數學幾何中的應用

杜會利

摘 要：隨著新課標改革的不斷推進，數學教學要求逐漸加深。數學在實際生活中應用比較廣泛，初中數學教學具有十分重要的地位。初中數學中的幾何題型貫穿整個教學階段。但是由于其對學生的空間思維和邏輯分析能力要求較高，很多學生在進行學習的過程中并不能夠很好地把握，就使得逐漸淡化了了學習的興趣，造成數學科目整體的成績較差。在本文中，筆者就憑借自己多年的初中數學教學經驗，談一談正推逆證思路在初中數學幾何中的應用。

關鍵詞：正推逆證；初中數學；幾何教學；應用

正推思路我們比較容易理解，就是根據題目中所提供的有效條件來對其進行相應的推理，最終得出問題答案的過程。而逆向思路都與大多數學生來說比較難以掌握和理解，其實逆向思路也叫做求異思維，就是對人們常生活中習以為常或者早已經成為定論的事物或者觀點進行反向思考的一個思維過程，敢于對一個問題反其道而行之，從思維過程的對立面來對其進行相應的探索，樹立起一個新思想，創立起一個新過程。

一、初中幾何教學的實際現狀

在初中教學的實際過程之中，幾何教學一直是困擾著學生學習的重大阻礙，它不僅要求學生有著較強的數學計算能力，而且還對學生的空間想象能力有著較高要求，這樣就會使得學生在具體的學習過程中顯得十分的吃力。而且大多數老師對于幾何教學的教學模式都是采取“填鴨式”的教學模式，老師在上面講學生在下面被動的接受，不能夠進行良好的師生互動，這樣就使得學生自己對于知識內容的探索不能夠更加的深入，時間長了就會慢慢喪失對于幾何內容的學習興趣。所以老師在進行幾何內容的實際教學過程中，要特別注意知識的傳授方式和學生對于知識的接受情況，采取合理的教學模式來滿足學生對于知識的渴求，進而切實提高學生對于幾何數學的學習能力。

二、借助幾何圖形，進行合理的猜想

在處理幾何題目的過程之中，大多數題型是可以通過正推方法來進行解決的，因為很多題目的信息都蘊含在幾何圖形之中，比如長度、形狀、位置等等。如果學生能夠很好的發掘其中所蘊含的有效信息，并將其中的關系有效地串聯起來，通過合理的猜想假設，就可以很好地找到解決題目的思路，來進行相關的證明解決。

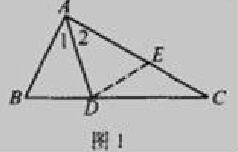
例：如圖1所示。在△ABC中，∠B=2∠C，AD是∠A的角平分線。求證AB+BD=AC。對于這種題型來說，多采取正推法來解決。

如果在AC上截取AE=AB，這樣就只需求證BD=EC即可，而結合AD是∠A的平分線，利用三角形全等的相關定理，以及三角形外角是內角的關系進行合理的猜想，就能夠很輕松的得出解題思路。

證明 如圖所示，在AC上截取AE=AB，

由于AD是∠A的角平分線，即∠1=∠2，

又因為AE=AB，AD為公共邊，

所以根據全等定理，△BAD≌△EAD，

所以BD=DE，∠B=∠AED，

又因為∠AED=∠C+∠EDC，∠B=2∠C，

所以∠C=∠EDC，所以EC=ED

所以EC=BD，

所以AB+BD=AE+EC=AC

總結：在大多數的幾何題目圖形之中，題目之中或者圖形內所蘊含的已知條件是很多的，雖然大部分已知條件看起來是沒有關聯的，所以這就需要學生們進行具體的思索，尋找它們之間的聯系。

三、利用逆向思維模式，進行幾何問題的相應解決

利用逆向思維的解題方式，將傳統的解題思路顛倒過來，由未知問題去推導已知條件，這種新穎的解題方式能夠給學生帶來更多的學習興趣，進而能夠更加全身心地投入到幾何問題的學習過程中。

在當今人教版的幾何內容過程過程之中，首先引入的是學生比較熟悉的線段內容，在平行線之中要求學生進行一些簡單的推理，利用逆向思維的推導方式，能夠對于問題進行一個更好的解決。

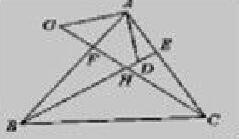
例如，如圖所示，在△ABC中，BE，CF分別是AC，AB兩邊上的高，在BE上截取BD=AC，在CF上的延長線上截取CG=AB，連接AD，AD。

求證：（1）AD=AG。

（2）AD與AG的關系如何。

分析：（1）要證AD=AG→△ABD≌△AGC→∠ABD=∠ACG→∠FHB=∠EHC→CF⊥AB（已知條件）；AB=GC（已知條件）；BE⊥AC（已知條件）；AG=AD（已知條件）。

（2）由（1）可知，∠AGC=∠BAD→∠AGC+∠GAF=90°→∠DAG=90°→AD⊥AG。

通過這種逆向思維的推理方法，學生對于幾何問題的分析就會有著更好的理解，相應的在這種題型中就會花費更少的時間。而且這種逆向思維的推理模式不僅能夠運用于幾何題型之中，對于其他的數學問題也能夠很好的解決，這樣對于學生學習數學也是一個很好的幫助。

總而言之，在進行實際問題的解決過程中，也需要通過一些相應的邏輯思維模式來進行具體的解題步驟，所以這就要求老師在實際的教學過程中能夠把握好幾何推理過程的相應特點，進行相應思維模式的講解，從而使得學生能夠更好地掌握這些內容的知識點，完成實際的教學目標。

參考文獻：

[1]范成.初中數學幾何推理與圖形證明策略例談[J].數理化解題研究（初中版），2014（10）.

[2]胡敏華.淺析逆向思維在初中數學中的應用[J].讀書文摘，2014，03.