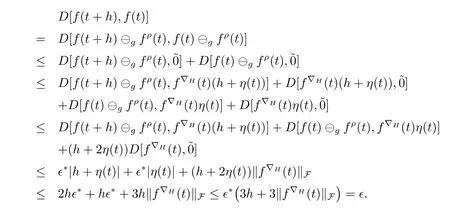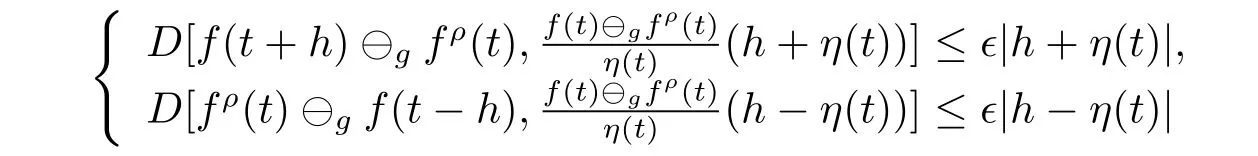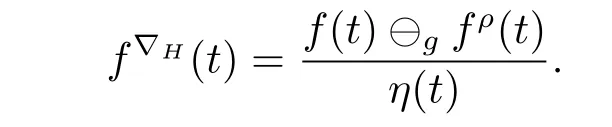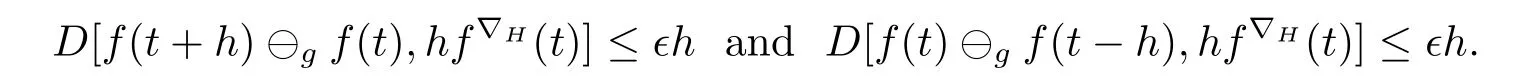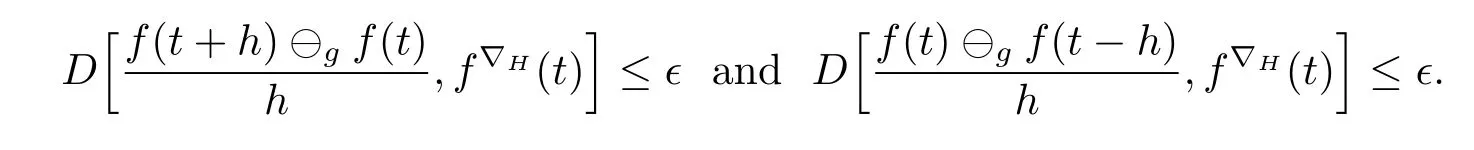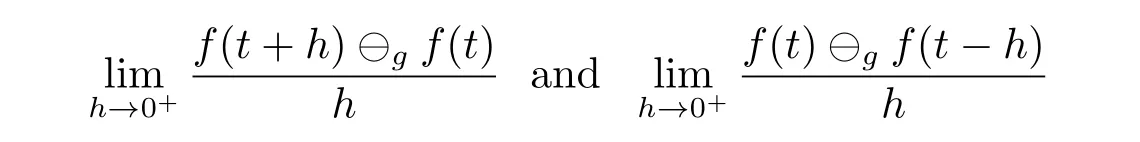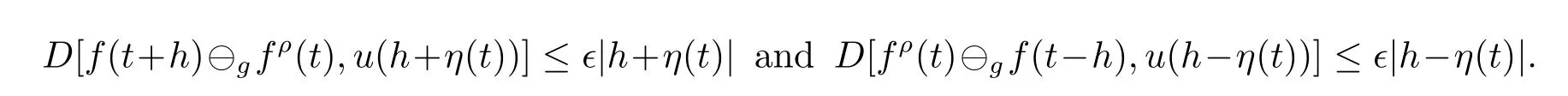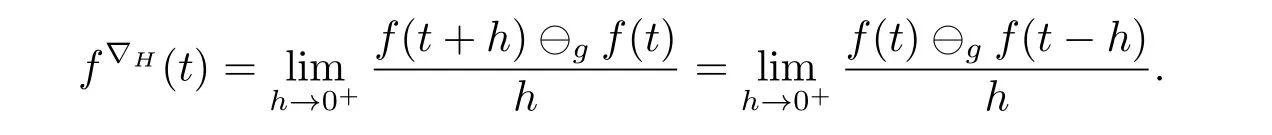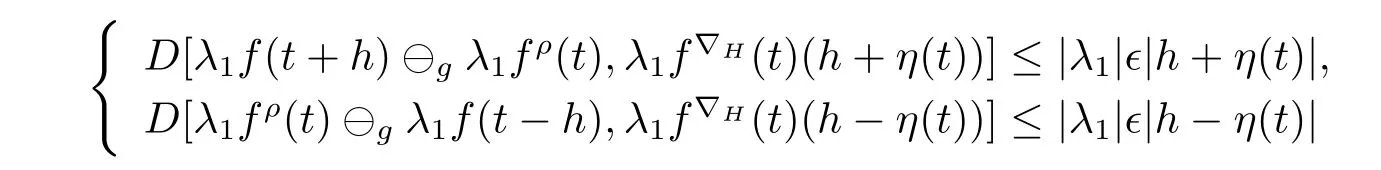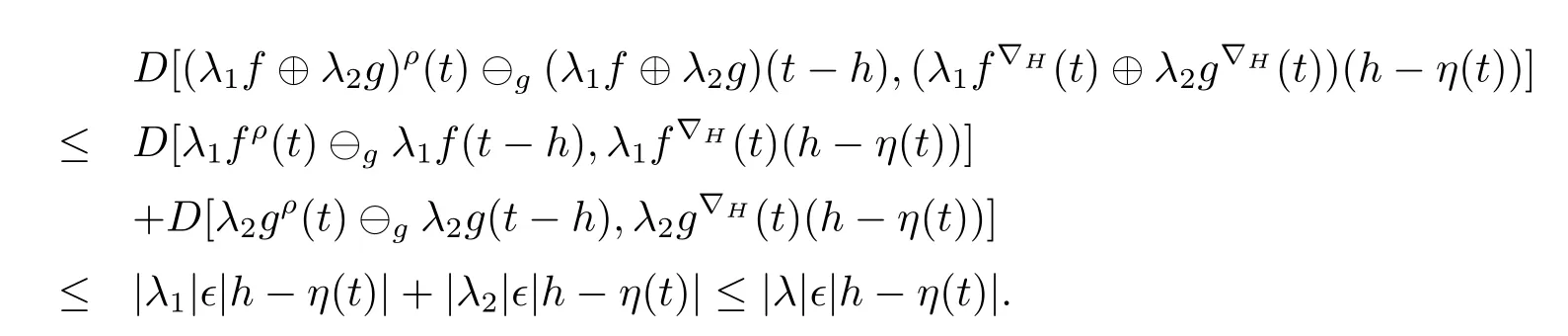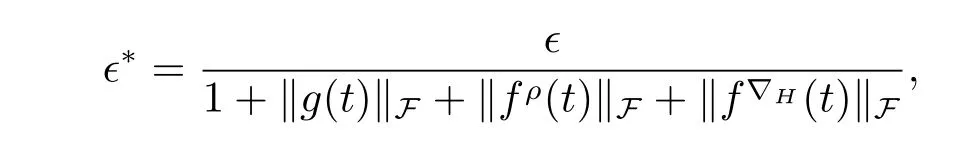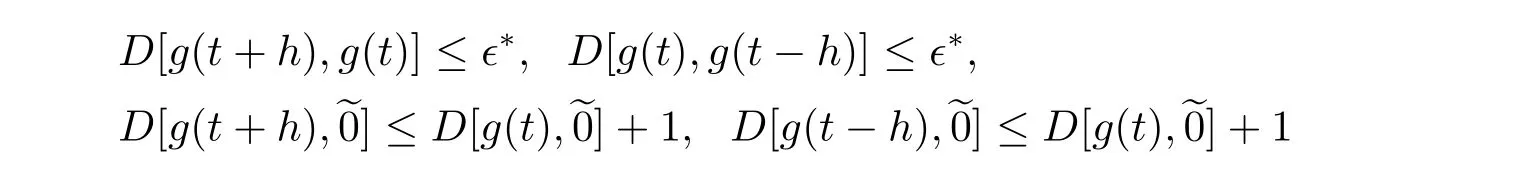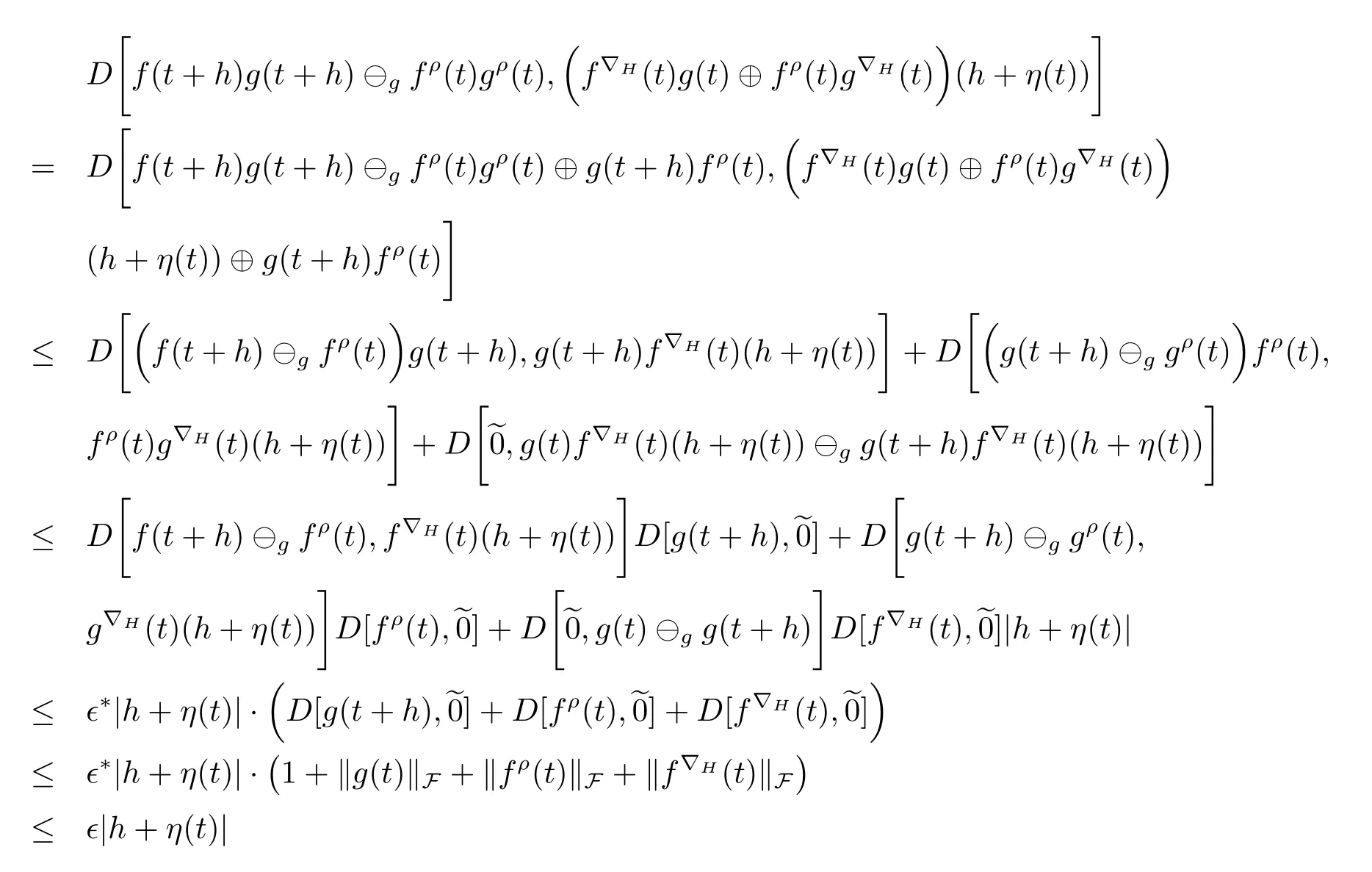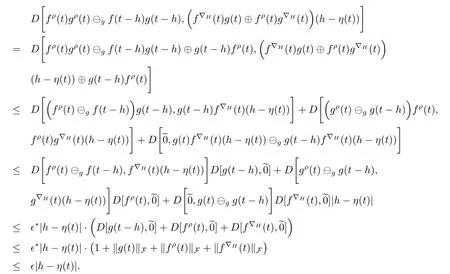NABLA-HUKUHARA DERIVATIVE OF FUZZY-VALUED FUNCTIONS ON TIME SCALES

YOU Xue-xiao,ZHAO Da-fang,LI Bi-wen

(School of Mathematics and Statistics,Hubei Normal University,Huangshi 435002,China)

Abstract:In this paper,we introduce and investigate the concept of Nabla-Hukuhara derivative of fuzzy-valued functions on time scales.By using the theory of time scales,we show some basic properties of the Nabla-Hukuhara derivative,which extend and improve the related ones in[12].

Keywords:Nabla-Hukuhara derivative;fuzzy-valued functions;time scales

1 Introduction

The Hukuhara derivative was the starting point for the topic of set differential equations and later also for fuzzy differential equations.But the Hukuhara derivative in FDE suffers certain disadvantages(see[3])related to the properties of the space Knof all nonempty compact sets of Rnand in particular to the fact that Minkowski addition does not possess an inverse subtraction.To overcome this obstacle,several generalized fuzzy derivative concepts were studied from different viewpoints by some authors[4–8].

Recently,the authors in[9]introduced the concept of fuzzy derivative for fuzzy-valued functions on time scales,which provides a natural extension of the Hukuhara derivative.In this paper,we define the Nabla-Hukuhara derivative of fuzzy-valued functions on time scales,which gives another type of generalization of the Hukuhara derivative.We also show some basic properties of the Nabla-Hukuhara derivative.Results obtained in this paper extend and improve the related ones in[12].

2 Preliminaries

In this section,we recall some basic definitions,notation,properties and results on fuzzy sets and the time scale calculus,which are used throughout the paper.Let us denote by RFthe class of fuzzy subsets of the reals u:R→[0,1],satisfying the following properties

(1)u is normal,i.e.,there exists x0∈R with u(x0)=1;

(2)u is a convex fuzzy set,i.e.,for all x1,x2∈R,λ∈(0,1),we have

(3)u is upper semi-continuous;

As a distance between fuzzy numbers,we use the Hausdor ffmetric defined by

for u,v∈RF.Then(RF,D)is a complete metric space.

A time scale T is a nonempty closed subset of R with the subspace topology inherited from the standard topology on R.For t∈ T,we define the forward jump operator σ(t)by σ(t)=inf{s>t:s ∈ T}where inf? =sup{T},while the backward jump operator ρ(t)is defined by ρ(t)=sup{st,we say that t is right-scattered,while if ρ(t)

Definition 2.1[7]A function f:[a,b]→RFis said to be left differentiable at t if there exist A and δ>0,such that

(1)f(t)?f(t?h)exists for 0

(2)f(t?h)?f(t)exists for 0

The element A is said to be the left derivative of f at t,noted as(t).

Definition 2.2[7]A function f:[a,b]→RFis said to be right differentiable at t if there exist A and δ>0,such that

(1)f(t+h)?f(t)exists for 0

(2)f(t)?f(t+h)exists for 0

The element A is said to be the right derivative of f at t,noted as(t).

Definition 2.3[7]A function f:[a,b]→RFis said to be differentiable at t if f is both left and right differentiable at t,and(t)=(t).The element(t)or(t)is said to be the derivative of f at t,denoted as f′(t).

3 Nabla-Hukuhara Derivative

Definition 3.1 Assume that f:T→RFis a fuzzy function and let t∈Tk.Then we define f?H(t)to be the number(provided that it exists)with the property that given any ?>0,there exists a neighborhood U of t(i.e.,U=(t? δ,t+ δ)∩ T for some δ>0)such that

for all t?h,t+h∈U with 0≤h<δ.

We call f?H(t)the Nabla-Hukuhara derivative(?H-derivative for short)at t.Moreover,we say that f is?H-differentiable on Tkprovided that f?H(t)exists for all t∈ Tk.The fuzzy function f?H(t):Tk→RFis then called the?H-derivative on Tk.

Some useful properties of the?H-derivative of f are given in the next theorem.

Theorem 3.2 Let f:T→RFand t∈Tk.Then we have the following.

(i)Function f has at most one?H-derivative at t.

(ii)If f is?H-differentiable at t,then f is continuous at t.

(iii)If f is continuous at t and t is left-scattered,then f is?H-differentiable at t with

(iv)If t is left-dense,then f is?H-differentiable at t if and only if the limitsandexist as a finite number and are equal.In this case,

(v)If f is?H-differentiable,then f(t)=fρ(t)⊕ f?H(t)η(t).

Proof(i)The proof is easy and will be omitted.

(ii)Assume that f is ?H-differentiable at t.Let ?∈ (0,1).Denote

Then ??∈ (0,1),here we have for u ∈ RF,D[u,]= ∥u∥Fwith ?0,a zero element of RF.By Definition 3.1 there exists a neighborhood U of t such that

for all t?h,t+h ∈ U.Therefore,for all t?h,t+h ∈ U ∩(t? ??,t+??)we have

Similarly,we can prove that D[f(t),f(t? h)]< ?.Therefore,f is continuous at t.

(iii)Assume that f is continuous at t and t is left-scattered.By the continuity,

for all t?h,t+h∈U.It follows that

for all t?h,t+h∈U.Hence we get the desired result

(iv)Assume that f is ?H-differentiable at t and t is left-dense.Then for each ?>0,there exists a neighborhood U of t such that

for all t? h,t+h ∈ U.Since ρ(t)=t,η(t)=0,we have that

It follows that

Hence we get the desired result

On the other hand,if the limits

exist as a finite number and are equal to u ∈ RF,then for each ?>0,there exists a neighborhood U of t such that

for all t?h,t+h∈U.

Since t is left-dense,we have

Hence f is?H-differentiable at t and

(v)If t is a left-dense point,then ρ(t)=t,η(t)=0 and we have

If t is left-scattered,then by(iii),we have f(t)=fρ(t)⊕ f?H(t)η(t),and the proof of part(v)is completed.

Now,we present two examples to show that the Nabla-Hukuhara derivative is more general than the generalized derivative proposed in[7].

Example 3.3 We consider the two cases T=R and T=Z.

(i)If T=R,then f:R→RFis?H-differentiable at t if and only if the limits

exist as a finite number and are equal.In this case,

If T=[a,b],the Nabla-Hukuhara derivative reduces to the generalized derivative proposed in[7].

(ii)If T=Z,then f:Z→RFis?H-differentiable at t with

Example 3.4 If f:T→RFis defined by f(t)=[0,t2]for all t∈T:={:n∈N0},then from Theorem 3.2(ii),we have that f is?H-differentiable at t with

Theorem 3.5 Assume that f,g:T→RFare?H-differentiable at t∈Tk.Then

(i)for any constants λ1,λ2,the sum(λ1f⊕λ2g):T → RFis?H-differentiable at t with

(ii)if f and g are continuous,then the product fg:T→RFis?H-differentiable at t with

Proof(i)Since f and g are?H-differentiable at t∈ Tk,for any ?>0,there exist neighborhoods U1and U2of t with

for all t?h,t+h∈U1with 0≤h<δ1,and

for all t?h,t+h∈U2with 0≤h<δ2.

Let U=U1∩ U2,δ=min{δ1,δ2},λ =max{λ1,λ2}.Then we have,for all t∈ U,

and

Therefore(λ1f⊕λ2g)is?H-differentiable with

(ii)Let 0

then 0

for all t?h,t+h∈U1with 0≤h<δ1,and

for all t?h,t+h∈U2with 0≤h<δ2,and there exists neighborhoods U3of t such that

for all t?h,t+h∈U3with 0≤h<δ3.

Let U=U1∩ U2∩ U3,δ=min{δ1,δ2,δ3}.Then

for all t?h,t+h∈U with 0≤h<δ.We also have

Thus(fg)?H(t)=f?H(t)g(t)⊕fρ(t)g?H(t).

The other product rule formula follows by interchanging the roles of functions f and g.

Conclusions This paper investigate the Nabla-Hukuhara derivative of fuzzy-valued functions on time scales,which extends and improve the related ones in[12].Another research is to investigate the Nabla-Hukuhara derivative of fuzzy-valued functions on time scales in other different directions rather than the one considered here.For instance,instead of following the Nabla approach that we adopt,one can develop a diamond,or a symmetric Hukuhara derivative.These problems will be subject of future research.