具有反饋控制和時滯的隨機logistic種群模型的均值穩定性與滅絕性
戴祥軍,毛 志,徐松金
(銅仁學院大數據學院,貴州銅仁 554300)
1 引言
生物種群模型主要是用來描述、調節、控制和預測每個物種的發展過程和發展趨勢,從而對一些生態問題和自然生命現象做出合理的決策和方案,其中Logistic種群系統作為最基本的一類生物數學模型,已經被廣大學者所研究.1993年,Gopalsamy和Weng考慮到物種在其生存的環境中可能會受到負反饋的影響,譬如有毒的剩余殘渣的積累,人為的控制調節等.同時考慮到種群的密度變化和種群生命運行規律活動的演化過程不是瞬時發生的,而是有一定的時間延遲的;大量事實也表明許多事物的變化規律不僅依賴于當前的狀態,還與過去的歷史有關,即受時間滯后的影響.于是提出了如下一類具有反饋控制的logistic模型[1]
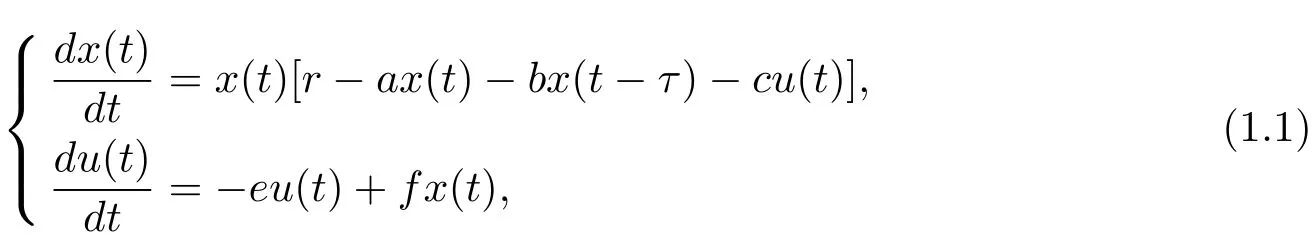
其中x(t)是種群在t時刻的種群密度,u(t)是反饋控制變量;r表示內凜增長率;a,b表示同種群的競爭系數,且r,a,b,c,e,f為正常數.他們探討該系統平衡點的全局漸近穩定性等性態.近年來,具有反饋控制的種群系統受到廣大學者的關注[2?5].
然而,在現實環境中,種群不可避免的會受到環境中各種細小的隨機因子的干擾,如某天突然下場雨、溫度突然升高等等,捕食者與食餌的隨機相遇等,這些細小的隨機因子可以綜合看成是白噪聲的作用.因此環境白噪聲對種群的影響是不可忽視的且考慮白噪聲的干擾將更加有實際意義.目前已經引起了廣大學者的高度重視[6?8].Mao[6]指出環境白噪聲的干擾可能會影響出生率,死亡率和競爭系數等其他參數.在這里假設環境白噪聲主要影響系統(1)的增長率r.而我們通常估計一個值都是通過它的平均值加上它的誤差項,即r→r+σ˙B(t),其中˙B(t)代表白噪聲,而σ2代表白噪聲的濃度,σ≥0.B(t)是定義在完備概率空間(?,F,P)上的布朗運動,且B(0)=0.因此在系統(1.1)的基礎上提出如下一類具有反饋控制和時滯的隨機logistic種群模型
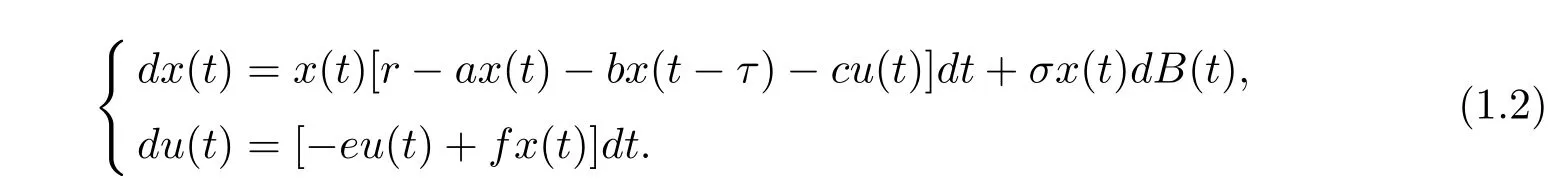
令初始條件為
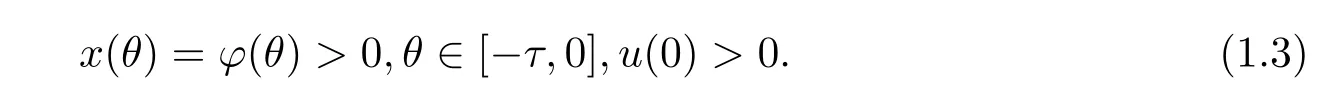
對于具有反饋控制的隨機種群模型的研究成果還很少,因此在這里也沒有太多的文獻可以借鑒.為了方便起見,給出了下列記號
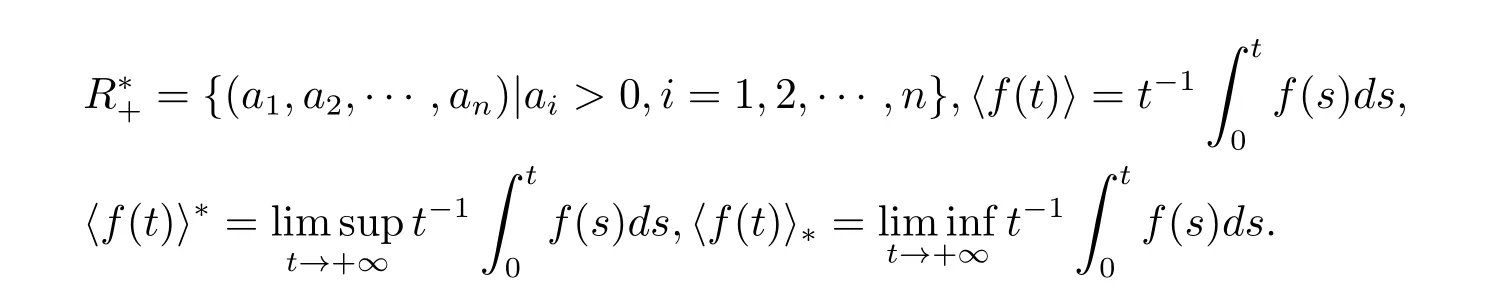
2 全局正解
因為x(t)代表種群的密度,那么它應該是非負的.因此首先就是討論系統(1.2)存在唯一全局正解.
定理2.1 對任意給定的正初始值滿足條件(1.3),系統(1.2)存在唯一全局正解(x(t),u(t))(t≥?τ),且此解以概率1停留在R+內.
證 因為系統(1.2)的系數滿足局部Lipschitz條件,那么對于任意給定的正初始值滿足條件(1.3),存在唯一的局部解(x(t),u(t))在[?τ,τe),其中τe是爆破時間.
為了去證明系統(1.2)的解是全局正解,那么只要證明τe=∞.設n0>0充分大,使得初始值落入區間[1/n0,n0],對于每一個正整數n>n0,定義停時
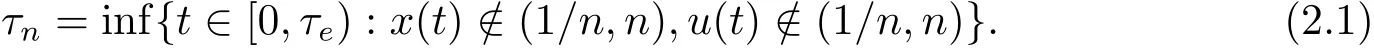
顯然 τn隨著n→ +∞ 是遞增的,設因此 τ∞≤ τe. 所以只需要證明τ∞=+∞.使用反證法,如果結論是錯的,那么這里一定存在常數T>0和ε∈(0,1),使得P(τ∞
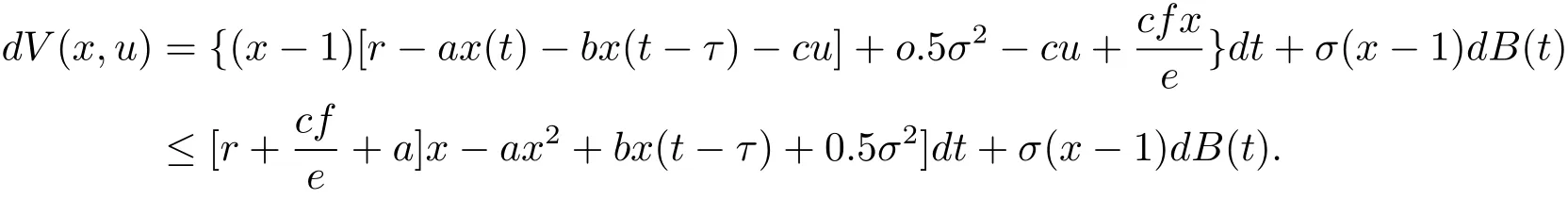
上式從0到τn∧T積分再取均值有
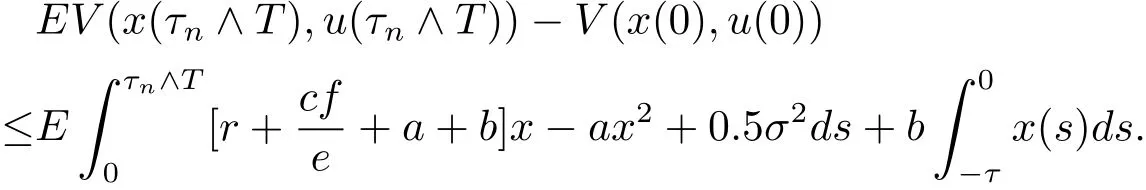
很容易知道一定會存在正常數K,有
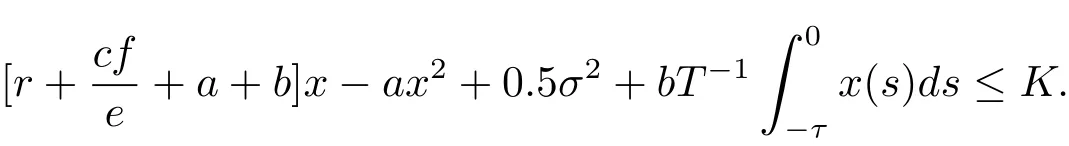
則

由于剩下的證明跟文獻[7]的證明類似,在這里就省略了.
3 均值穩定性與滅絕性
本節主要是探討系統(1.2)解的均值穩定性與滅絕性.首先先介紹幾個引理.
引理 3.1[8]假設Z(t,ω)∈ C(R+,?).
(1)如果存在正常數μ和T,使得對任意的t≥T,有
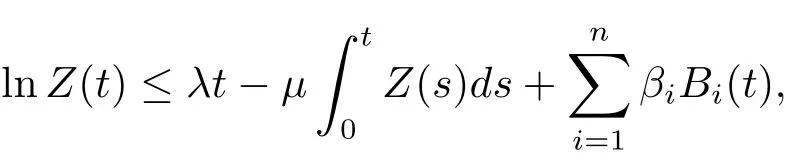
那么
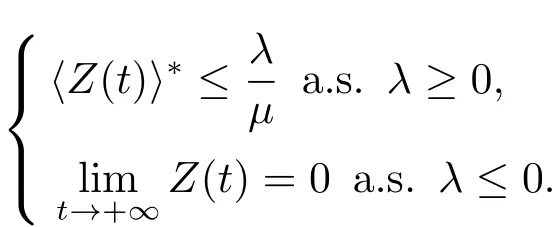
(2)如果存在正常數λ,μ和T,使得對任意的t≥T,有
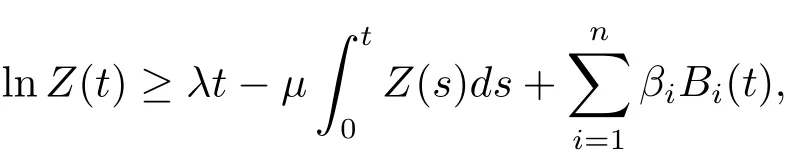
那么 ?Z(t)??≥a.s.
引理3.2[9]考慮隨機微分方程dx=x[r?ax]dt+σxdB(t),其中r,a,σ為正常數.當r>0.5σ2時,對于任意的初始值x0>0,方程的解x有
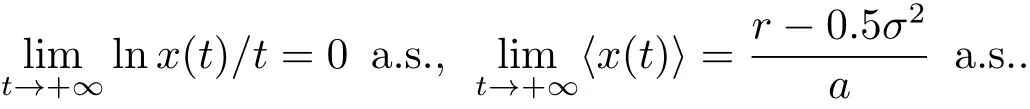
定理3.1當r≠0.5σ2時,對任意初始值滿足(1.3),則系統(1.2)有
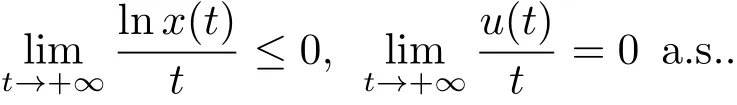
證 由系統(1.2)顯然有dx≤x[r?ax]dt+σxdB(t).
設X(t)是下面這個隨機微分方程的解
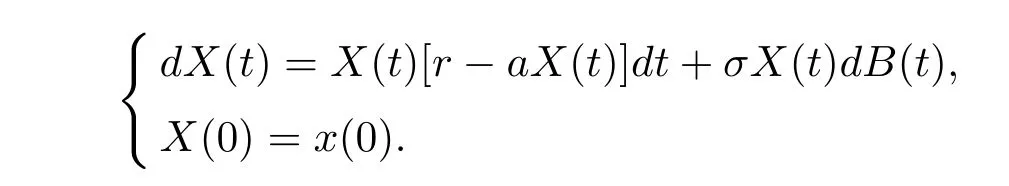
上式方程有如下復雜的顯式解
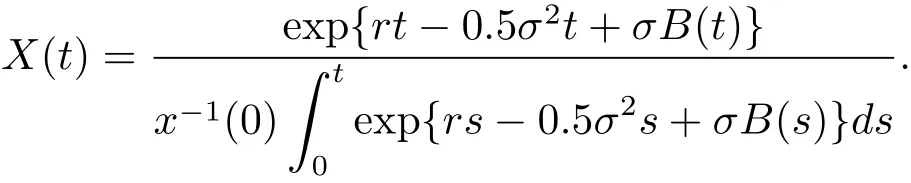
同樣根據方程(1.2)的第二個方程有
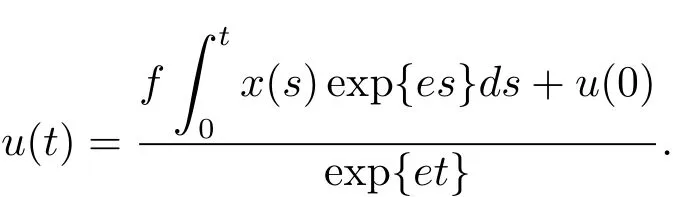
如果r<0.5σ2,由比較原理可知
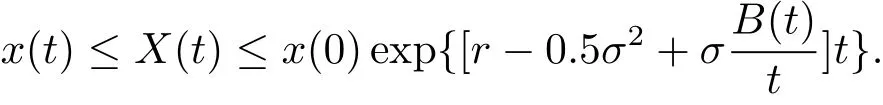
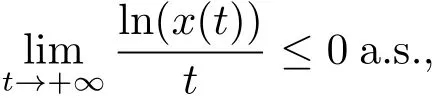
如果 r>0.5σ2,那么
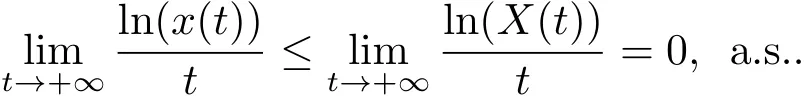
對exp{et}lnX(t)應用伊藤公式,

然后兩邊同時在[0,t]上積分再除以texp{et}有
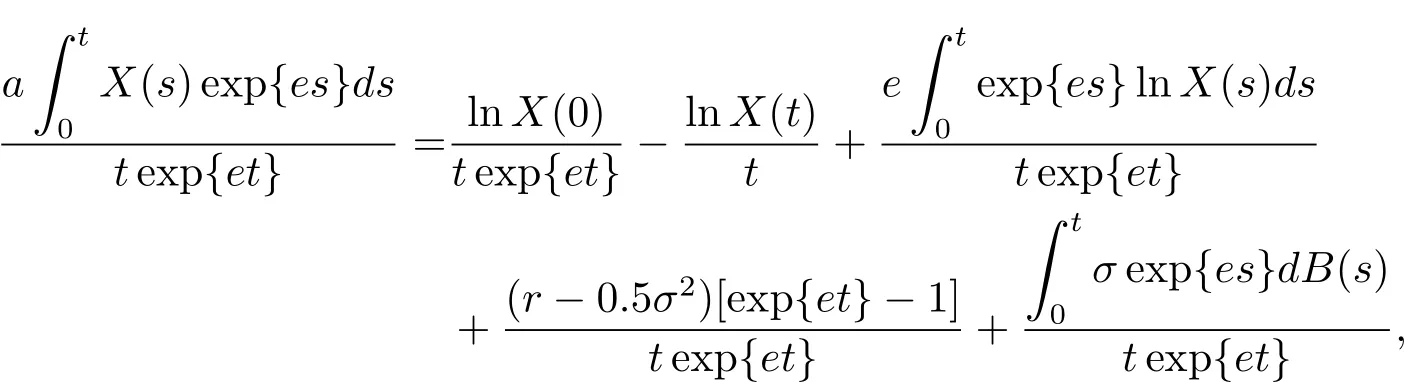
那么根據積分中值定理有
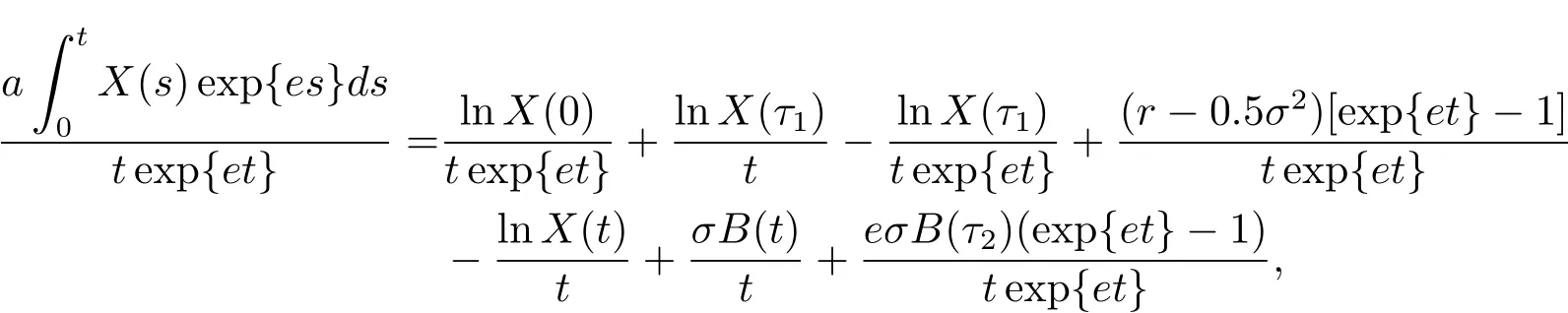
其中τ1,τ2∈[0,t].由引理3.2和=0,有
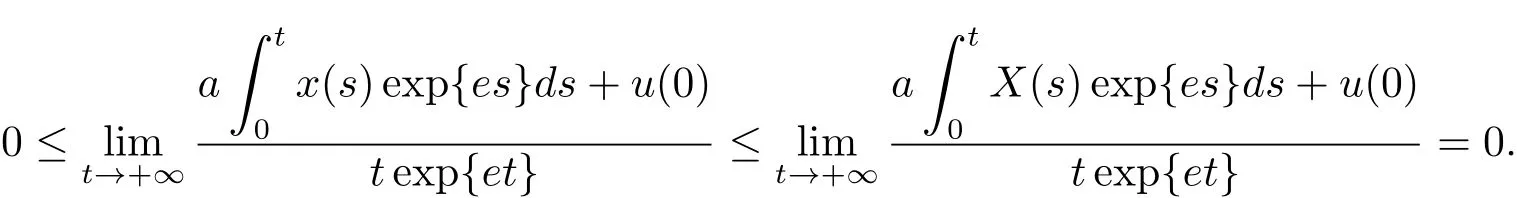
定理3.2 對于任意初始值滿足條件(1.3),
(1)如果r?0.5σ2<0,那么種群x(t)將趨于滅絕.即
(2)如果r?0.5σ2>0,那么種群x(t)均值穩定.即
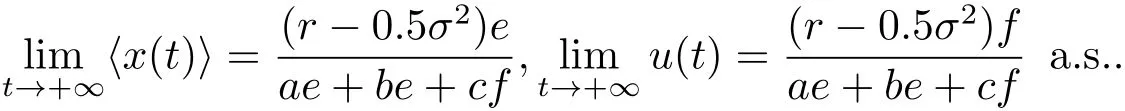
證 對(1.2)式應用伊藤公式,有
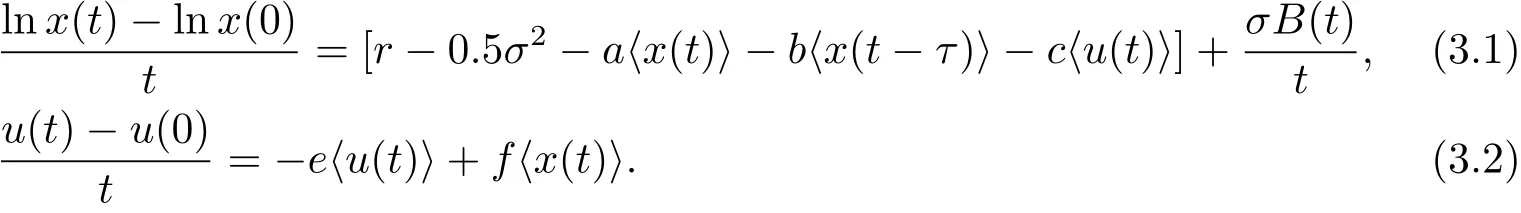
由(3.1)式可知
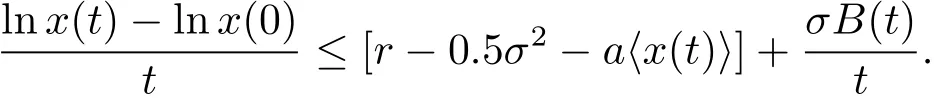
(1)當r?0.5σ2<0時,根據引理3.1可知
(2)當r?0.5σ2>0時,由(3.1)式可知
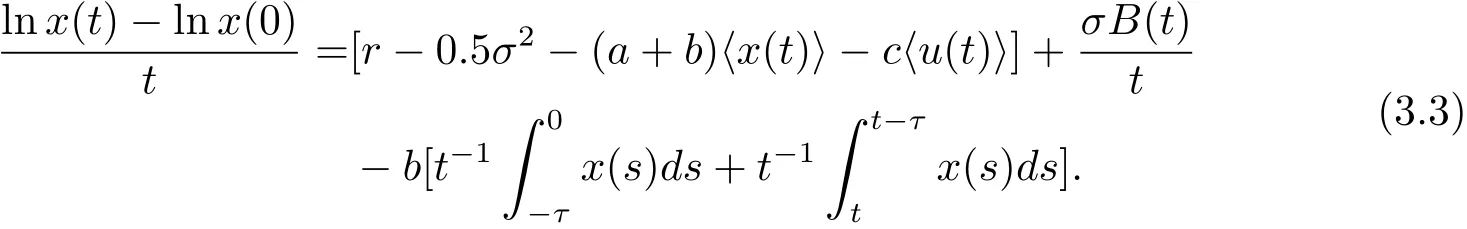
根據引理3.2可得
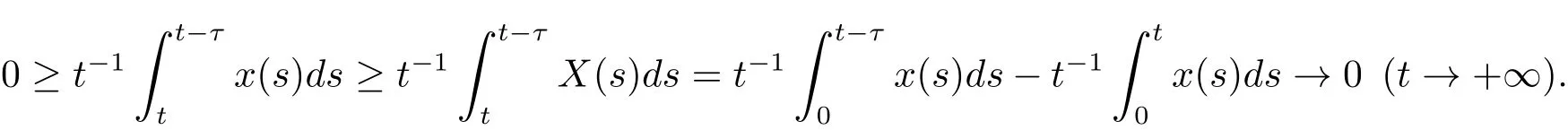
因此對于ε>0,假設ε足夠的小,使得r?0.5σ2?ε>0,存在常數T>0,當t≥T時,有
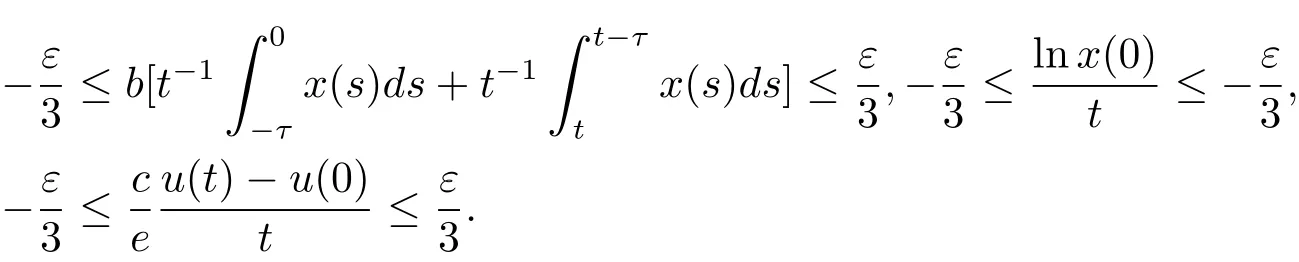
把上面不等式代入等式(3.1)和(3.2)可得
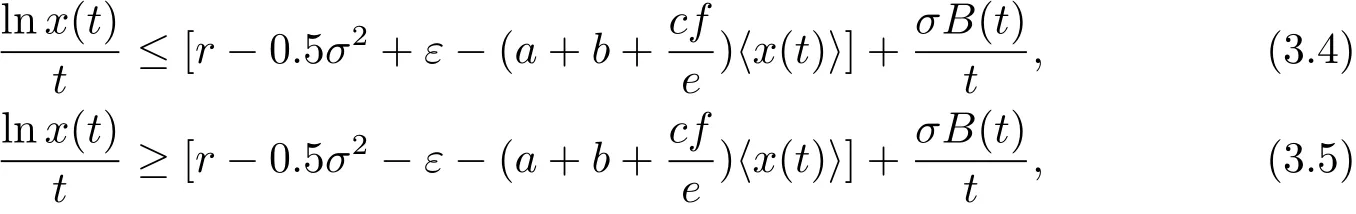
那么由(3.4),(3.5)式和引理3.1可知
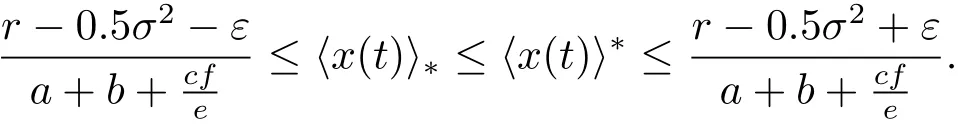
由ε的任意性可知
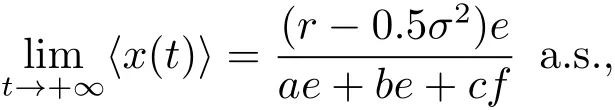
故
完成證明.
4 一般情況
上一節已經討論了一類具有反饋控制和時滯的logistic種群模型的均值穩定性和滅絕性.現在把它推廣到更一般的情形,考慮n個相互競爭種群,同樣我們考慮環境白噪聲的干擾,在這里假設種群可能同時受到n個獨立的白噪聲源的影響,假設白噪聲主要影響種群的增長率,因此采用下面這種擾動形式,如文獻[10],即其中σij≥ 0.
下面就來考慮一類具有反饋控制的n個種群的隨機Lotka-Valterra競爭系統
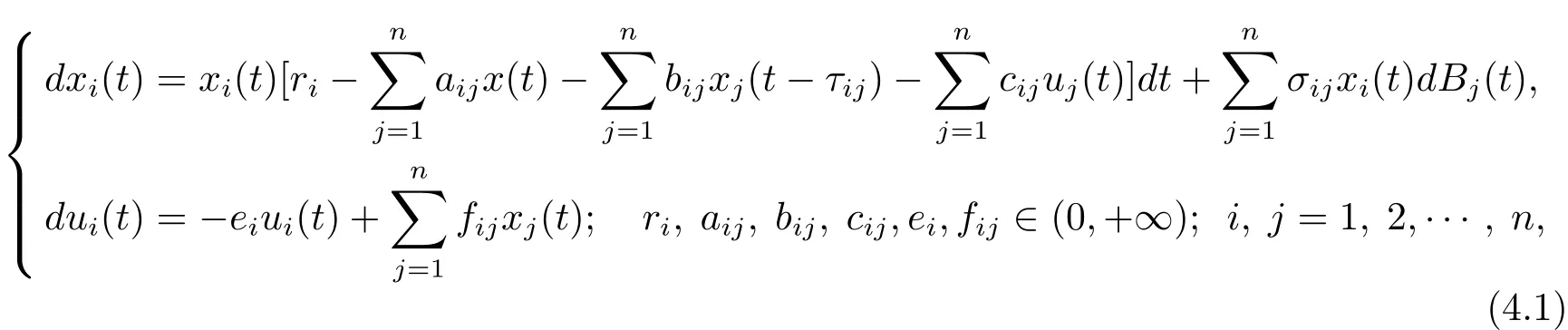
其中xi(t)代表第i個種群的種群密度;ui(t)表示反饋控制變量;τij≥0代表時滯,i,j=1,2,···,n.令初始條件
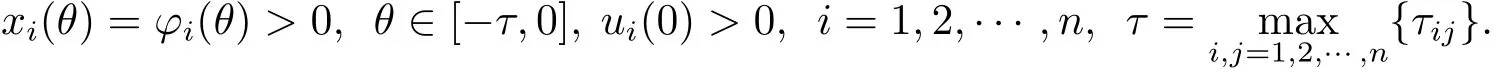
為了方便起見,假設非空集合I={1,2,···,n},Im={l1,l2,···,lm}且集合J滿足
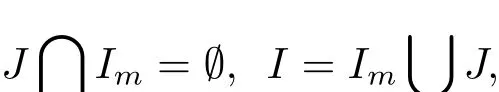
其中 l1 設 Aki表示行列式A第k行第i列的余子式,Bki表示行列式B第k行第i列的余子式. 定理4.1對任意給定的正初始值,系統(4.1)存在唯一全局正解(t≥?τ).如果Ri≠0,則系統(4.1)的解有 定理4.2如果Ri>0且A>0,那么Mi<0,i=1,2,···,n不能同時成立. 證 假設結論不成立,那么Mi<0,i=1,2,···,n,容易得出因為hij都是正常數,故那么很容易看出 也就是說A<0,顯然與A>0矛盾.完成證明. 定理 4.3(i)假設Ri>0且A>0,i=1,2,···,n, (a)如果Mi>0,Aii>0和Aki≤0(k≠i,k,i=1,2,···,n),那么種群xi均值穩定.即 (b)假設Mli>0且Mk<0,li∈Im,k∈J,如果B>0,Gi>0,Bii>0和Bki≤0(k≠i,k,i=1,2,···,n),那么種群xli均值穩定,種群xk將趨于滅絕.即 (ii)如果Ri<0,那么種群xi將趨于滅絕.即 (iii)假設Rli>0且Rk<0,li∈Im,k∈J,如果B>0,Gi>0,Bii>0和Bki≤0(k≠i,k,i=1,2,···,n),那么種群xli均值穩定,種群xk將趨于滅絕.即 證 對于(4.1)式應用伊藤公式,有 結合(4.2),(4.4)和(4.5)式可得 根據定理3.1的證明和定理4.1可知?ε>0,存在T>0,當t≥T,有 把上面不等式代入(4.6)式可得 (i)(a)如果 Ri>0,A>0,Aii>0,Mi>0,i=1,2,···,n.由 (4.7),(4.8) 式和引理3.1,有 (i)(b)如果Rk>0,Akk>0,Mk<0,k∈J.令ε足夠小,使得Mk+ε<0,由(4.7)式和引理3.1,有xk(t)=0 a.s.k ∈ J.,那么 由上面的方法可知 如果B>0,Bii>0,Gi>0,i=1,2,···,m,由(4.10),(4.11)式和引理3.1,有Gi/B a.s.i=1,2,···,m. (ii) 如果 Ri<0,i=1,2,···,n,那么 (iii)如果Rk<0,k∈J,根據(i)(b)的證明易得 在這里就省略了. 本文首先探討了一類具有反饋控制的隨機logistic種群模型,當r?0.5σ2>0時,種群x均值穩定,當r?0.5σ2<0時,種群x滅絕.顯然反饋沒有影響該種群的均值持久性與滅絕性.接著我們在此基礎上把他推廣到n個種群上,構建了一類具有時滯和反饋控制的n個種群的隨機Lotka-Volerra競爭系統,并獲得了該系統中的每一個種群的均值穩定和滅絕的充分條件.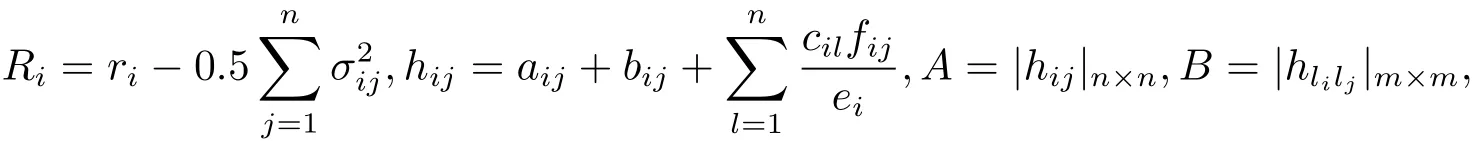
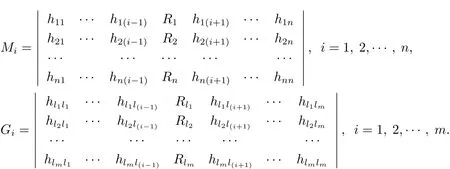
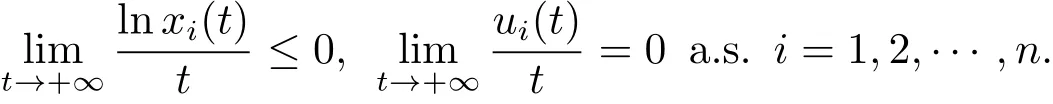
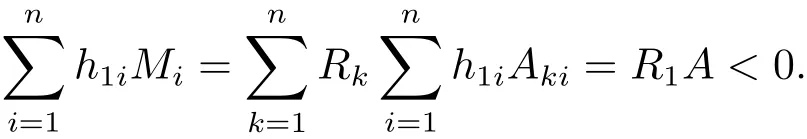
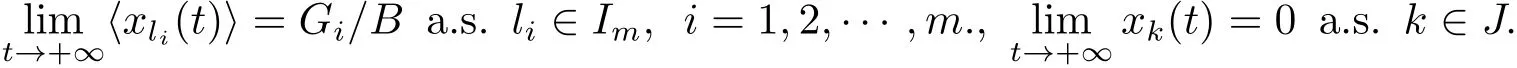
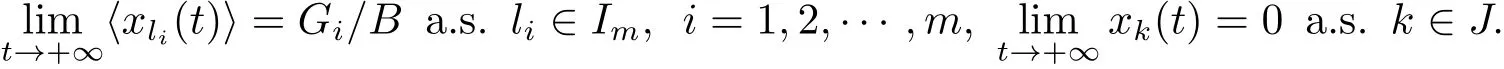
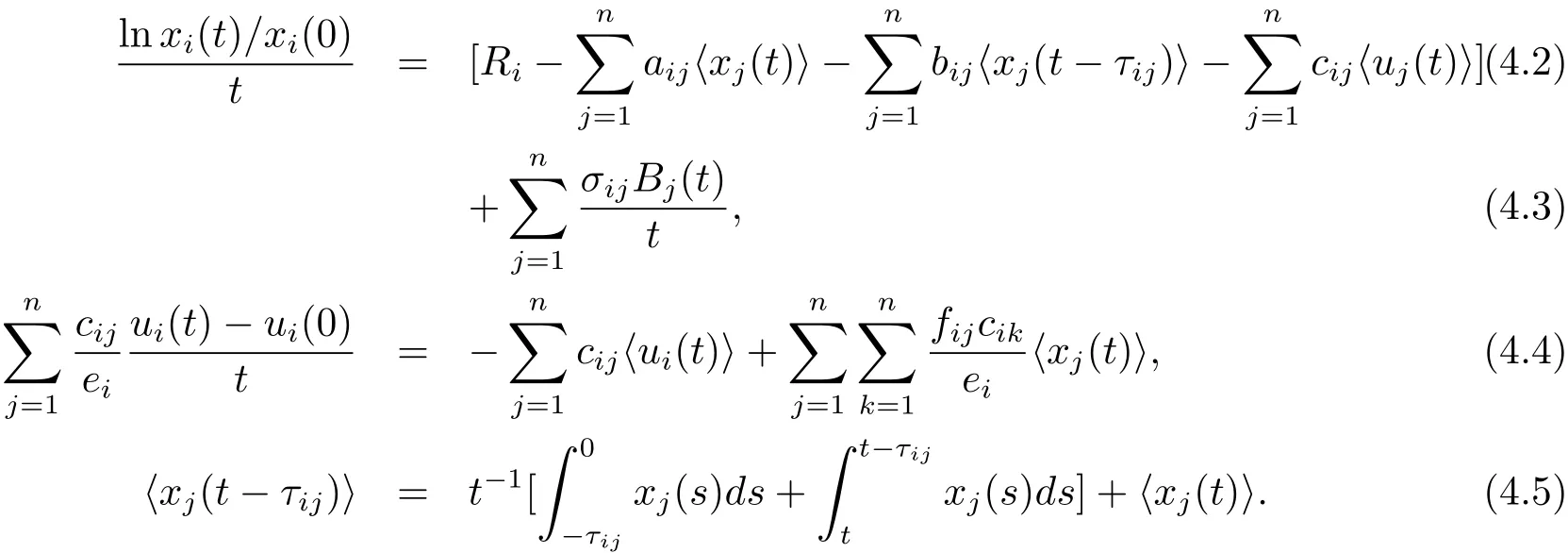
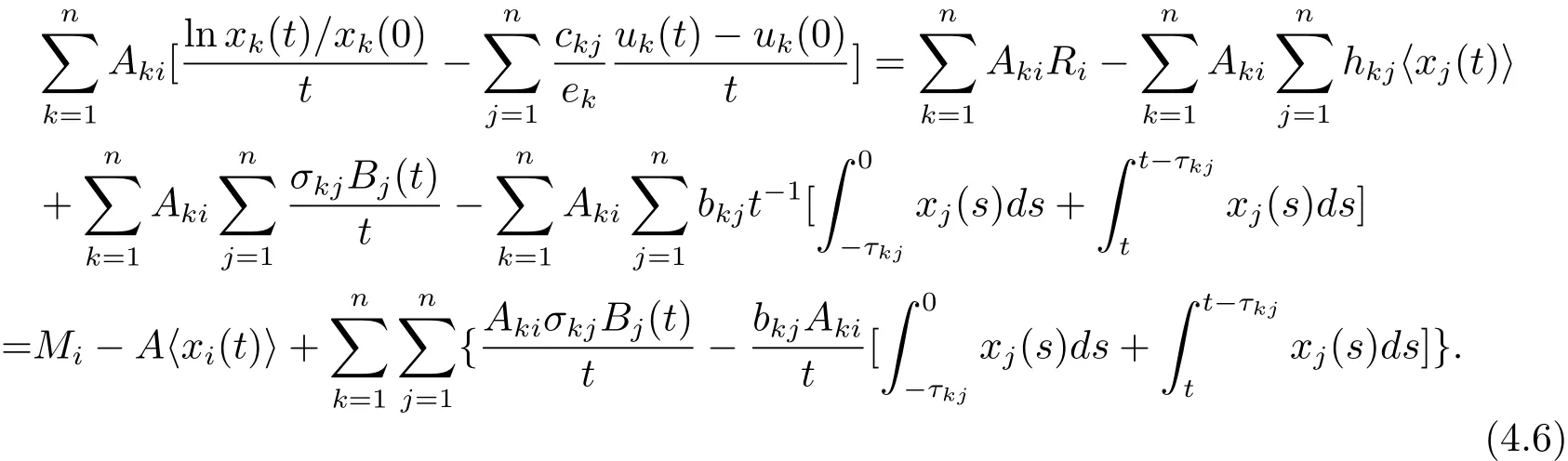
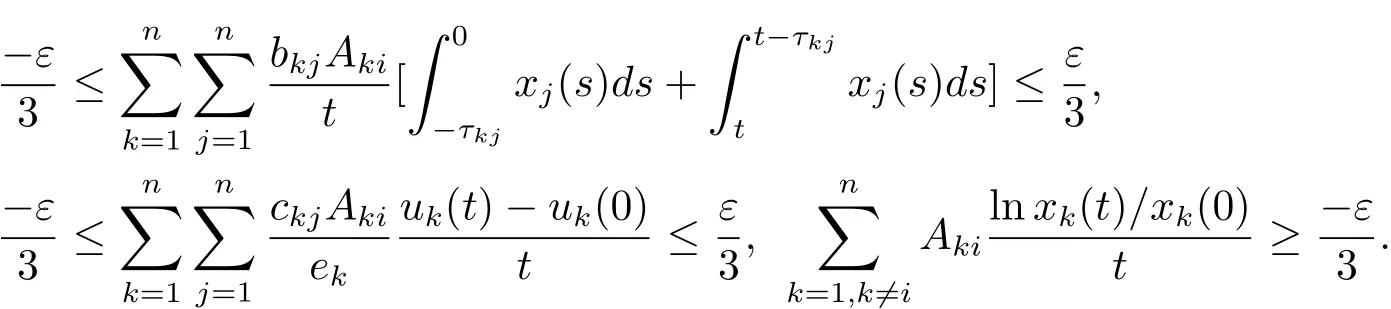
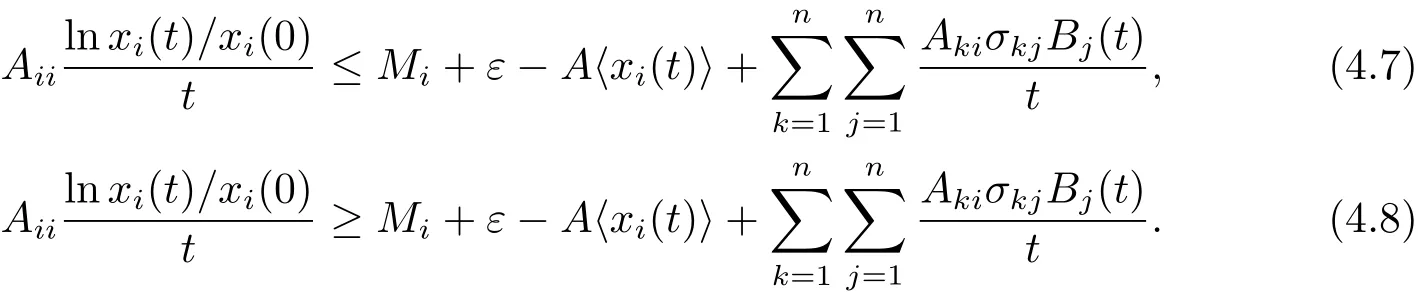
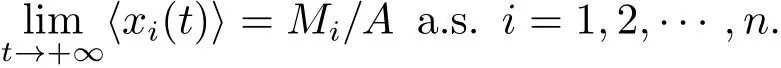
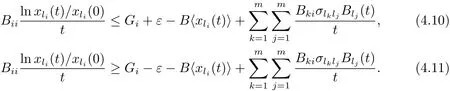
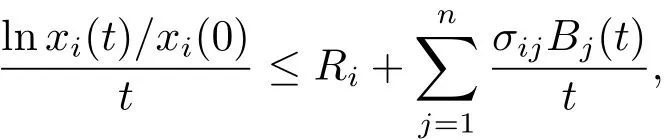
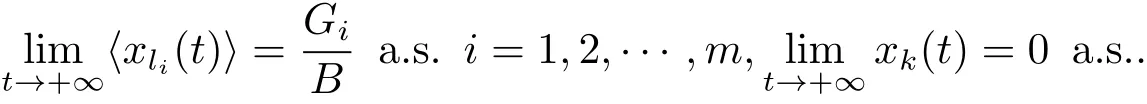
5 結論

