一組帶擾積分算子M-P逆的抗擾投影逼近

高潔

(武漢大學數學與統計學院,湖北武漢 430072)

1 引言

考慮第一類算子方程

其中T∈B(X,Y),f∈Y是已知項,φ∈X 為未知項,這里B(X,Y)表示Hilbert空間X 和Y之間的全體有界線性算子所組成的Banach空間,并以D(T),R(T),N(T)分別表示T的定義域,值域,零空間.

方程(1.1)不一定有解,即使有解也不一定是唯一的.因此,考慮方程(1.1)的最佳逼近解φ∞=T?f,其中T?是T的Moore-Penrose廣義逆.人們感興趣的是dimX=∞時φ∞的有限維投影逼近問題.為此,取完備(正交)投影格式(X,{Xn};Y,{Yn}),即,{Xn}和{Yn}分別是X和Y上的有限維子空間序列,滿足

其中Pn:X→Xn,Qn:Y→Yn為正交投影算子,而IX和IY分別表示X上和Y上的恒等算子.考慮方程(1.1)的有限維投影近似系統

其中Tn:=QnTPn:Xn→Yn,fn=Qnf.我們感興趣的是φn:=能否逼近φ∞:=T?f的問題,文獻[1–8]系統的研究了上述問題,給出了T?的投影逼近格式{}強收斂和弱收斂的充要條件.

對于方程(1.1),還會不可避免的出現擾動問題

其中S∈B(X,Y)適合

文獻[9–20]對擾動問題(1.3)已經作出了系統分析,給出了穩定擾動的一系列刻畫.

本文關心的是T?的投影逼近格式{}的強收斂性是否經得起穩定擾動.即若S適合(1.4)式,是否有

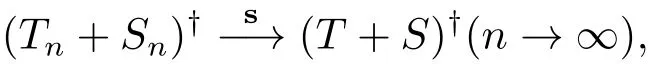
其中Sn:=QnSPn.這是方程(1.1)的計算格式{}及其擾動系統(1.3)的計算格式{(Tn+Sn)?}所面臨的格式擾動基本問題.文獻[21–27]對上述問題在T是單射的情況下給出了一些零散的結果,這些結果有些只能適用于T的定義空間X是有限維的情形[26],鑒于上述問題在一般情形下是一個非常困難的問題,難以給出統一的判斷條件,本文考慮一個特定的積分算子

研究(1.5)引出的第一類算子方程和第二類算子方程的計算格式所面臨的格式擾動基本問題,給出了完整的收斂性分析.

本文以下由三節組成:第二節研究由積分算子(1.5)引出的第一類算子方程;第三節研究了由積分算子(1.5)引出的第二類算子方程;最后一節是結論和評注.

2 第一類算子方程

考慮由積分算子(1.5)引出的第一類算子方程

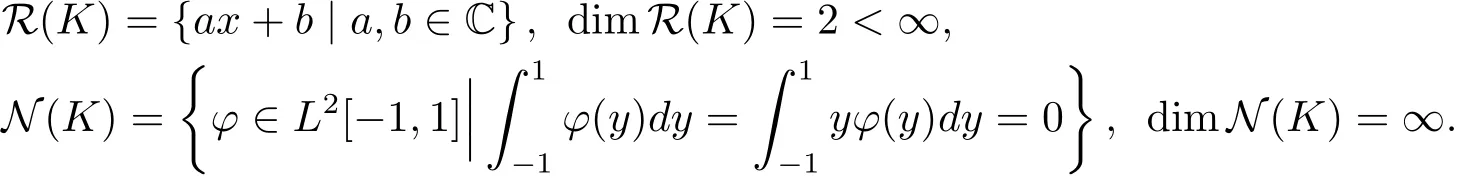
還易知對任意的f=ax+b∈R(T),方程(2.1)有如下最佳逼近解

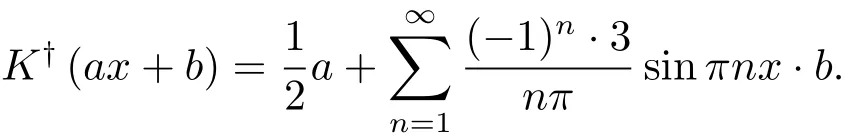
取Xn為

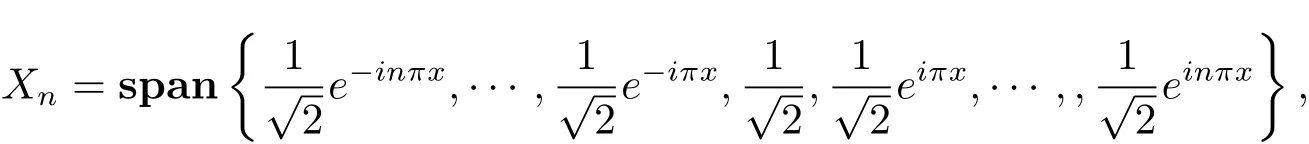
對任意的f∈Y,此時方程(2.1)在Xn上的最佳逼近解為

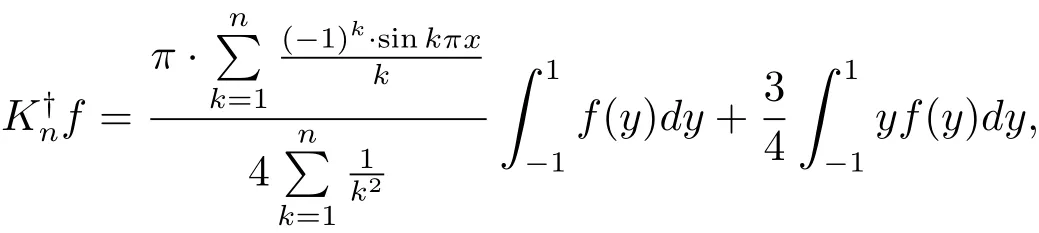
其中Kn:=KPXn.當方程有擾動S∈B(X)時,若S適合條件(1.4),有如下定理.

定理2.1 對上述積分方程(2.1),考慮形如(1.2)的投影方程,其中Xn如上所述,Kn=KPXn,那么進一步,若S適合條件(1.4),則

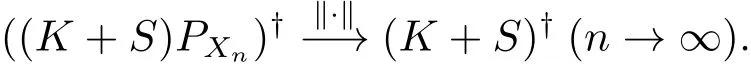
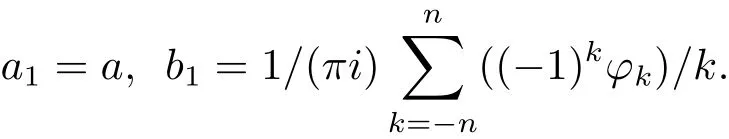
再由f=ax+b,那么

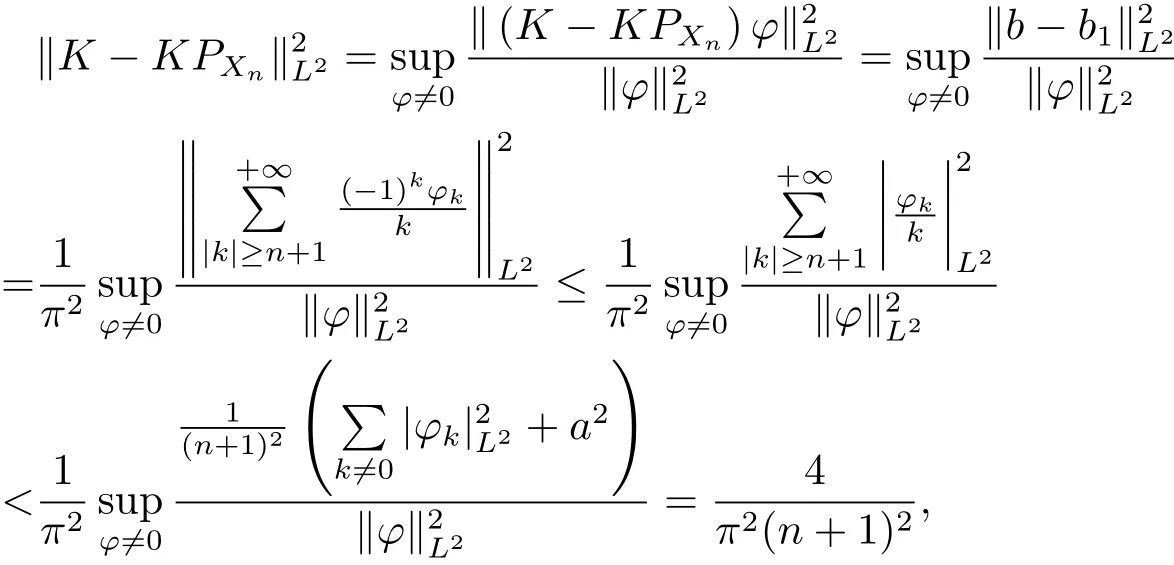
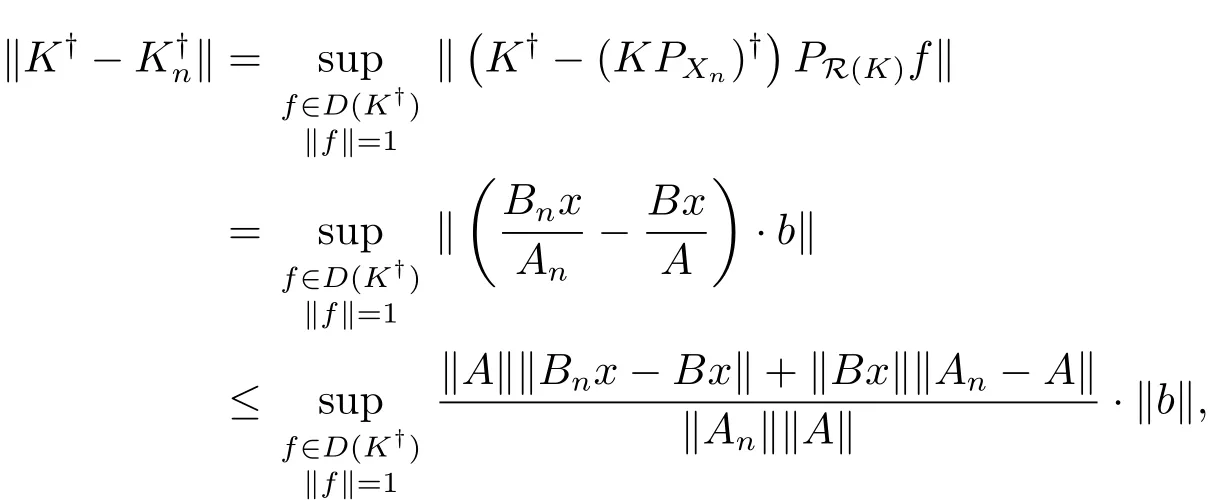
下面考慮有擾動的算子的抗擾穩定性問題,即對任意的S∈B(X),滿足條件(1.5).令eK=K+S,由文獻[18]定理4可知∥?P∥<1,其中,P分別是Y到R(K)及R(K)上的正交投影.再根據文獻[28]可知dimR()=dimR(K)=2<∞,即,K都是有限秩算子,那么S=?K 也是有限秩算子,即dimR(S)<+∞,再利用文獻[29]引理4.2.1,那么則

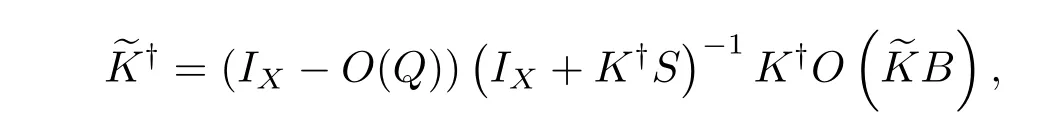
其中 Q=(IX+K?S)?1(IX?K?K),B=(IX+K?S)?1K?,這里 O(Q),O(eKB)表示從X 到R(Q)和從X 到R(eKB)的正交投影,即

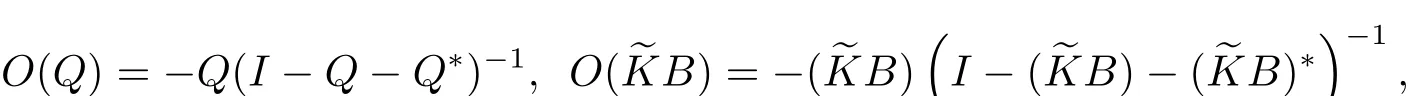
那么

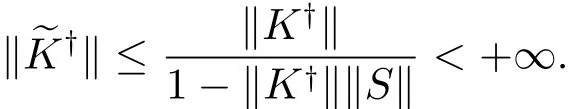
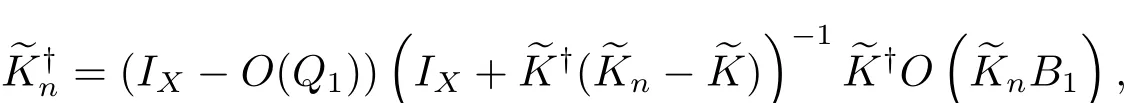
其中

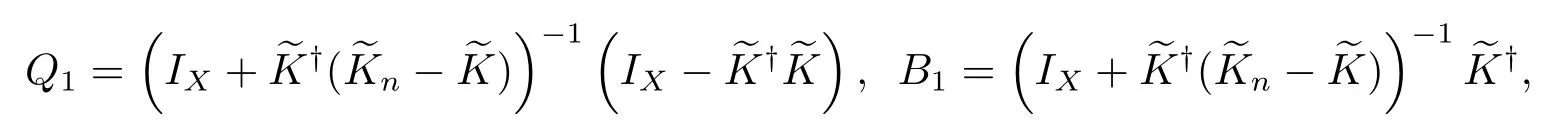
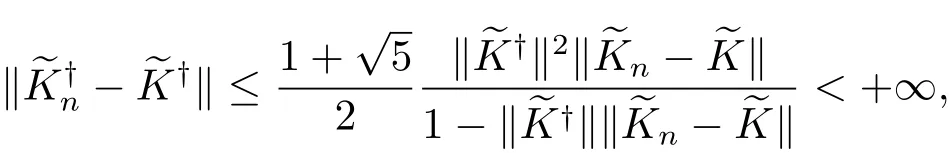
3 第二類算子方程

對λ∈C{0},考慮第二類算子方程

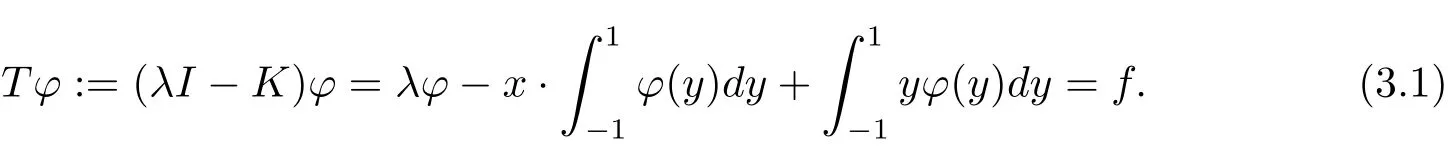
易知

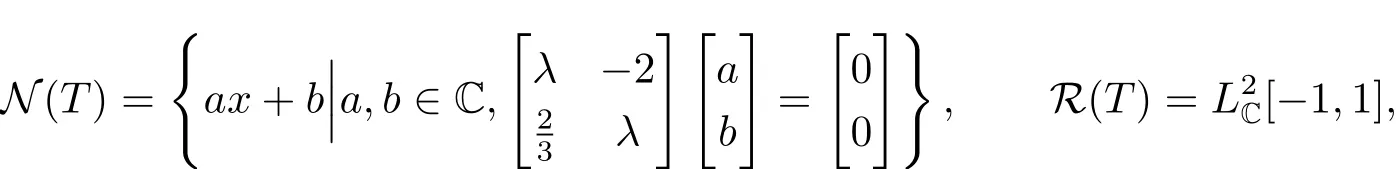
且

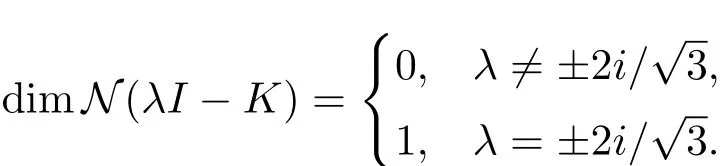
并令Tn:=TPXn,n∈N,其中{Xn}是X的一列適當的有限維子空間.

注3.1 注意,算子T為雙射時,此時子空間的選取如下

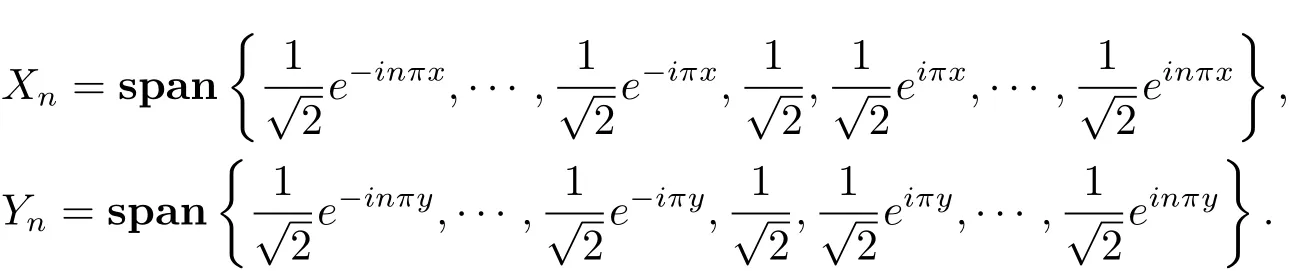
對任意的f∈Y,方程(3.1)的解為

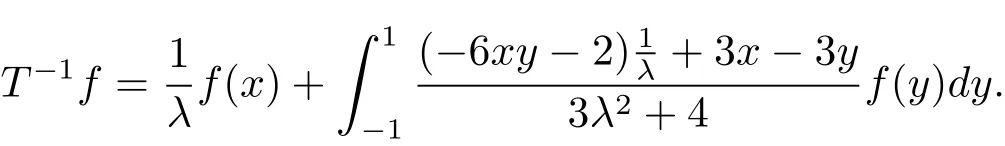
相應的投影解為

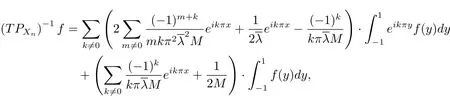
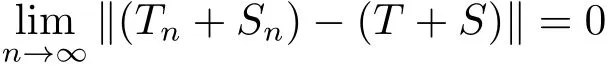
將不會恒成立,即條件(1.4)將無法再保證,而Banach逆算子定理和Neumann級數僅適用于單射的情形.為了研究問題,必須討論穩定性條件

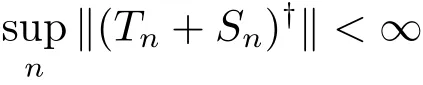
是否成立,根據文獻[4]定理1.1,這只需判斷,是否存在n∈N,使得條件N(T+S)?Xn成立.一般地,上述條件成立有賴于{Xn}的選取.在此我們給出{Xn}的一種選法使上式不成立,從而說明此時方程(3.1)的收斂的投影近似格式經不起穩定擾動.

取Xn,Yn為

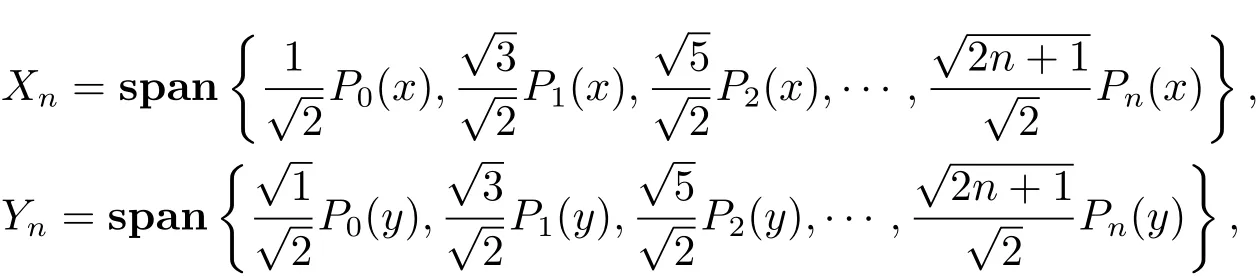
其中

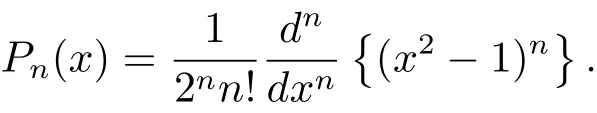
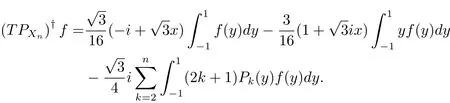
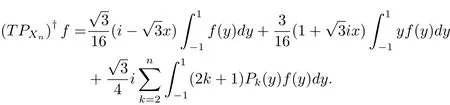
進一步,對任意的S∈B(X),若條件(1.4)成立,如下定理成立.

定理3.1 對上述積分方程(3.1),考慮形如(1.2)的投影方程,其中Xn,Yn如上所述,那么對任意的f∈Y,有

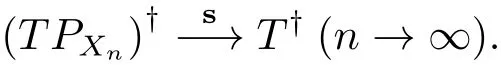
從而積分方程(3.1)的最佳逼近解如下:對任意的f∈Y,

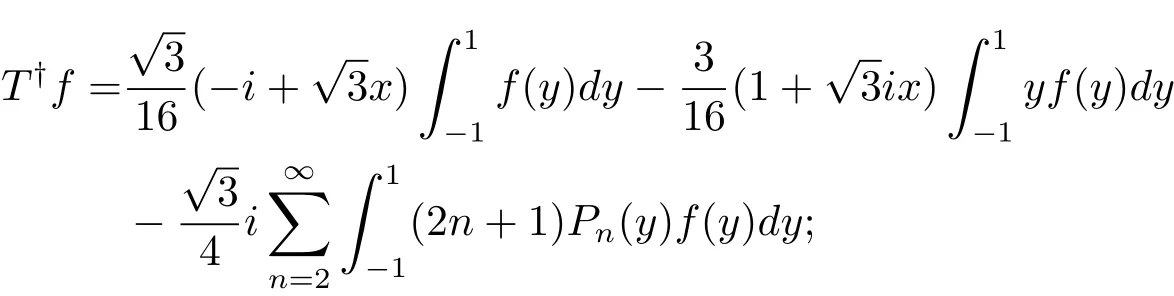
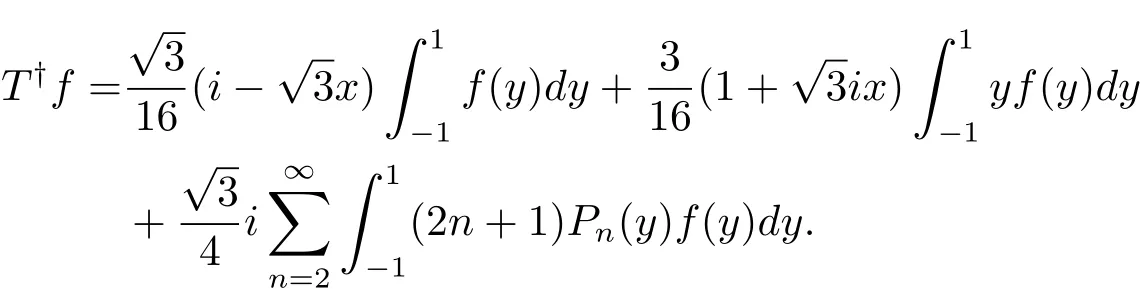
證 由于N(T)?X1,利用文獻[4]定理1.1可知

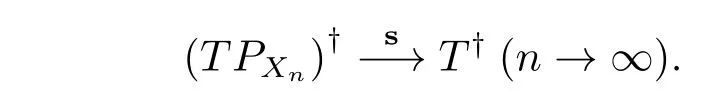
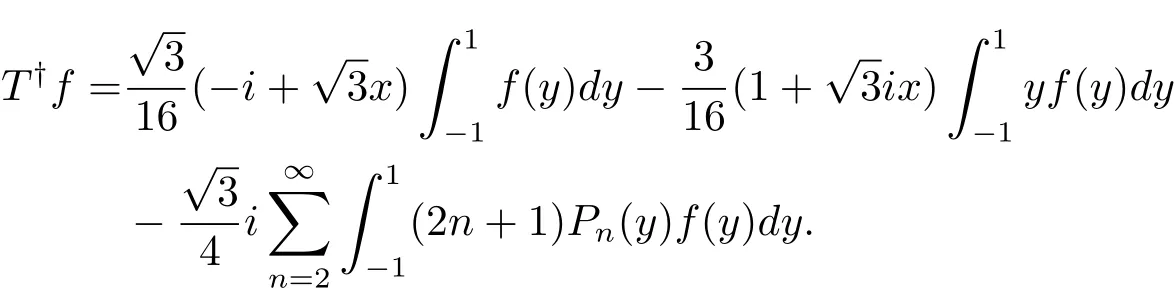
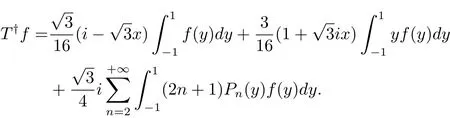
下面考慮擾動的情況,當S∈B(X),下面給出反例,說明在不補充其他條件的情況下,經不起穩定擾動,請看下面的反例.

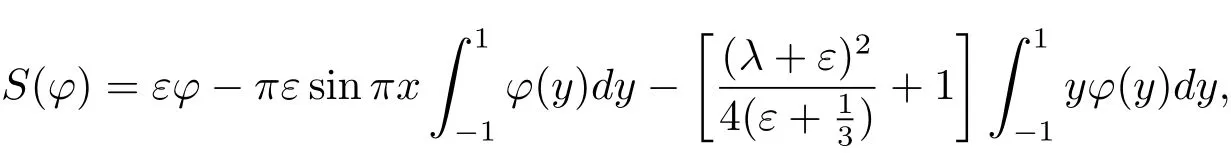
那么S∈B(X,Y),且對充分小的ε,滿足條件(1.4),那么

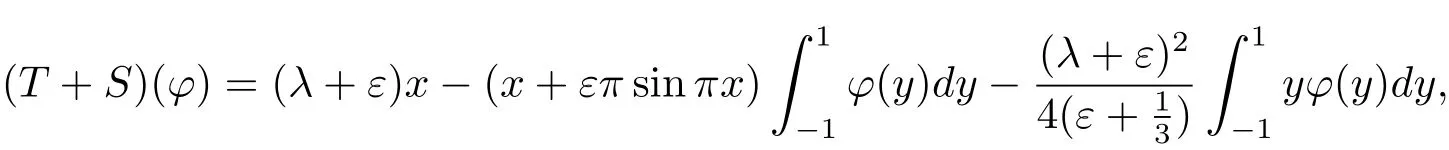
由于

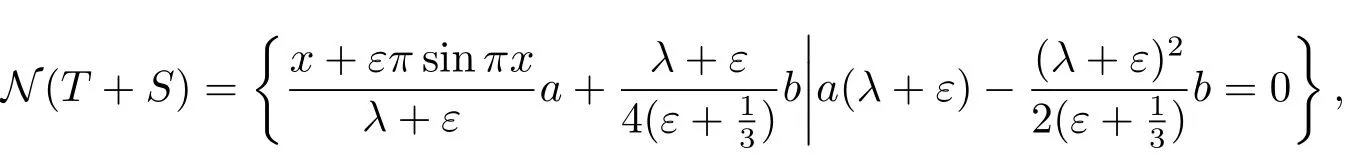
且dimN(T+S)=1,但此時不存在n∈N,使得N(T+S)?Xn,由文獻[4]定理1.1可知穩定性條件不滿足,即

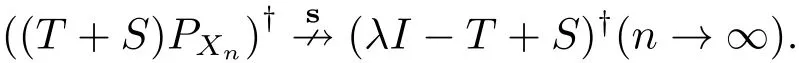
4 總結

對方程(1.5)引出的第一類算子方程(2.1),我們得到了定理(2.1).實際上,對于一般的有限秩算子,定理(2.1)的結論也是成立的,我們有如下的結論.

結論4.1 對積分方程(1.1),設dimR(T)<∞,考慮形如(1.2)式的投影方程,其中{Xn}是X 的一列有限維子空間,Tn:=TPXn,且{Xn}滿足

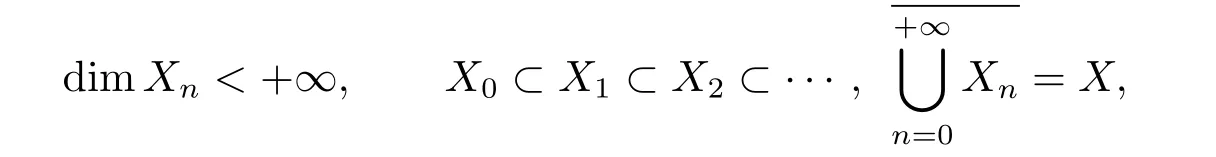
(X,{Xn})為完備(正交)投影格式.那么對任意的f∈Y,有進一步,若S適合條件(1.4),那么

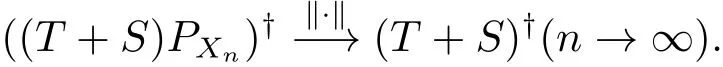
注4.1 上述結論4.1,僅僅只能適用于有限秩算子,但是對于一般的無限維算子,這個結論是不能成立的.

實際上,這兩種情況就是討論了第二類積分方程中λ的選取問題,情況一實際上討論了λ=0,情況二中討論λ是否為算子K 的特征值的情況,這說明針對于算子(1.5),第二類積分方程的最佳逼近解的投影逼近格式是否經得起穩定擾動,與λ的選取有關.因此可以給出如下的推論.

結論4.2 已知積分算子(1.5),設第二類積分方程

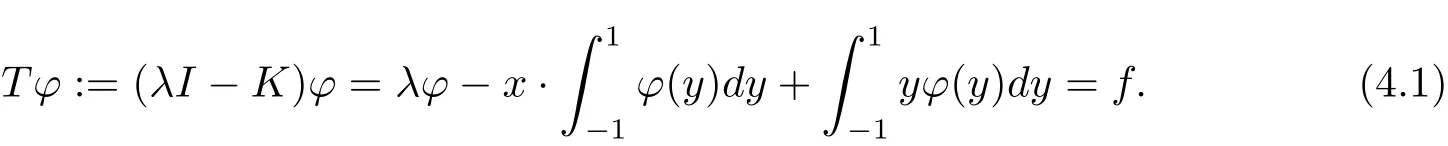
考慮形如(1.2)式的投影方程,其中{Xn}是X 的一列有限維子空間,Tn:=TPXn,且{Xn}滿足

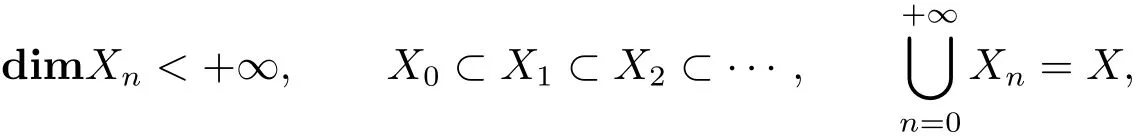
(X,{Xn})為完備(正交)投影格式,對任意的n∈N,滿足穩定性條件:令:=T+S∈B(X,Y),其中S∈B(X,Y)是任意充分小的擾動算子,適合條件(1.4),那么有如下結論