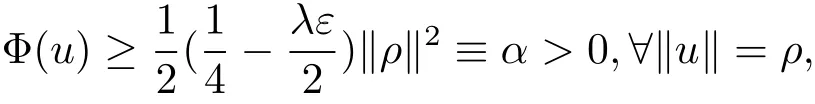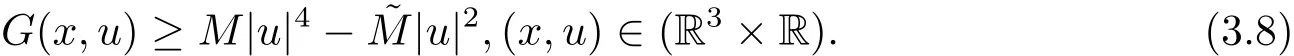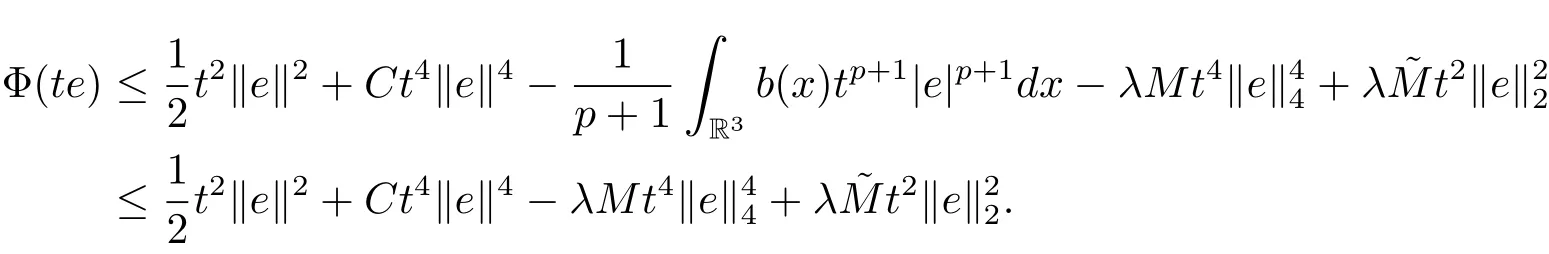一類非線性Schr?dinger-Maxwell方程基態解的存在性
汪敏慶,黃文念,方立婉
(廣西師范大學數學與統計學院,廣西桂林 541006)
1 引言及主要結果
考慮以下非線性Schr?dinger-Maxwell方程基態解的存在性.
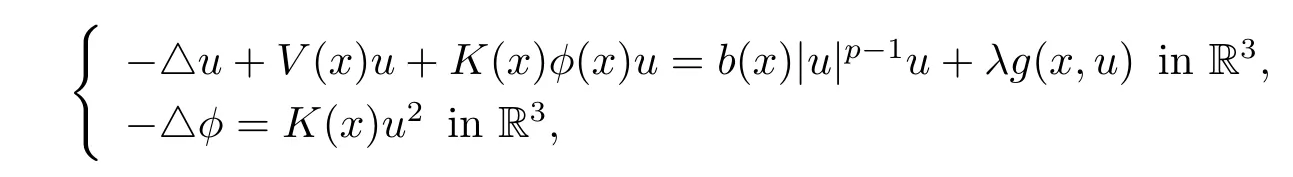
這樣的方程又被稱為Schr?dinger-Poisson方程.在量子力學中,該方程可描述帶電粒子與電磁場的相互作用(關于物理方面的更多的描述可詳見文獻[1]).
過去的幾十年里,在臨界點理論和變分法的幫助下,類似于系統(1.1)的系統的解的存在性、不存在性和多重性得到了廣泛的研究,具體可參考文獻[2–4].進一步地,當V(x)≡K(x)≡1,f(x,u)=|u|p?1u,1 對V,K,b,g有以下假設 (V)V(x)∈C1(R3,R),V(x)≥ a1>0,其中a1>0是一個常數.對每一個M>0,meas{x∈R3,V(x)≤M}<∞. (K)K ∈L∞(R3,R),對任意的x∈R3,有K(x)≥0. (B)b:R3→R+是一個正連續函數,并且,其中 0 (g1)g(x,u)∈C(R3×R,R),g在xi(i=1,2,3)中是1-周期的,且|g(x,u)|≤C(1+|u|q?1),其中 2 (g2)當u→0時,對所有的x∈R3,有g(x,u)=o(u). (g3)當u→∞時,對所有的x∈R3,有 (g4)對任意的(x,u)∈(R3,R),有其中G(x,u) 對于系統(1),主要的結果如下 定理 1.1 假設(V),(K),(B),(g1)–(g4)成立,則系統(1.1)存在一個基態解,其中C>0表示一系列不同的正常數. 定義下列函數空間H1(R3)={u∈L2(R3)|?u∈(L2(R3)3}.對應的范數為 定義函數空間D1,2(R3):={u∈L2?(R3):?u∈(L2(R3)3}.對應范數為 令 則E是一個Hilbert空間,對應的內積為 記∥·∥為Ls(R3)下的范數,H=為H(R3)空間中徑向函數的子空間,則H 可以緊嵌入Ls(R3),其中s∈(2,6)[16].再記 則E是連續嵌入到Ls(R3)中的,s∈[2,2?],這里的2?=6是在三維空間里Sobolev嵌入的臨界指數.因此,存在一個常數C>0,使得 其中 是在Lebesgue空間Ls(R3)下的范數. 因為K ∈L∞(R3,R),故對每一個u∈E,由H?lder不等式,有 由Lax-Milgram 定理(詳見文獻[11])可知,對任意的u∈E,存在唯一的?u∈D1,2(R3),使得 對于?u,可以寫成下列積分形式 故由x∈R3,K(x)≥0可知,?u(x)≥0.結合(2.1)和(2.2)式,有 因此由H?lder不等式和(2.1)式,有 定義泛函I:E→R 從上面的討論可知I是C1的,并且I的臨界點就是問題(1.1)的解.進一步地,由(2.3)式有 如果u∈E 是泛函Φ的一個臨界點(也就是Φ′(u)=0),則(u,?u)是系統(1.1)的一個解.進一步地,對任意的u,v∈E,有 特別地, 定義對應的 Nehari流形為 N={u ∈ E:?Φ′(u),u?=0}.設 (X,∥·∥)為 Hilbert空間,{ej}為其一組標準正交基,令 定義2.1設E是一個實Banach空間,Φ∈C1(E,R),c∈R.當n→∞,un∈E時,如果對任意滿足 的序列{un}?X都有收斂的子列,則稱Φ滿足(PS)c條件. 為了證明定理1.1,我們將會利用以下形式的山路定理(詳見文獻[12,13,14]). 定理2.2[12,13,14]設E是一個實Banach空間,Φ∈C1(E,R),Φ(0)=0,對任意的c>0,Φ滿足滿足(PS)c條件,且 (i) 存在 ρ,α >0,使得 Φ|?Bρ≥ α; (ii)存在e∈EBρ,使得Φ(e)≤0.則Φ有一個臨界值c≥α. 引理2.3[15]對任意的2≤s<2?,有 引理3.1 若(V),(K),(B),(g1)–(g4)成立,e∈E{0},則 (i) 存在 ρ,α >0,使得 Φ|?Bρ≥ α. (ii)當|t|→∞,Φ(te)=?∞. 證 (i)由假設(g1),(g2)可知,對任意的ε>0,存在C(ε)>0,使得對所有的x∈R3,u∈R,有 因此,由中值定理,有 由引理2.3及p∈(0,1)可知,存在Re>0,使得當∥u∥≥Re時,有 于是,對于u ∈ Zk,∥u∥≥ Re,有 您可通過以下三種方式關注《臨床神經病學雜志》微信公眾平臺:1、搜索公眾訂閱號名稱“臨床神經病學雜志”添加關注;2、搜索微信號“lcsjbx”添加關注;3、掃描位于本刊目次頁右上角的微信二維碼。 (ii)由(g3)可知,對任意的M>0,存在ξ=ξ(M)>0,使得對所有的x∈R3,|u|>ξ,有 由(g1),(g2)可知,存在M1=M1(M)>0,使得對所有的x∈R3,0<|u|≤ξ,有 由(3.6)式和中值定理可知,對所有的x∈R3,|u|≤ξ,有 引理3.2若(V),(K),(B),(g1)–(g4)成立,則Φ滿足(PS)c條件. 證 設序列{un}?E
主站蜘蛛池模板:
国产免费网址|
乱人伦中文视频在线观看免费|
九九香蕉视频|
欧美日韩va|
最新亚洲人成无码网站欣赏网
|
夜夜爽免费视频|
美女无遮挡免费网站|
日韩成人在线网站|
欧美yw精品日本国产精品|
亚洲v日韩v欧美在线观看|
亚洲最大福利网站|
无码中文字幕乱码免费2|
国产99视频免费精品是看6|
国产麻豆精品手机在线观看|
久久99精品久久久大学生|
国产精品亚洲а∨天堂免下载|
又爽又大又黄a级毛片在线视频|
青青草国产精品久久久久|
91av成人日本不卡三区|
久久黄色视频影|
中文无码日韩精品|
欧美亚洲一区二区三区导航|
国产成人一区在线播放|
国产精品页|
毛片视频网址|
美女啪啪无遮挡|
91无码人妻精品一区二区蜜桃|
黄色片中文字幕|
毛片网站在线看|
黄色在线不卡|
亚洲人成影院在线观看|
免费大黄网站在线观看|
欧美亚洲第一页|
亚洲天堂在线免费|
青草娱乐极品免费视频|
久久伊人操|
精品一区二区三区波多野结衣|
国产午夜精品一区二区三区软件|
夜夜拍夜夜爽|
九色在线观看视频|
日本成人不卡视频|
久久久久久尹人网香蕉
|
在线观看免费AV网|
国产青榴视频|
成人年鲁鲁在线观看视频|
狠狠操夜夜爽|
国产jizzjizz视频|
99这里只有精品6|
欧美翘臀一区二区三区|
欧美成人精品在线|
亚洲一区二区日韩欧美gif|
亚洲av无码人妻|
欧洲日本亚洲中文字幕|
天天色天天综合网|
成年免费在线观看|
欧美曰批视频免费播放免费|
91视频首页|
国产一级妓女av网站|
免费观看无遮挡www的小视频|
东京热av无码电影一区二区|
国产区福利小视频在线观看尤物|
国模视频一区二区|
国产精品国产三级国产专业不|
国产成人综合在线视频|
91色在线视频|
国产aaaaa一级毛片|
激情乱人伦|
激情综合网址|
日本欧美午夜|
亚洲国模精品一区|
五月天综合婷婷|
国产精品网曝门免费视频|
久久久久国产一级毛片高清板|
婷婷午夜影院|
亚洲欧美在线精品一区二区|
成人午夜网址|
成人在线观看一区|
99久久国产精品无码|
亚洲天堂网视频|
成人一级黄色毛片|
国产精品女人呻吟在线观看|
av色爱 天堂网|
2 預備知識及相關引理
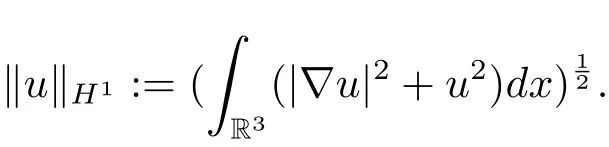
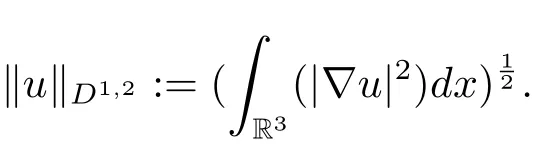
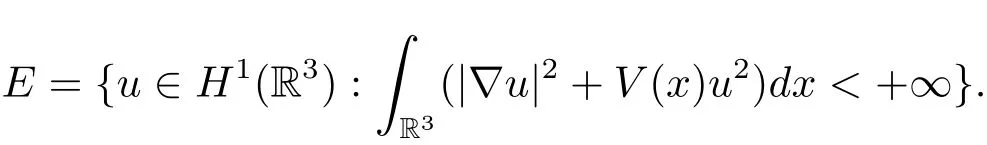
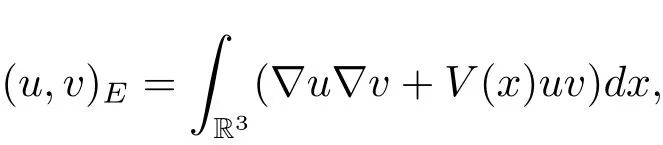
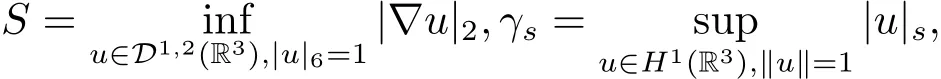

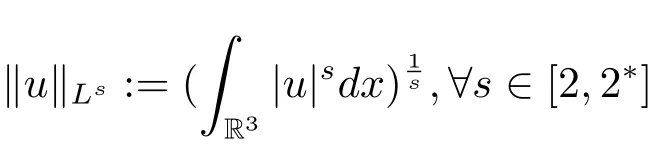
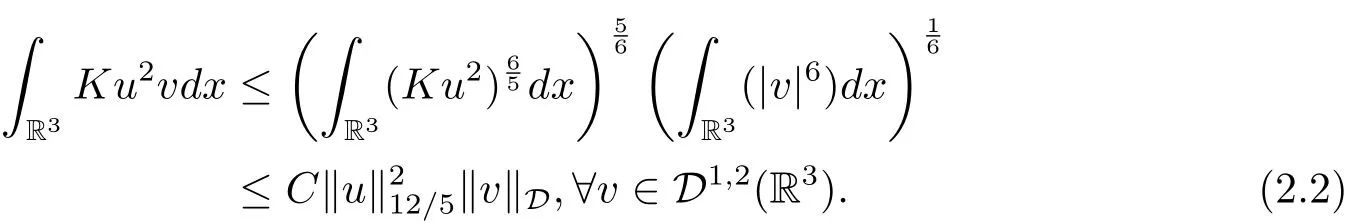

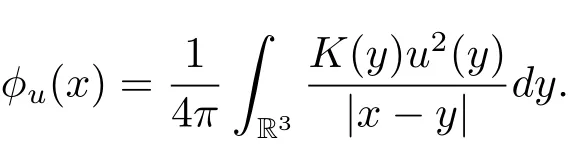
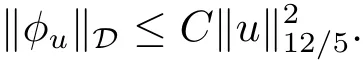

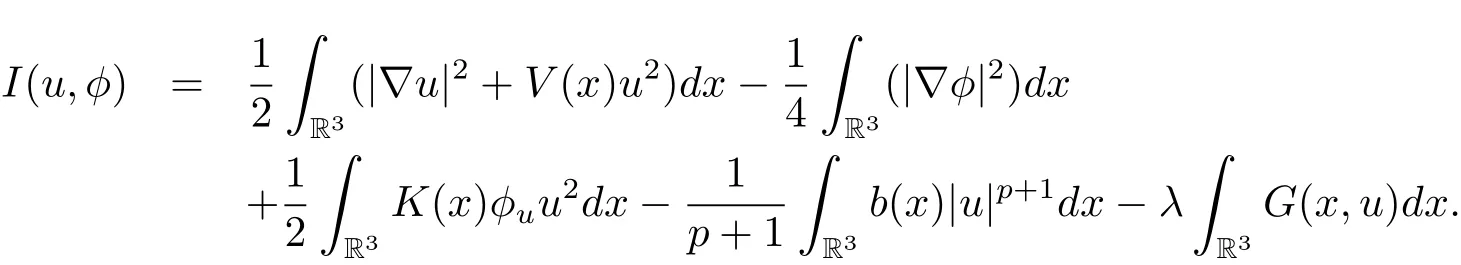
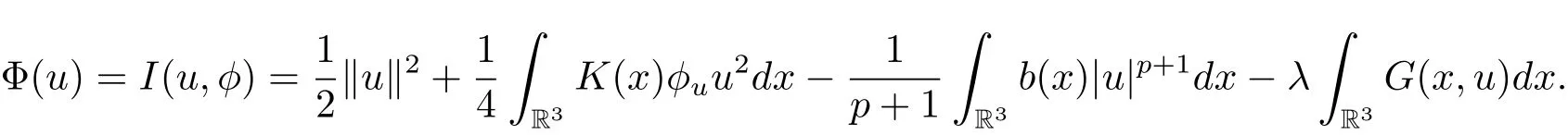
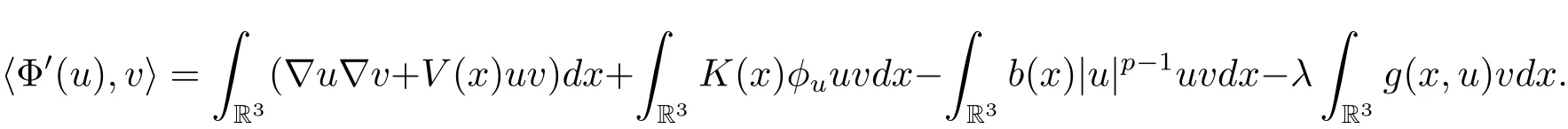
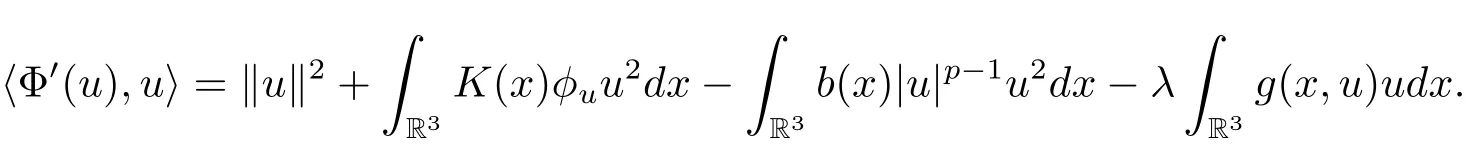
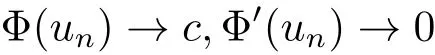
3 定理1.1的證明