面板數據下序貫模型變點的漸近檢驗法

陳卓恒,胡亦鈞

(1.華僑大學數學科學學院,福建泉州 362021)

(2.武漢大學數學與統計學院,湖北武漢 430072)

1 引言

變點問題起源于工業質量控制的領域,在質量控制中非常重要的一點是如何快速檢測出生產線上不合格產品比例的增加.在建模和數據挖掘中,一個很常見的問題是,如何根據現有的樣本數據,來判斷我們感興趣的一些量是否發生變化.這種問題在統計中我們稱其為變點問題.關于變點問題的建模和分析始于Page 1954年發表在《Biometrika》上的文獻[1],文獻主要考慮了利用分位數構造的簡單檢測方法去檢驗生產線上觀察到數據的穩定性.在此之后,關于變點問題的研究變得日益活躍,各種研究文獻也日益增多.而且隨著學科的發展和深入,變點問題在經濟、金融學、生物醫學、氣候學、導航系統、圖像處理、信號探測、計算機等很多領域都有廣泛的應用背景.

很久以來大多數的變點檢測的文獻都是基于這樣的背景:對于一組固定容量的歷史數據集,我們設計一些檢驗方法來判斷這組數據內我們感興趣的參數是否發生變化.這種檢驗即為我們常說的“事后檢驗”.在這種檢驗中,樣本是靜態的,這種數據我們稱為是離線數據.離線數據分析主要在譬如歷史文本分析,圖像分析等領域有應用.但是在更多的領域譬如質量控制,醫療監測,金融風險控制,我們使用的都是在線數據,也就是樣本采取連續抽樣的方式得到的.采取連續抽樣的方式來得到樣本進行檢驗,這種檢驗稱為“序貫檢驗”.序貫檢驗也是最近幾年變點檢測中的研究熱點.具體來說,在序貫檢驗中,一般假定靜止期的長度為m,也就是在m個觀察數據X1,X2,···,Xm內不存在變點,這m個觀察數據也常稱為歷史數據.在考慮漸近性質的時候一般令m→∞.在原假設成立即認為沒有變點存在的情況下Xm+1,Xm+2,···的參數是相同的;若備則假設成立即認為變點存在的情況下,則存在一個整數 k?≥ 0,使得 Xm+1,Xm+2,···,Xm+k? 的參數與歷史數據相同,而 Xm+k?+1,Xm+k?+2,···的參數不同,這里k?為未知變點.接下來要做的就是如何構造合適的檢驗統計量并制定合理的停止規則,從而判斷變點是否存在以及在認為變點存在的情況下推斷出變點的位置,使得變點從產生到被檢測出需要的時間盡量的短,并盡量消除誤報,即快速準確檢測出變點.

文獻[2]是較早提出并研究變點檢測中序貫檢驗的代表性文獻之一,文中提出了兩種檢測方案,一種利用波動差,一種利用殘差的累積和,并拓寬了經典的不變原理得到所需要的收斂結果,最后確定了臨界值和停止規則,找到最優停時,并在模擬中得到了檢驗.文獻[3]進一步推廣了文獻[2]的結果,同樣對于線性回歸模型,文獻[3]提出了兩類檢驗統計量,第一類統計量是建立在回歸系數β取最小二乘估計時殘差的加權累積和,第二類是利用回歸系數構造的迭代殘差的部分和得到的統計量.并制定了合適的檢驗規則,使得在歷史數據個數m→∞時錯誤預報率在約定的水平內,且檢驗功效趨于1.學者Aue在變點的序貫檢驗中也做了一系列工作,譬如率先開展研究停止時刻τn的極限分布,得到了文獻[4],后續工作有文獻[5–7],另外文獻[8]得到了在對ARMA時間序列中結構變點進行序貫檢驗時,停止時刻的極限分布.在近幾年中,也有把自助抽樣技術引入到序貫模型中的變點檢測問題中,可參考文獻[9,10]和[11].

目前來說,現有的文獻主要研究單序列情形下的序貫模型,那么,如何在面板數據下研究序貫模型的變點,這是一個嶄新的問題.在本文中,我們主要對這個問題進行研究.本文剩余部分的結構是這樣的:第2節將描述模型并得到相關的理論結果,即檢驗統計量的大樣本性質;第3節基于前面的理論結果提出面板數據下關于變點的漸近檢驗法,并進行了Monte-Carlo模擬計算;第4節給出了前面引理和定理的證明過程;第5節對前面的結論進行了總結.

2 模型及相關理論結果

考慮面板均值變點模型

這里 μij和 εij分別表示均值和面板擾動項.{μij,j=1,2,···,m+Tm}i和 {εij,j=1,2,···,m+Tm}i是相互獨立的.Tm與m 有關而且假定Tm≤ ∞,序列{εij}關于i相互獨立,εij～ (0,σ2)且在概率空間(?,F,P)上關于j是獨立同分布的(i.i.d.).假定0<σ2<∞而且對于某個υ>2有E|εij|υ<∞.

假定對于每個1≤i≤N,已經觀察到長度為m的歷史數據,它沒有變點發生,即對于1≤i≤N,

現在我們感興趣的是接下來到來的數據里是否存在均值發生變化的共同變點,即想檢驗原假設

和備則假設

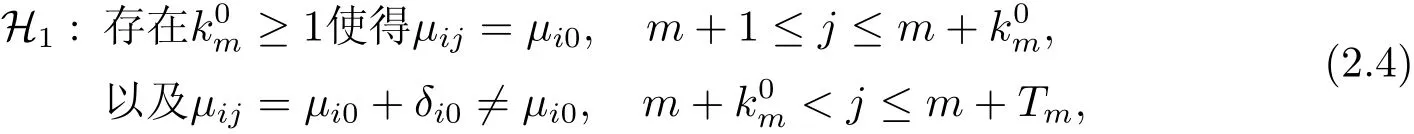
這里σ2,μi0,δi0,k0m的值均為未知.檢測變點的方案是基于CUSUM型檢測統計量Γ(m,k,N)和一個邊界值,這里

此處

此外,基于歷史數據集 {Yi1,Yi2,···,Yim}i=1,2,···,N使用以下的方差估計

關于檢驗法則,在

處停止并拒絕H0.τN(m)也被稱為停時,而且這里的c應該被選擇成使我們能夠控制錯誤預報率.即在原假設H0下,對于某個給定水平0<α<1,

在備則假設H1下,要求

定理2.1對于面板數據模型(2.1),在原假設(i.e.(2.3)式)的假定下,當m,N→∞時,有

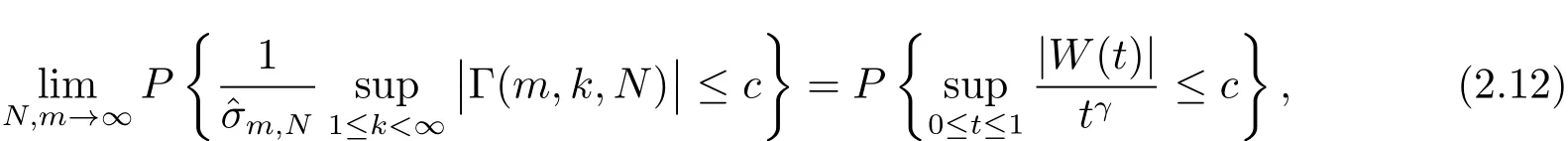
這里{W(t),0≤t<∞}是一個Wiener過程,γ見(2.6)式.

3 漸近檢驗法及其模擬計算

根據定理2.1知,在原假設成立即沒有變點時,若m,N→∞時,

的極限分布為

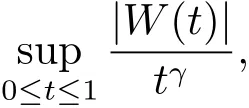
這里{W(t),0≤t<∞}是一個Wiener過程.因此可以通過此處已知的極限分布求出在給定的顯著性水平下檢驗的臨界值c,然后利用這里的臨界值c以及檢驗法則來確定是拒絕還是接受原假設,并在原假設被拒絕,即認為變點存在的情形下估計出變點的位置.這種方法我們稱它為“漸近檢驗法”.

關于漸近檢驗法,首先要計算檢驗的臨界值.由于臨界值只與γ有關,所以可記作cγ.為了計算經驗檢驗水平,考慮一個不帶變點的模型,并且計算

的次數,這樣就得到了這個次數和Monte-Carlo模擬次數之比.進一步,為了計算經驗檢驗功效,考慮帶一個變點的模型,并進行M 次Monte-Carlo模擬.在這M 次模擬中,計算出檢驗統計量

超過臨界值cγ的頻率,然后來計算經驗檢驗功效.同時,|Γ(m,k,N)|超過臨界值cγ的最早出現的那個k被認為是變點位置的估計值.

一般來說,作為一個好的檢驗方法,經驗檢驗水平應該小于或等于給定的水平,而且經驗檢驗功效應該足夠大.另外,在變點后的停時應該足夠的短才好.因此首先按照定理2.1來計算臨界值cγ.

第二步 在這M 次模擬的基礎上,計算臨界值cγ,使得P[Uγ>cγ]=α.

表1:由50000次Monte-Carlo模擬計算出的臨界值cγ

接下來,在表2–8中,利用表1中計算出的臨界值cγ,分別計算了在γ,Tm,N,m 取不同值,變點k0m在不同位置(左端,中間或右端)時,漸近方法的經驗檢驗水平,檢驗功效以及停止時刻的各數字特征.具體來說:

表2:利用cγ經1000次Monte-Carlo模擬計算出的經驗檢驗水平,N=200,Tm=500

表3:利用cγ經1000次Monte-Carlo模擬計算出的經驗檢驗水平,Tm=500,m=100

表4:利用cγ經1000次Monte-Carlo模擬計算出的檢驗功效,N=200,Tm=500,k0m=25

表5:利用cγ經1000次Monte-Carlo模擬計算出的檢驗功效,N=200,Tm=500,m=100

從表2可以看出,當m固定時,隨著γ的增大,經驗檢驗水平越小.當γ固定時,隨著m的增大,經驗檢驗水平越小.從第一行和第二行的數據可以看到,當γ=0和0.25時,若歷史數據集m較少,得到的經驗檢驗水平是會超過給定水平的.從而可以考慮在[0,1/2)的范圍內選取較大的γ,來降低檢驗犯第一類錯誤的概率.而m越大,即沒有變點的歷史數據越多,得到的經驗檢驗水平越小,這與我們的直觀感覺也是相符合的.

從表3可以看出,γ的大小對經驗檢驗水平影響很大,類似表2的表現.當N 固定時,隨著γ的增大,經驗檢驗水平是降低的.在γ=0時,經驗檢驗水平甚至超過了給定的水平.同時注意到,N的大小對經驗檢驗水平的影響不大,不過比較而言,中等大的N似乎能產生相對較低的經驗檢驗水平.

通過模擬得到的列出的,譬如表4,以及一些未列出的表格發現,當變點發生在m個經驗數據之后不久時,則無論m和N 值如何變化,對于不同的α和γ,檢驗的功效都達到了1.

從表5可以看出,在變點k0m在m之后不久或者是更遠一些,檢驗的功效都是1.但是,在變點靠近右端點時,檢驗的功效會降低,最高不超過0.35.在k0m固定時,隨著γ的增大,功效是越來越低的.因此,基于檢驗水平和檢驗功效的考慮,應該選取不大不小的γ,譬如取γ=0.25,從而使兩者能達到一種平衡.

表6:N=200,Tm=500,=25,模擬次數1000次計算出的停止時刻的各數字特征

表6:N=200,Tm=500,=25,模擬次數1000次計算出的停止時刻的各數字特征

γ m=30 m=100 τm ↓;α → 0.025 0.05 0.10 0.025 0.05 0.10 0 Min 9.00 8.00 6.00 26.0 16.00 13.00 Q1 28.00 27.00 27.00 28.0 28.00 27.00 Median 28.00 28.00 28.00 28.0 28.00 28.00 Mean 28.44 28.06 27.58 28.5 28.22 27.92 Q3 29.00 29.00 29.00 29.0 29.00 29.00 Max 32.00 32.00 31.00 32.0 31.00 31.00 0.25 Min 5.00 4.00 4.00 26.00 26.00 11.00 Q1 28.00 28.00 27.00 28.00 28.00 27.00 Median 28.50 28.00 28.00 29.00 28.00 28.00 Mean 28.51 28.17 27.73 28.53 28.27 27.94 Q3 29.00 29.00 29.00 29.00 29.00 29.00 Max 33.00 32.00 31.00 32.00 31.00 31.00 0.45 Min 26.00 20.00 10.00 27.00 26.00 26.00 Q1 28.00 28.00 28.00 28.00 28.00 28.00 Median 29.00 29.00 29.00 29.00 29.00 29.00 Mean 29.21 28.84 28.5 29.12 28.83 28.55 Q3 30.00 30.00 29.00 30.00 29.00 29.00 Max 33.00 33.00 32.00 32.00 32.00 31.00 0.49 Min 27.00 26.00 19.00 27.00 26.00 26.00 Q1 29.00 28.00 28.00 29.00 28.00 28.00 Median 30.00 29.00 29.00 29.00 29.00 29.00 Mean 29.57 29.17 28.88 29.47 29.12 28.83 Q3 30.00 30.00 30.00 30.00 30.00 29.00 Max 34.00 33.00 33.00 32.00 32.00 32.00

從表6看出,如果以停止時刻τm的中位數和均值作為判斷標準的話,在γ固定時,m值的變化對停止時刻的影響不大,也就是說,對變點的估計值影響不大.但是,在m值固定時,隨著γ的增大,變點估計值與真實值的偏差是越來越大的.

從表7可以看出,在N 固定時,隨著γ的增大,變點值的估計偏差也是越來越大的,不過這些偏差的相差量不會很大,不超過1或者2.若γ固定,當N 從50變到300時,變點估計值的精確度明顯提高了,在真實變點=25時,精確度提高了4～5個值.從這里可以看出,增大面板數據的橫截面個數N,是可以明顯提高變點估計的精確度的.

表7:Tm=500,m=100,=25,模擬次數1000次計算出的停止時刻的各數字特征

表7:Tm=500,m=100,=25,模擬次數1000次計算出的停止時刻的各數字特征

γ N=50 N=300 τm ↓;α → 0.025 0.05 0.10 0.025 0.05 0.10 0 Min 23.00 8.00 8.00 26.00 12.00 10.00 Q1 30.00 30.00 29.00 27.00 27.00 27.00 Median 32.00 31.00 31.00 28.00 28.00 28.00 Mean 31.79 31.13 30.56 27.94 27.66 27.44 Q3 33.00 32.00 32.00 28.00 28.00 28.00 Max 41.00 40.00 39.00 30.00 30.00 30.00 0.25 Min 26.00 23.00 18.00 26.00 26.00 12.00 Q1 31.00 30.00 30.00 27.00 27.00 27.00 Median 32.00 31.00 31.00 28.00 28.00 28.00 Mean 32.08 31.52 30.98 27.99 27.78 27.58 Q3 33.00 33.00 32.00 28.00 28.00 28.00 Max 42.00 41.00 41.00 30.00 30.00 30.00 0.45 Min 27.00 27.00 26.00 26.00 26.00 26.00 Q1 32.00 31.00 30.00 28.00 28.00 27.00 Median 33.00 32.00 32.00 28.00 28.00 28.00 Mean 33.29 32.59 32.01 28.44 28.18 27.98 Q3 35.00 34.00 33.00 29.00 29.00 28.00 Max 45.00 44.00 42.00 31.00 31.00 30.00 0.49 Min 27.00 26.00 26.00 27.00 27.00 26.00 Q1 32.00 32.00 31.00 28.00 28.00 28.00 Median 34.00 33.00 33.00 29.00 28.00 28.00 Mean 34.14 33.30 32.65 28.75 28.45 28.21 Q3 36.00 35.00 34.00 29.00 29.00 29.00 Max 46.00 45.00 43.00 31.00 31.00 31.00

最后看下在N,Tm,m都固定,而變點在不同位置時,變點位置估計值的情況.在表8中,若=25,這種情形在前面已經探討過.我們來看下=390,即變點處于右端點的情形.從表格中的數據可以發現,對于這種變點最好以變點的中位數而不是均值作為變點的估計值,因為中位數會離真實變點接近的多,估計的偏差在5到6之間.同時γ的大小與估計量的精確度的關系類似表7中的表現,在N固定時,γ越大,估計的偏差也會相對大一些.

通過以上表格的具體分析,發現參數γ該如何選取是個很有趣的事情.從表2看出,較小或者中等大的γ(γ=0,0.25)且m取較小或中等大(m=30,100)時,數據表明經驗檢驗水平與給定的水平接近.類似地,在表3中,γ=0,N=100同樣可使得經驗檢驗水平接近給定的真實值α.我們再來看看參數γ與檢驗功效的關系.表4中的檢驗功效對應著變點較早發生的情形,這時,無論γ在區間取何值,對應的檢驗功效均為1.從表5看,在變點靠近右端點時,γ越小(其它參數都固定)時,檢驗功效越大.同樣,對表6–8的模擬結果進行分析可知,越小的γ可使變點的估計值與真實值的偏離程度越小.根據以上這些分析,若從經驗檢驗水平,檢驗功效以及變點估計的精確度三方面來綜合考慮,我們傾向于選取區間中較小的γ,從而達到最佳的檢驗和估計效果.

表8:N=200,Tm=500,m=100,模擬次數1000次計算出的停止時刻的各數字特征

4 定理的證明

在這一節中,將給出所有引理和定理的證明.

引理2.1的證明 注意到

那么

而且

經過計算可得

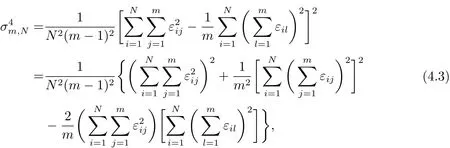
于是有

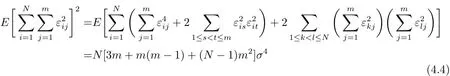
和

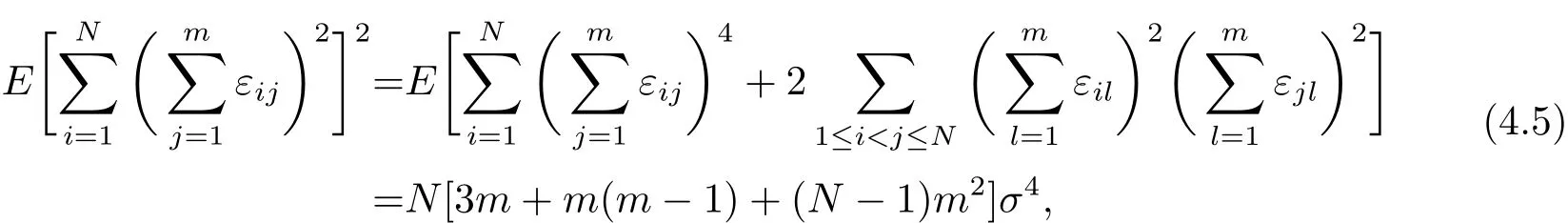
以及

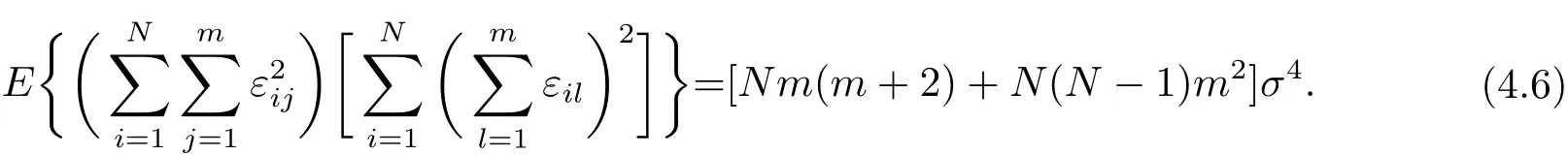
由(4.2)–(4.6)式以及Chebyshev不等式,得到

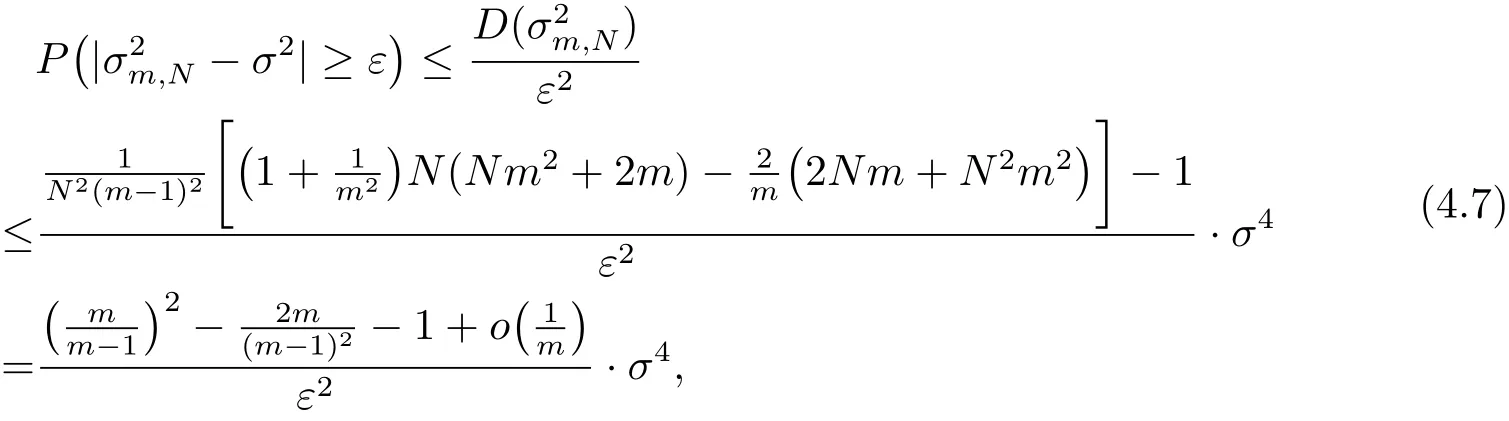
定理2.1的證明 借用文獻[3]中的思想來證明定理2.1.對于面板數據模型(2.1),在原假設(i.e.(2.3)式)下,注意到

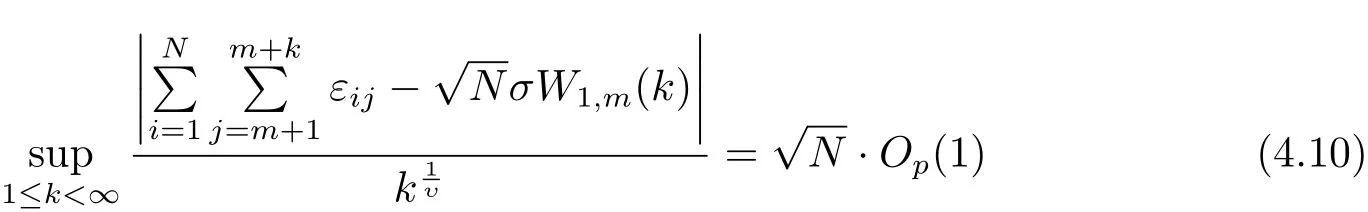
和

此處{W1,m(t)}和{W2,m(t)}是相互獨立的Wiener過程,且v>2.從而推得

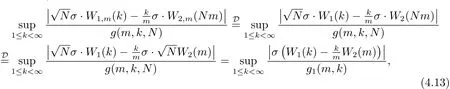
接下來,利用

由文獻[3]中的定理2.1的證明,有

以及

于是定理2.1得到了證明.

由定理2.1以及Chebyshev不等式,得到

5 結論

本文針對面板數據的序貫模型下的可能變點,提出了CUSUM型檢驗統計量并制定了檢驗規則.隨后得到了檢驗統計量的大樣本性質,并基于相關理論結果構造了一種檢驗方法:漸近檢驗法.接下來,對漸近檢驗法進行了Monte-Carlo數值模擬,在模擬中對檢驗方法的經驗檢驗水平,檢驗功效進行了考察,并在變點存在的情況下估計出變點的位置.模擬顯示漸近檢驗法是一種優良的檢驗估計方法.最后給出了理論結果的證明.