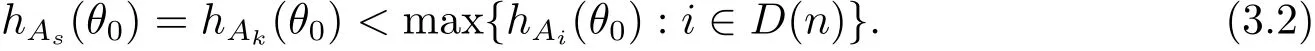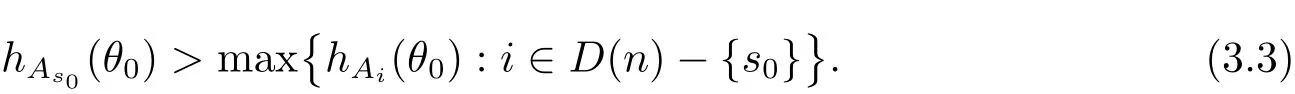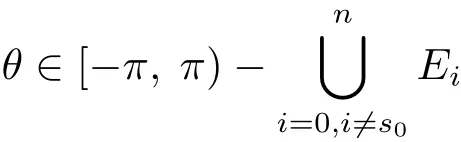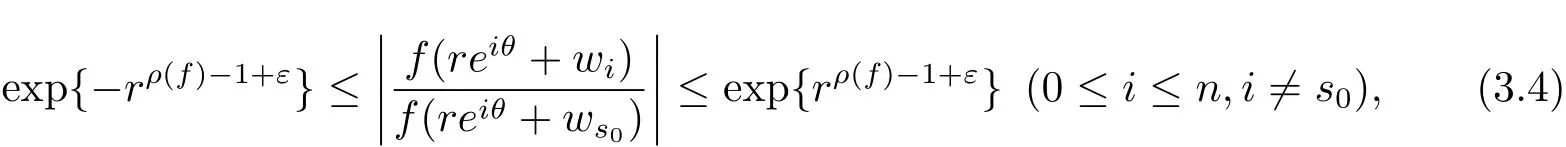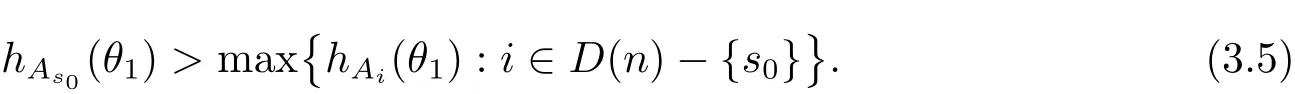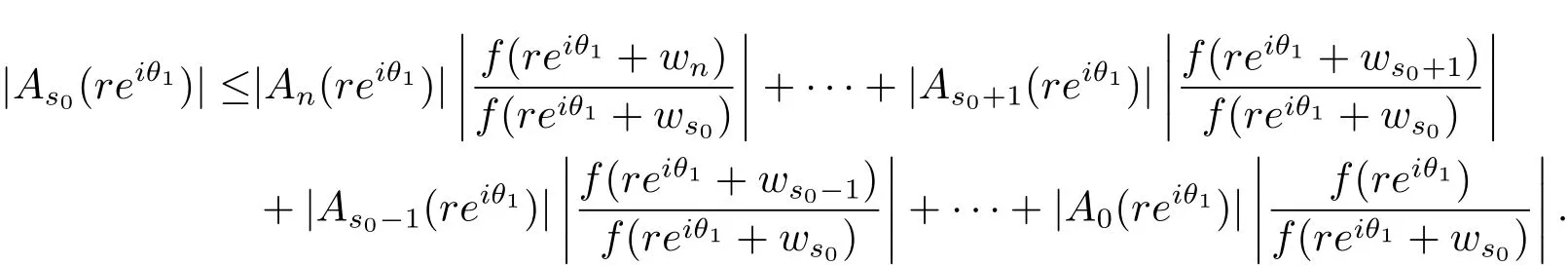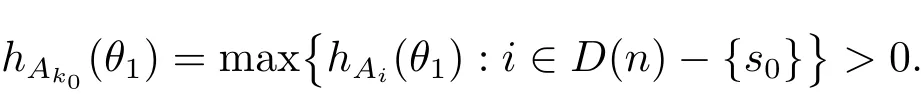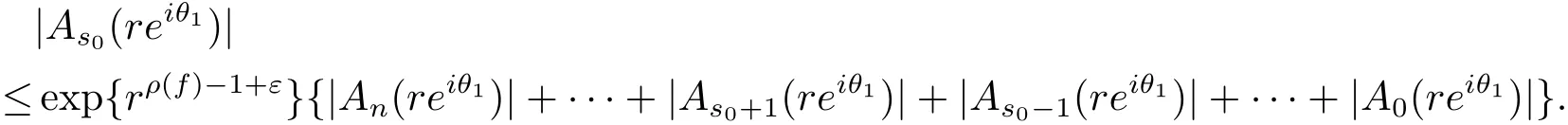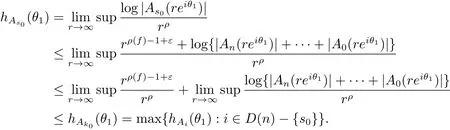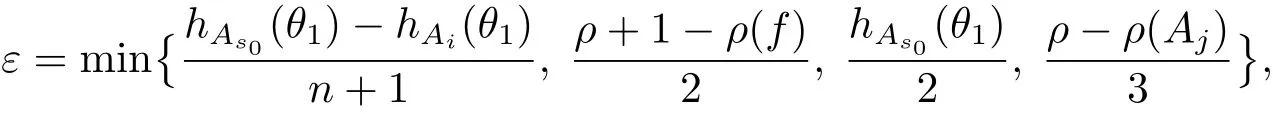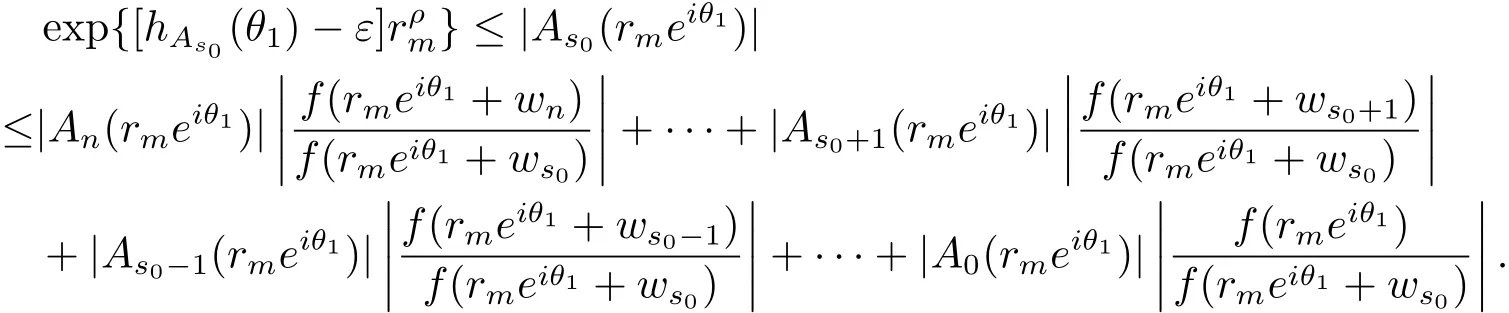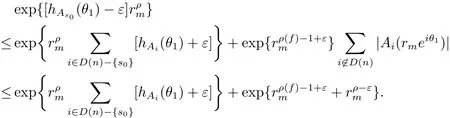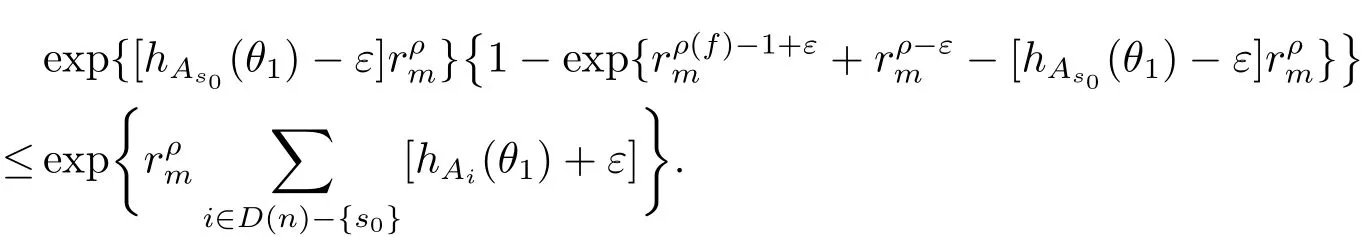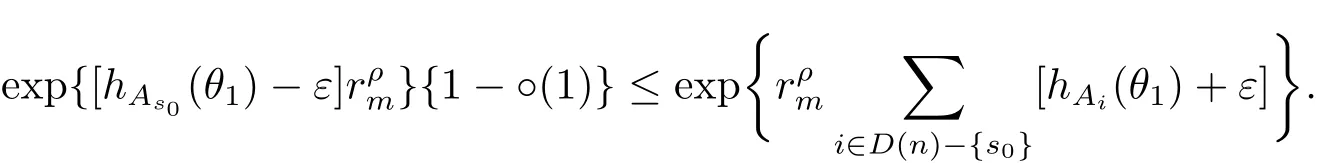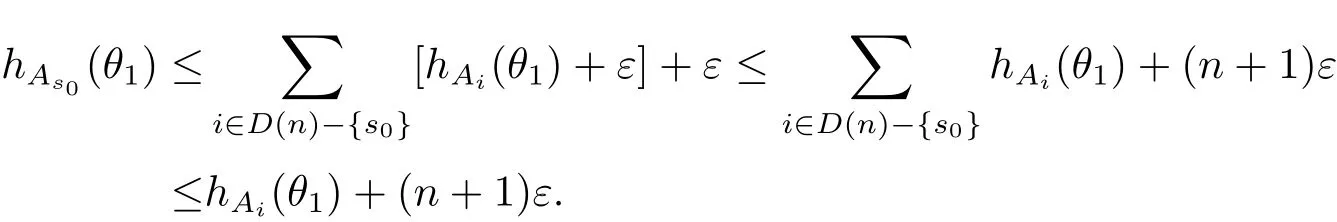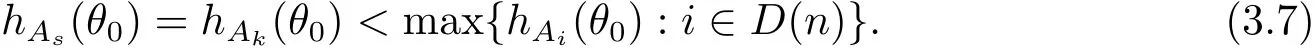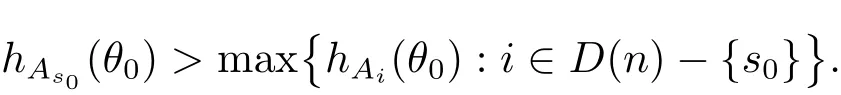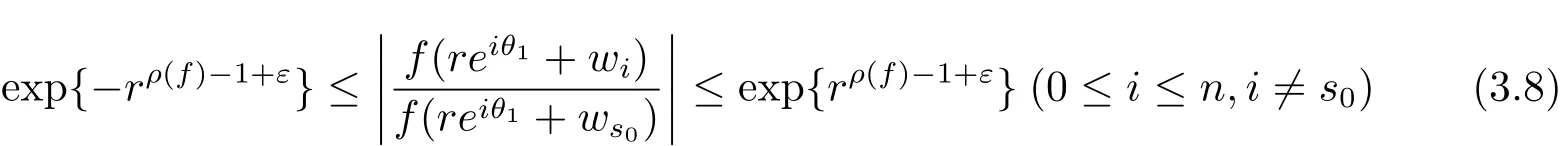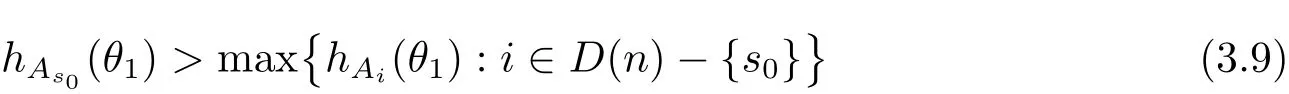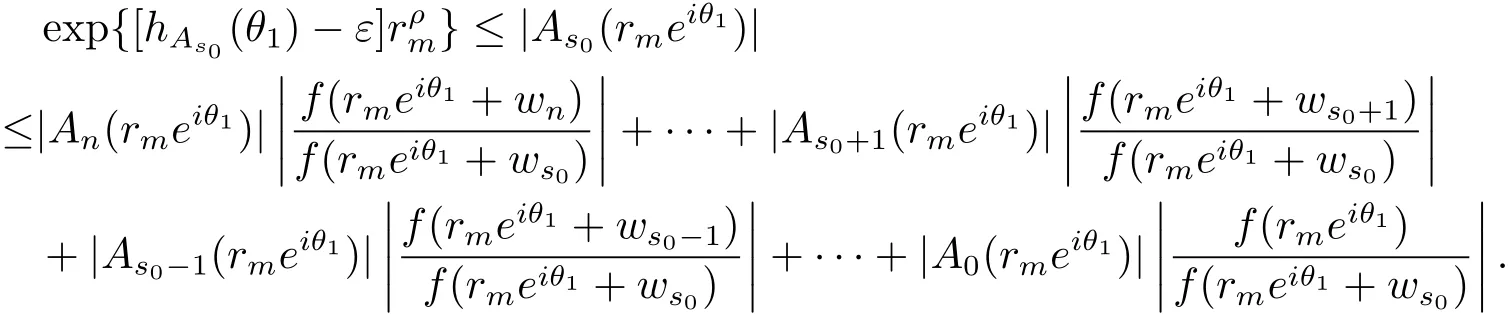關于一類高階性線差分方程亞純解的增長性
吳秀碧,張石梅,龍見仁,2,石 磊
(1.貴州師范大學數學科學學院,貴州貴陽 550001)
(2.北京郵電大學計算機學院;理學院,北京 100876)
1 引言及結果
近年來,有大量的文獻關注復差分方程的亞純解的增長性問題,例如參考文獻[1]和[2]等.本文主要考察以下形式的線性差分方程
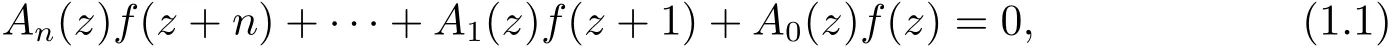
其中Aj(z)(j=0,···,n)均是整函數.
2008年,Chiang和Feng研究了方程(1.1)解的增長性,并給出了其解增長級的一個下界估計.
定理A[3]設Aj(z)(j=0,···,n)均為多項式,且存在l:0≤l≤n使得max{deg(Pj):0≤j≤n,j≠l} 同時,他們還考慮了方程系數為超越整函數的情形,也給出了方程解的增長級的下界估計. 定理B[3]設Aj(z)(j=0,···,n)均為整函數,且存在l:0≤ l≤ n使得max{ρ(Aj):0≤ j≤ n,j≠l}< ρ(Al).如果f(z)是方程(1.1)的任意非零亞純解,則必有ρ(f)≥ρ(Al)+1. 當系數都是多項式時,稱次數等于max{degPj(z):0≤j≤n}的系數為主導系數;當系數有超越整函數時,稱增長級等于max{ρ(Aj(z):0≤j≤n}的系數為主導系數.注意到定理A和定理B的共同點就是都只有一個主導系數.如果方程擁有多個主導系數時,是否還有相應結論?這個問題引起很多研究人員的關注.2011年,陳宗煊考慮了這個問題,在弱化定理A的條件下,得到如下定理. 定理C[2]設系數P0(z),···,Pn(z)均為多項式,且滿足Pn(z)P0(z)0和 如果f(z)是方程(1.2)的任意非零解亞純解,則必有ρ(f)≥1. Laine和Yang改進了定理B,并證明了以下結果. 定理 D[4]假設Aj(z)(j=0,···,n)均為有窮級整函數,wj(j=0,···,n)為任意復常數,且型最大的主導系數僅有一個.記ρ=max{ρ(Aj):0≤j≤n},則方程 的任意非零解都滿足ρ(f)≥ρ+1. 同時,Laine和Yang還提出如下問題. 問題 如果方程型最大的主導系數不止一個,定理B或定理D的結論是否還成立? 2015年,Heittokangas[5]等應用Phragmén-Lindel?f指標函數來研究二階微分線性微分方程解的增長性,得到很多結果.受到文獻[5]的研究方法的啟發,本文利用指標函數研究高階線性差分方程問題,為此先回顧Phragmén-Lindel?f指標函數的定義. 對于一個有窮正級整函數g(z),其指標函數定義為 如果g(z)的型有限,則hg(θ)是一個連續有上界的函數.且對任意ε>0,易知 為了方便敘述起見,我們引入以下符號.對于n+1個有窮正級的整函數Aj(j=0,···,n),ρ =max{ρ(Aj):0 ≤ j ≤ n},記主導函數指標集為 D(n),即 D(n)={j:ρ(Aj)=ρ},并用|D(n)|表示D(n)的元素個數. 本文得到如下幾個結果. 定理1.1 設Aj(z)(j=0,···,n)是有窮正級整函數且至多有一個為無窮型,wj(j=0,···,n)為任意復常數,記ρ=max{ρ(Aj):0≤ j≤ n}.如果方程 有一個非零解f(z)滿足ρ(f)< ρ+1,則對于任意的θ∈[?π,π),要么max{hAi(θ):i∈D(n)}≤0,要么存在s,k∈D(n)使得 如果方程(1.5)的所有系數的增長級都相同時,我們得到下面的結果. 定理1.2 設Aj(z)(j=0,···,n)是有窮正級整函數且至多有一個為無窮型,wj(j=0,···,n)為任意復常數,記ρ=max{ρ(Aj):0≤ j≤n}且|D(n)|=n+1.如果方程(1.5)有一個非零解f(z)滿足ρ(f)<ρ+1,則對于任意的θ∈[?π,π),必存在s,k∈D(n)使得 由以上兩個定理及其證明過程,容易得到以下推論. 推論 1.3 設Aj(z)(j=0,···,n)是有窮正級整函數且至多有一個為無窮型,記ρ=max{ρ(Aj):0≤j≤n},如果存在θ0∈[?π,π)和某個s0∈D(n)滿足下列三個條件之一 那么方程(1.3)的每個非零解f(z)都滿足ρ(f)≥ρ+1. 為了證明上述定理,需要如下的幾個引理. 引理1[3]設η1,η2是任給的兩個復數,f(z)是一個有窮級的亞純函數,則對于任意給定的正數ε,必有相應的性線測度為零的集合E?[0,2π)且當θ?E時,必存在正常數R0=R0(θ)>1,當z滿足argz=θ和|z|≥R0時,有 引理2 設A(z)和B(z)為整函數且滿足下列條件之一 (1)ρ(B)< ρ(A)∈ (0,+∞)且 hA(θ)≥ 0; (2)ρ(B)= ρ(A)∈ (0,+∞)且 hA(θ)>0 ≥ hB(θ); (3)ρ(B)= ρ(A)∈ (0,+∞)且 hA(θ)≥ hB(θ)>0. 則有 同時由hA(θ)的定義可得,對任意ε>0,有 于是結合(2.2)和(2.3)式便有 由于ε的任意性便得結論. 當A(z)和B(z)滿足條件(2)或者條件(3)時,類似(2.3)式有 從而由(2.3)和(2.4)式,并注意到hB(θ)?hA(θ)≤0,于是有 同理由于ε的任意性便得結論. 引理3 設A(z)為有窮正級且型有窮的整函數,f(z)是亞純函數且滿足ρ(f)<ρ(A)+1.則對任意給定η1,η2和充分小的ε>0,必有相應的性線測度為零的集合E?[0,2π)且當θ?E,存在正常數R0=R0(θ)>1,當z滿足argz=θ和|z|=r充分大時,有 同時由hA(θ0)的定義可得有 由(2.5)和(2.6)式便知 注意到ρ(A)>ρ(f)?1+ε,于是當r充分大時就得引理結論. 定理1.1的證明 根據D(n)的定義可知D(n)非空且元素多于一個,否則由定理C便得方程(1.3)的每一個非零解都滿足ρ(f)≥ρ+1.易知對于任意i∈D(n),Ai(z)都為有限型.若不然,假設存在i0∈D(n)使得Ai0(z)為無窮型,但由定理條件可知,無窮型的系數至多只有一個,于是由定理D可得,方程(1.3)的每一個非零解都滿足ρ(f)≥ρ+1,這都得到了矛盾. 現假設定理的結論不成立,即存在θ0∈[?π,π),有max{hAi(θ0):i∈D(n)}>0且對于任意s,k∈D(n),要么 要么 注意到不管是(3.1)式成立還是(3.2)式成立,都必定存在s0∈D(n)使得下式成立 于是由引理1便知存在至多n個零測集Ei(0≤i≤n,i≠s0),對于任意 都能找到R0=R0(θ)>1,使得當|z|=r≥R0時,有 其中w0=0.由于Ai(z)(i∈D(n))都是有限型,故hAi(θ)(i∈D(n))都是連續函數.注意到是一個零測度集,結合(3.3)式便知存在使得下列不等式成立 同時,改寫方程可以得到 于是由引理2可得 這與(3.5)式矛盾. 如果 δ≤ 0.對于 ?i∈ D(n)?{s0},j∈ {0,1,2,···n}?D(n),設 則存在點列rm使得 根據引理3可得 不等式右邊第二項移到左邊,整理后得 由于hAs0(θ1)?ε>0和ρ>ρ(f)?1+ε,于是當rm充分大時,有 兩邊取對數并注意到δ≤0,故有 定理1.2的證明 現假設定理的結論不成立,即存在θ0∈[?π,π),對于任意s,k∈D(n),要么 要么 注意到不管是(3.6)式成立還是(3.7)式成立,都必定存在s0∈D(n)使得下式成立 和 成立.設δ=max{hAi(θ1):i∈D(n)},若δ>0,證明方法完全類似于定理(1.1). 若 δ≤ 0,?i∈ D(n)?{s0},設則存在點列rm使得 根據引理3可得 注意到δ≤0,結合(3.9)式便有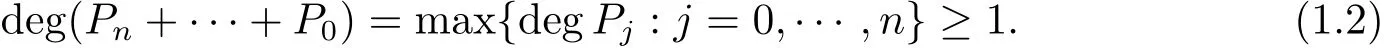
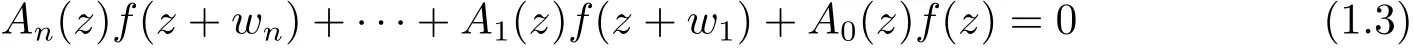
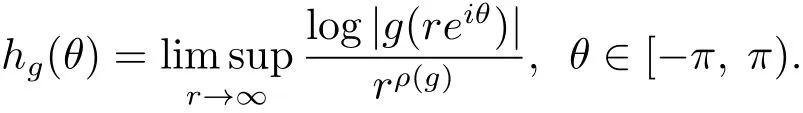


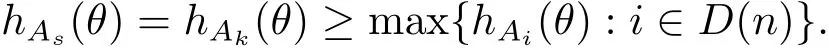
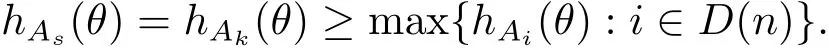
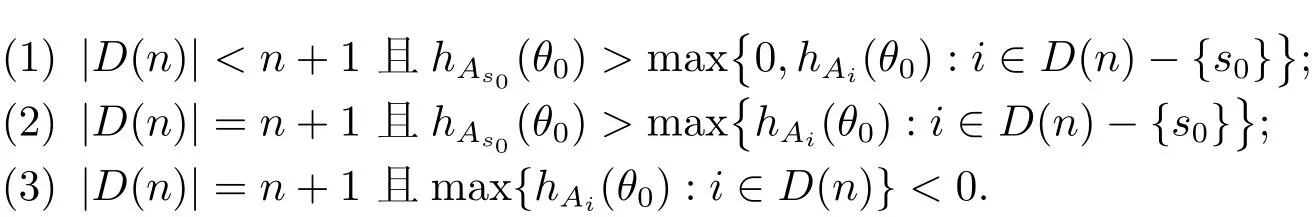
2 引理

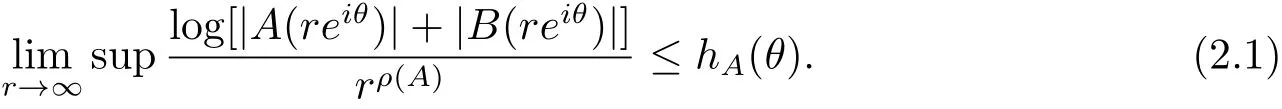
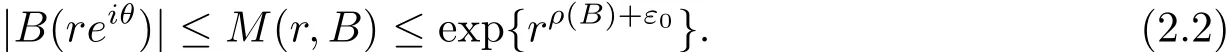
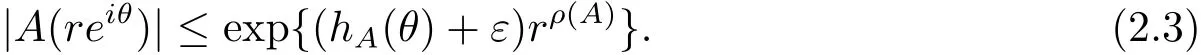
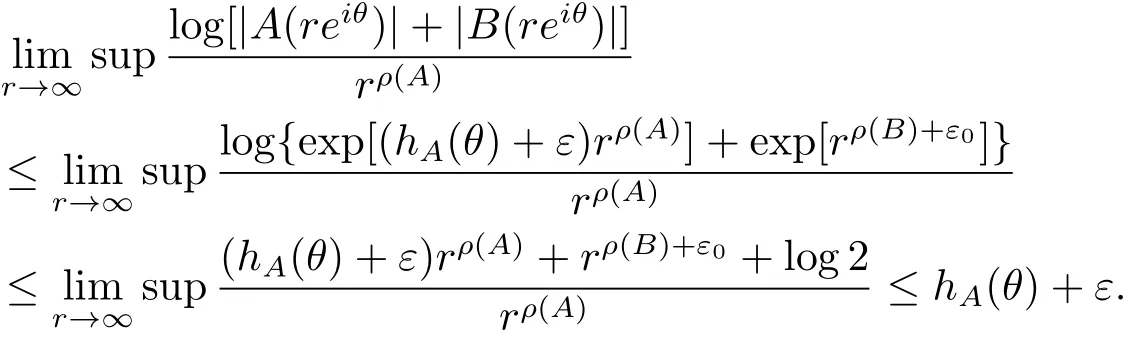
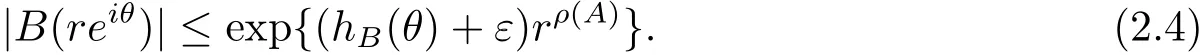
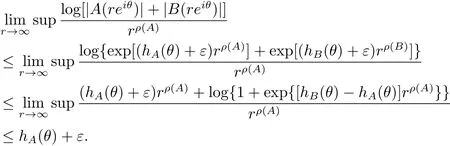
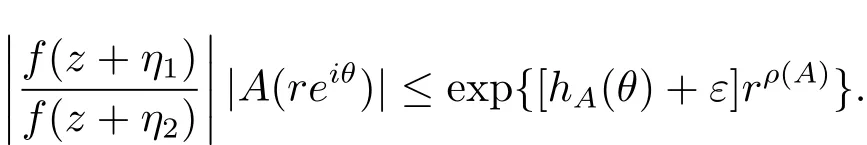
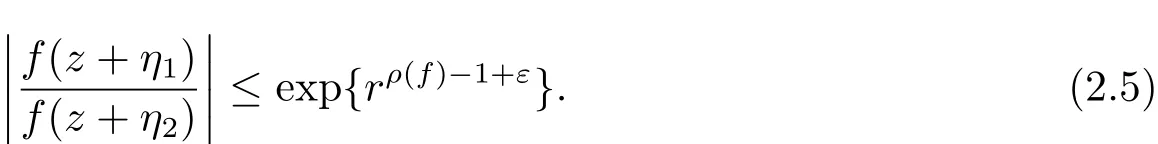
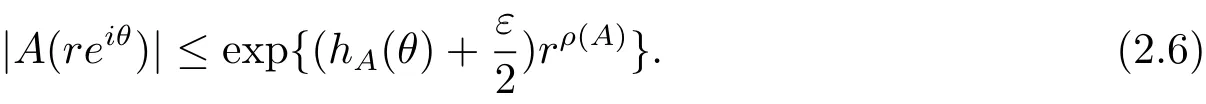
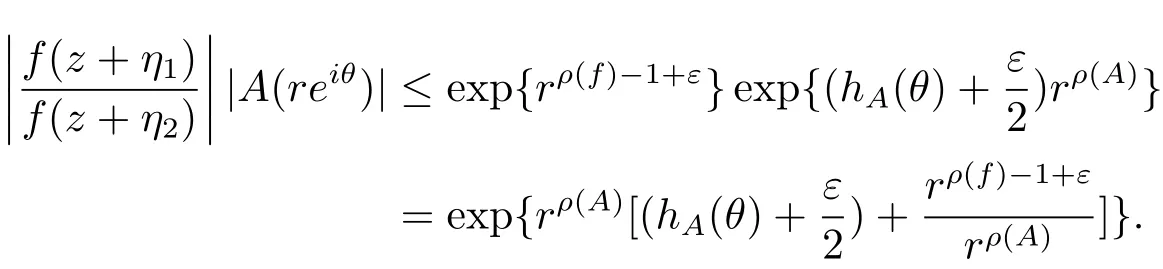
3 定理的證明