淺談在規律探索教學中培養學生的思維能力

摘 要：小學數學中的“圖形變化規律”“數列變化規律”和“操作活動變化規律”都是活動性、探索性比較強的“探索規律”內容，教師要在“數”“式”“形”的規律探索教學中，培養學生的思維能力。

關鍵詞：探索規律；數學教學；思維能力

一切規律的探索，歸根結底是方法的探索。探索規律是一個發現關系、發展思維的過程，有利于學生夯實基礎，開拓創新，更能夠體現數學思考過程，凸顯過程與方法。同時，也能夠讓學生在自主探索與思考中感受到學習的快樂，形成積極的學習情感與態度。小學數學中的“圖形變化規律”“數列變化規律”和“操作活動變化規律”都是活動性、探索性比較強的探索規律內容，教師要充分激活學生已有的知識經驗，引導學生從不同角度探索規律，總結方法，讓學生在探索規律的過程中培養思維能力。

一、在“數”的規律探索中培養學生的思維能力

小學低年段的規律探索內容大部分以“數”的規律探索為主。在探索數的規律時，我們首先應從題目所提供的數字入手，尋找不變的量；然后將所給的每個“數”化成有規律的式子，尋找變化的量；接著研究變化的量如何變化，歸納出規律，得出一般性的結論；最后，對于獲得的結論，進行驗算或證明它的正確性。通過探索“數”的規律，發展學生的合情推理能力。例如按規律填空：

（1）6、9、12、15、（ ）。

（2）12、5、14、5、16、5、18、5、（ ）、（ ）。

（3）5、21、10、19、15、17、（ ）、（ ）。

在解題時首先引導學生細心觀察，采用或挨著找，或隔著找，或連著找的方法，我們不難發現（1）式的規律是后一個數等于前一個數加3；（2）式的規律是兩數之間有一個固定數是5，而這兩個相隔的數是越來越大的連續偶數；（3）式的規律是第一個相隔數是5的倍數，第二個相隔數是越來越小的連續奇數，從而得出（1）式的括號里應填18，（2）式的括號里應填20、5，（3）式的括號里應填20、15。當然不要忘了對所得出的規律的正確性進行驗算。

二、在“式”的規律探索中培養學生的思維能力

小學中年段的規律探索內容大部分以“式”的規律探索為主，并安排為獨立的學習內容。在探索“式”的規律時，教師首先引導學生觀察有規律的代數式或等式；然后引導學生在這些有規律的式子中，尋找不變的量和變化的量，并研究變化的量如何變化，在實驗、猜測的過程中找出規律，同時加以證明，并用字母表示。讓學生經歷觀察、實驗、猜想、證明等數學活動過程，培養學生的初步演繹推理能力。

例如，人教版四年級下冊運算定律單元中的加法運算定律教學，原題是：李叔叔準備騎車旅行一個星期，今天上午騎了40km，下午騎了56km。李叔叔今天一共騎了多少千米？有的學生列式40+56=96，有的學生列式56+40=96，學生通過觀察得出40+56=56+40。然后讓學生再舉出幾個這樣的例子，并進行大膽猜測：兩個數相加，交換加數的位置，和不變。這個發現是否正確，需要我們去驗證。接下來便要求學生舉例驗證：給大家30秒時間，你能寫出幾個就寫幾個，并把你舉的例子和大家分享一下。同時啟發思考：從我們舉的例子來看，是否有交換兩個加數的位置后，和會發生變化的？ 找不到反例，證明大家的猜想是正確的。最后，引導學生用自己喜歡的圖形、符號、字母等代表兩個加數，把加法交換律既簡單又清楚地表示出來。

三、在“形”的規律探索中培養學生的思維能力

小學高年段的規律探索內容大部分以“形”的規律探索為主。主要類型有：形狀一樣但顏色不同的多個幾何圖形的圖案問題，圖形的折疊、旋轉問題，同一種圖形大小不一的排列問題，同一種圖形的數量變化問題及數字與幾何圖形的有機結合排列等問題。此類規律通常以確定探索物體的個數和確定圖形數量為主要內容出現的。

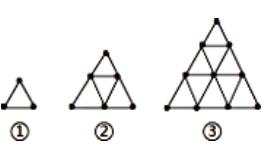
例如：用火柴棒按下面的方式搭圖形，填寫下表并回答問題：

①第n個圖形的大三角形周長的火柴棒是幾根？

②第n個圖形的小三角形個數有幾個？第200個圖形的小三角形個數有幾個？

圖形編號 ① ② ③ ④

大三角形周長的火柴棒根數 3 6

小三角形個數 1

探索物體的個數時，可首先求出各圖中物體的個數，然后將其與相應的圖序數做對比，看兩者有何關系，可得規律；或者求出各圖中物體的個數后，問題的研究就由形轉化成了數，只要研究數字規律即可得到圖形規律。可知第①問的規律是：大三角形周長的火柴棒根數=圖序數×3，所以第n個圖形的大三角形周長的火柴棒是3n根；第②問的規律是：小三角形個數=圖序數的平方，所以第n個圖形的小三角形個數有n2個，第200個圖形的小三角形個數有2200個。

總之，探索規律的學習應根據學生的年齡特征和數學知識發展的邏輯順序，從一年級開始，由淺入深、循序漸進地進行安排，使學生在探索規律的過程中逐步提升思維，培養學生解決問題的探索性和靈活性。

作者簡介：李鵬輝（1971— ），中小學一級教師，福建省農村骨干教師，龍巖市骨干教師，長汀縣名師。