中職數學教學中的情境創設

陳立斌

摘 要：中職數學是中職學校重要的文化基礎課，是學好專業課的基礎。然而，中職學生普遍數學基礎知識薄弱，對數學學習缺乏興趣。本文就如何提高中職數學教學效果，激發學生學習數學的興趣，從教學情境創設方面，談談自己的教學經驗。

關鍵詞：中職數學；教學情境；措施

中職學生普遍文化課基礎薄弱，尤其數學知識比較缺乏，不僅表現為數學知識掌握不扎實，而且對數學學習缺乏興趣。要想提高中職學校的數學教學效果，培養學生對數學的學習興趣很重要。課堂是教學的主陣地，每一次課堂教學都是從情境創設開始的，有效的情境能夠激發學生學習數學的興趣。筆者結合自己在中職數學教學工作中的經驗，談一談中職數學教學中創設情境的方法。

一、以數學游戲創設教學情境

數學游戲是一種運用數學知識的大眾智力娛樂活動，把有趣的數學游戲引入數學教學中，在具體的情境中初步認識對象的特征，用游戲激活課堂。

例如，在“兩條直線的位置關系”一課的教學，教師可以讓學生玩“兩人的雙手各被兩根繩子交叉綁住，不解開繩子或剪短繩子，將兩人分開”的游戲，讓學生發揮自己的想象力尋找解決方案。學生經過努力未能解決這個問題，會向教師尋求幫助，這樣就把學生的注意力拉回了課堂。學生在教師的指導下，成功解決問題，體會到成功的喜悅，從而激發了學生學習的興趣。教材上的概念、性質，多是以較抽象的結論或精煉的數學語言呈現的，學生理解起來會有一定的困難，而游戲的方式可以改變知識的呈現方式，利用學生頭腦中已有的知識或相關經驗，為學習提供有利條件。

二、以數學故事創設教學情境

數學理論的發展史中，數學故事豐富多彩，把數學故事引入課堂中，極大地豐富了數學教學內容，激發了學生學習的積極性。因此，在數學教學中適當結合數學故事有利于培養學生對數學的興趣，幫助學生克服消極傾向。

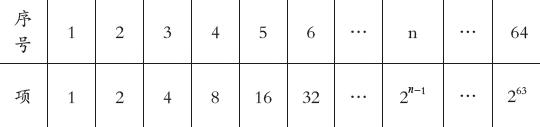
例如，在“數列”一課的教學，引入國王與麥粒的故事。國王要獎勵國際象棋的發明者，讓發明者自己提出獎勵要求，發明者提出的要求是：“請在棋盤的第1個格子里放1顆麥粒，在棋盤的第2個格子里放2顆麥粒，在第3個格子里放4顆麥粒，在第4個格子里放8顆麥粒，以此類推，每個格子里放置的麥粒都是前一個格子的2倍，直到第64個格子。”國王聽了很高興，覺得這太容易了，你覺得國王是否真的滿足發明者的要求？學習了數列知識后，學生就可以幫助國王回答這個問題。從棋盤第1個格子到第64個格子的麥粒：

從棋盤第1個格子到第64個格子麥粒的總數：Sn=1+2+4+8+16+…+…+263=18446744073709551615。一斤麥子有26000粒麥粒，那么18，446，744，073，709，551，615÷26，000÷2000=354，745，078，340.568 （噸） 。

這是一個非常有趣的數學故事，包含了等比數列的公比、首項、通項公式、等比數列求和等數學知識。學生在感受數學故事的同時，又學到了數學知識。

三、以數學歷史創設教學情境

數學是一門古老的學科，歷史悠久，源遠流長。中國古代的數學家為數學的發展創立了豐功偉績。成書東漢時期的《九章算術》是中國古代最早的數學著作，隨后出現了祖沖之、秦九韶公式（國外稱海倫公式）等，這些都比西方數學早幾百年。把數學歷史引入數學教學中，將會激發學生的愛國主義情懷，樹立民族自豪感。

四、以數學實驗創設教學情境

數學實驗就是教師依據學生的實際能力，結合教材知識，運用一定的教學道具和手段，引導學生積極實驗，并且在教學過程中組織學生主動獲取知識和構建知識，培養其數學思維、數學技能和數學素質。

例如，在“指數函數”教學中，教師可以讓學生完成關于折紙的實驗。

師：誰能告訴我珠穆朗瑪峰有多高？

生：大約8848米。

師：那么大家有沒有想過一張紙經過有限次對折之后厚度會達到甚至超過珠峰的高度呢？下面我們來分析一下這個問題，將一張紙從中間對折，設對折次數為x，對折后紙的層數為y，y與x之間構成一個函數關系，你們能寫出x與y之間的函數關系式嗎？

生：y與x之間的關系式可以表示為：y=2x。

師：借助計算機算一下，當紙的厚度為0.03mm時，對折32次，它的厚度能達到多少？會超過珠峰嗎？

生：當x=32時，y=4294967296，超過了珠峰的高度。

這個實驗把指數函數的相關知識融入其中，學生通過全程參與實驗，從函數關系式的建立到得出對折32次紙張的厚度，最終的結果讓學生匪夷所思，感受到數學知識的博大精深，從而激發學生學習數學的興趣。

要想提高中職學校的數學教學效果，首先要吸引學生，激發學生學習數學的興趣。中職數學教師要在創設教學情境上多下工夫，把學生的注意力吸引到課堂教學上來，培養學生學習數學的興趣。興趣是最好的老師，只要學生有了學習興趣，中職數學教學工作一定能圓滿開展，達到預期效果。

參考文獻：

[1]鮑分民.運用數學游戲激活課堂[J].考試周刊，2013（84）.

[2]畢偉華，唐艷敏.基于數學故事在中學數學中的實踐應用研究[J]. 數學學習與研究（教研版），2017（7）.