“數學思考”教學如何引向深入
———“數學思考”教學片斷與評析

執教/ 陳光明 評析/ 陳華忠(特級教師)

片斷一：創設情境，提出問題

教師與兩位同學兩兩握手。

師：剛才我們三個人一共握了幾次手？

生：3次。

師：如果相互握手的人一共有4個，將一共要握幾次手呢？

生 1：4次。

生2：不對，應該是6次。

師：怎么會是6次呢？你能用什么方法使我們相信你的結論。

（生2在黑板上畫圖說明）

師：剛才這位同學用4個點代表4個人，用4個點之間的連線表示他們之間相互握手。這是一種很了不起的方法。我們通常稱之為“數形結合”。

師：猜一猜，紙上的任意8個點，一共可以連成多少條線段？

生1：8條。

生2：24條。

生3：16條。

生4：28條。

師：大家來驗證一下，你們猜得對嗎？請大家拿出紙和筆在紙上任意點上8個點，并將它們每兩點連成一條線，再數一數，看看連成了多少條線段？

師：有結果了嗎？

生：太亂了，都數昏了。

師：別急，今天我們就一起來用數學的思考方法去解決這個難題。（板書課題:數學思考—化難為易）

【評析：先讓學生猜一猜任意8個點，一共可以連成多少條線段？然后讓學生進行驗證，看似簡單，連線時感覺很亂也很容易出錯。這樣在課前制造一個懸念，不僅激發學生學習的欲望，同時又為探究“化難為易”的數學方法埋下伏筆。】

片斷二：自主探究，尋找規律

1.從簡到繁，動態演示，經歷連線過程。

師：用8個點進行連線，大家覺得有些麻煩也很亂，應該怎么辦呢？

師：有什么好辦法嗎？

生1：如果把點減少一些，就會容易一些。

生2：先從2個點開始，逐步增加點數，尋找其中的規律。

師：好的，我們就從簡單的2個點入手，逐步增加點數，找一找有什么規律？

1.學生獨立研究點數是2～6的情況。并發現其中的規律。

?

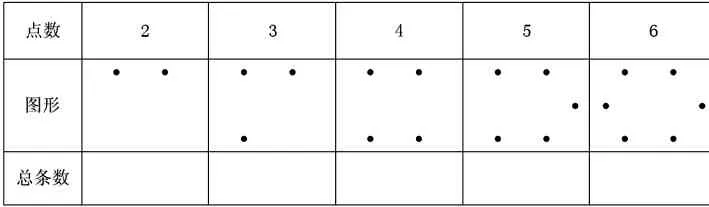
師：大家認真觀察、對比分析，思考增加線段與點數的關系。

師：仔細觀察這張表格，在這張表格里有哪些信息呢？看著這些信息你有什么發現嗎？

生：每次增加的線段數和點數相差1。

師：當3個點時，增加條數是幾？

生：2條。

師：那點數是4時，增加條數是多少？

生：增加3條。

師：點數是5時呢？

生：增加4條。

師：點數是6時呢？

生：增加5條。

教師小結：我們可以發現，每次增加的線段數就是（點數－1）。

師：數學的探究可不是得出結論就結束了。我們更應該探究結論背后的原因。為什么“每次增加的線段數就是（點數－1）”呢？

（學生同桌討論，再讓學生在班上交流，并結合課件，使學生明白：“因為每增加一個點都要和原先的所有點連一條線。”）

【評析：在經歷了豐富的連線過程之后，引導學生從整體上進行觀察、分析與比較表格中的線段與點數，逐漸增加點，從中發現每次增加條數就是點數－1，為后面推導總線段數的算法做好鋪墊。】

2.進一步探究，推導總線段數的算法。

（1）分步指導，逐個列出求總線段數的算式。

師：大家知道了5個點可以連10條線段，現在你們有什么辦法知道6個點、8個點可以連多少條線段嗎？

生：連一連，算一算。

師：（追問）如果當點數再多一些時，我們這樣去計算是不是很麻煩呢？看看它們有沒有什么規律，行嗎？

師：我們先來看，2個點連1條線段，那么3個點時，可以連多少條線段？你是怎么知道的？

生：2個點連1條線段，增加一個點，就增加了2條線段，1＋2＝3（條），所以3個點就連了3條線段。

師：4個點共連了6條線段，這又可以怎么計算呢？

生：計算3個點連出的線段數時，我們用了1＋2，再增加1個點，就增加了3條線段，我們就再加3，所以列式為 1＋2＋3＝6（條）。

師：那么按著這個方法，你能列出5個點共連線段的算式嗎？

生：1＋2＋3+4＝10（條）。

（2）觀察算式，探究規律。

師：大家仔細觀察這些算式，有什么發現嗎？

生1：計算3個點的總線段數是1＋2，計算4個點的總線段數是1＋2＋3，計算5個點的總線段數是1＋2＋3＋4，它們都是從 1 開始依次加的。

生2：我覺得計算總線段數其實就是從1開始加2，加3，加4，一直加到比點數少1的數。

師：那么你說的點數少1的那個數其實是什么數？

生：就是每次增加一個點時，增加的線段數。

（3）引導小結，歸納規律。

師：現在我們只要知道點數是幾，就從1開始，依次加到幾減1，所得的和就是總線段數。同學們，明白了嗎？

師：下面我們運用這條規律去計算一下6個點和8個點時共連的線段數，請同學們把算式寫在作業紙上。

（學生獨立完成，教師巡視，之后學生板演算式集體評議）

師：如果是n個點，該如何列式？

生：1+2+3+…+（n-1）=n（n-1）÷2。

【評析：在探討總線段數的算法時，同樣延用從簡到繁的思考方法，讓學生觀察發現這些算式的共有特征：都是從1依次加到點數減1的那個數，從而讓學生明白總線段數其實就是從1依次連加到點數減1的那個數的自然數數列之和。接著讓學生用已建立的數學模型去推算6個點、8個點時一共可以連成多少條線段。若有n個點，讓學生進行拓展引伸，歸納出可連接n(n-1)÷2條線段，這是數學思考在這節課中的一個升華。也是從特殊到一般的規律的探究。】

片斷三：變換問題，建立對應

師：將6個點移到同一條直線上，這6個點能決定多少條線段？

生：6×5÷2=15。

師：與例題中的問題有什么聯系？

（建立“一一對應”）

師：將同一直線上的六個點與直線外一點依次連接，圖上有幾個三角形？

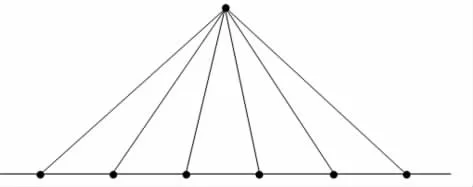
師：你是如何思考的？

師：還能像這樣繼續改變題目，通過“一一對應”尋找答案嗎？

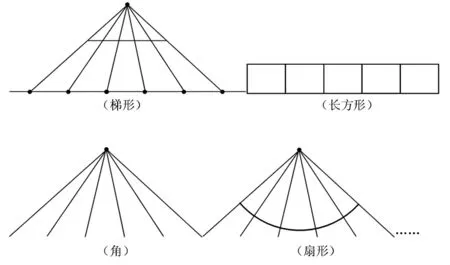
【評析：經歷豐富的連線過程，引導學生通過觀察、分析與比較，從而進一步發現規律，再通過變式訓練與例題中的問題建立了“一一對應”的聯系，使學生懂得運用一定的規律去解決較復雜的數學問題，提高學生解決問題的能力。也滲透轉化與化難為易的數學思想與方法，】

片斷四：運用規律，解決問題

師：在上課開始，大家就發現連線問題和握手問題直接的聯系。如果我們班的全體同學每個人之間都握一次手，總共要握多少次手呢？該如何列式？

師：生活中還有哪些問題和今天的“連線問題”相類似？你能提出這樣的問題嗎？

生1：單循環賽問題。

生2：從我們小組中推選兩位組長，一共有多少種方法？

生3：在幾個城市之間開辟航線，一共需要開辟多少條航線？

【評析：運用所學知識，解決日常生活中的實際問題，讓學生感受到數學源于生活，又服務于生活，產生要學好數學的情感體驗。】

【總評：《數學思考》是總復習的例題。實質上就是通過尋找規律來解決實際問題。這里的規律的一般化表述是：以平面上幾個點為端點，可以連多少條線段。即例1：“6個點可以連成多少條線段？8個點呢？”這種以幾何形態顯現的問題，便于學生動手操作，通過一邊畫圖一邊探究，有利于學生對化歸、數形結合和化繁為簡等數學思想方法形成系統的認識。

1.由淺入深，深化學生的數學思考。

柏拉圖說：“我們應該區分兩種不同的存在——經驗的存在和理性的存在。經驗的存在是有缺陷的，理性的存在才是完美的。”教學中，遇到復雜的問題，我們往往采取化難為易的方法，先從簡單問題去思考，逐步找到其中的規律，再用規律去解決復雜的問題。本節課教材中呈現的探究方法是：從簡單問題即兩個點開始，逐個增加點數進行探討，去找尋其中的規律。這樣，還不能讓學生體驗到從無序到有序、從雜亂中找到規律的思維過程，從而引導學生用每一個點與其他點分別相連，并尋找其中的規律。即當3個點時，增加條數是幾？（生：2條）點數是4時，增加條數是多少？（生：3條）點數是5時呢？（4條）6時呢？（5條）引導學生發現，每次增加的線段數就是（點數－1）,總線段數其實就是從1依次連加到點數減1的那個數的自然數數列之和。為此，只要知道點數是幾，我們就從1開始，依次加到幾減1，所得的和就是總線段數。這樣，有利于學生對數學思考中的條理性與有序性的認識，更利于學生清晰感受化難為易等數學思想方法。這樣，不僅激發了學生的學習欲望，同時又為滲透“有序思考”和“化繁為簡”的數學思想方法埋下伏筆。

2.由點到面，促進學生的數學思考。

學生從一個個具體的點向知識的面匯聚的過程，也是學生思維從具體向抽象生長的過程。在這一過程中學生的數學思考由點到面不斷生長，思維能力不斷提高。本節課中教師采用從簡到繁的思考方法，依托課件先探究2個點時連成一條線段，之后列出3個點、4個點、5個點……讓學生通過一邊畫圖一邊探究，并引導學生觀察,當3個點時，增加條數是幾？點數是4時，增加條數是多少？點數是5時呢？ 6時呢？這樣，學生就會有新的發現，再引導學生通過不完全歸納，讓學生觀察發現這些算式的共有特征：都是從1依次加到點數減1的那個數，線條數=1+2+3+……+（點數-1），并歸納出公式為：線條數=點數×（點數-1）÷2。這樣，學生在探究中發現、建立基本計算線條數的模型，體驗到探究的快樂與成功感，真正實現了在探究中學有所樂，在快樂中學有所獲，同時也促進學生進行數學思考。

3.由定到變，激活學生的數學思考。

在數學教學中，我們需要培養學生數學思考的有序性與條理性，也要培養學生解決問題的靈活性與多樣性，從有序的“規定”到看似無序的“變化”，往往能激發學生的認知沖突與解決問題的欲望。學生在這種心求通而不能，口欲言而弗達的“憤悱”之中，思維的火花被點燃，主動積極思考成為可能。本節課中教師先引導學生思考并探究“6個點可以連成多少條線段？8個點呢？”再到n個點可連成多少條線段？然后通過變式將6個點移到同一條直線上，這6個點能決定多少條線段？再變成將同一直線上的六個點與直線外一點依次連接，圖上有幾個三角形？并延伸出可以找出幾個扇形？幾個角？還可以從幾個長方形到用幾條小棒等。通過不斷地變式訓練，引導學生積極思考，不斷探究，有利于激活學生的數學思考。】