凸顯思維過程 開發(fā)智力潛能
——《新思維兒童數(shù)學》（1A）實踐感悟

王國宏 俞 波

優(yōu)質(zhì)的教材是培養(yǎng)優(yōu)秀人才所使用的材料，是實現(xiàn)教學目標的載體。2017年，中國科學院心理研究所特邀研究員、浙江省功勛教師張?zhí)煨⑾壬ば木幹⑼瞥隽恕缎滤季S兒童數(shù)學》系列讀本。從2017年9月開始，杭州地區(qū)進行了首輪實踐和實驗。我們有幸成為研究團隊的成員，在進行了一個學期的實踐和研討后，深刻體會到1A冊讀本靈活、多樣、獨特、關聯(lián)的編寫特點，是現(xiàn)行各種版本教材內(nèi)容很好的補充和數(shù)學教師進行數(shù)學思維訓練的范本，能有效地提升學生的數(shù)學素養(yǎng)。

一、創(chuàng)新基礎，有利于學生學會學習、學會思考

1A冊第三單元中，張老師安排了一節(jié)特別的概念課——《翻倍與折半》，這是其他教材沒有的內(nèi)容。我們在請教新思維教研團隊后了解到翻倍與折半是解決很多典型數(shù)學問題的重要基礎，如“和差問題”：兩個數(shù)的和是a，差是 b，求較大數(shù)，就是（a+b）折半，求較小數(shù)，就是（a－b）折半；又如“差值等分”問題：大筐有12個梨，小筐有4個梨，從大筐里拿出幾個放到小筐，兩筐梨一樣多？需要將兩筐梨的相差數(shù)折半；……

這樣的教學內(nèi)容學生能不能學會呢？我們仔細推敲材料，發(fā)現(xiàn)張老師的設計實在是太巧妙了，他以多元表征的方式呈現(xiàn)翻倍與折半的內(nèi)涵，非常有利于學生獲得概念。

“圖像”表征翻倍與折半：

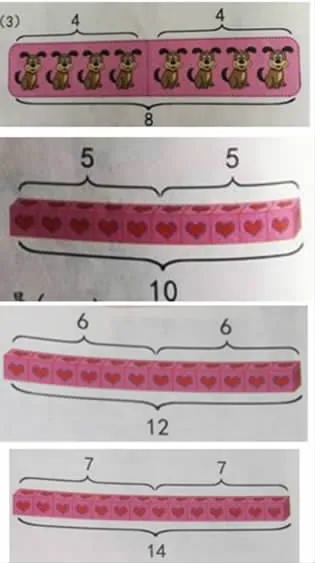
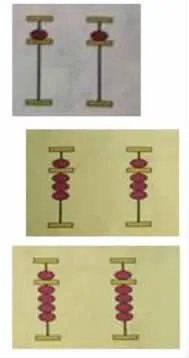
“數(shù)形結(jié)合”表征翻倍與折半：

“語言”表征翻倍與折半：

20是（ ）的翻倍；20折半是（ ）。5是（ ）的折半；5翻倍是10。

筆者對這節(jié)課進行了課堂實踐，發(fā)現(xiàn)其內(nèi)容、情境、序列都非常合理，教師教學時只要按照教材設計實時展開、適當調(diào)控，就能很自然地啟發(fā)學生獨立思考，逐步深入。當我們要求學生用一句話來總結(jié)本課的學習體會時，有的學生說：“老師，折半和翻倍是一對好兄弟，一元錢折半是五毛錢，五毛錢翻倍是一元錢。”有的學生說：“老師，我想讓我們的綠色植物不斷翻倍、變多，這樣我們的環(huán)境就能越來越好了。”馬上有個學生仿照說：“老師，我想讓我們的困難不斷的折半、減少，這樣我們就會更加開心了！”學生的活學活用令人驚喜！

二、開放課堂，幫助學生體驗成功、感受快樂

教材第二單元中《認識立體圖形》一課，經(jīng)我們與人教版的相關內(nèi)容對比，浙教教材中更注重將各種立體圖形與生活原型相聯(lián)系，包括在具體物品中抽象出立體圖形與基于立體圖形發(fā)散想象具體物品。因此，在教學處理上，強調(diào)學生要結(jié)合自己已有的生活經(jīng)驗來理解、概括這些圖形的特征。

《新思維兒童數(shù)學（1A）》

“立體圖形”教材頁面

王國宏老師執(zhí)教了這節(jié)課，在說下課的時候，很多學生還不想下課，有一位學生站起來問王老師：“老師，我認為你說的圓柱體站著時可以叫圓柱體，如果平放在桌面上，我想叫它‘圓滾體’，您認為可以嗎？”王老師追問：“你為什么想叫它圓滾體呢？”這位小女孩大膽地說出了自己的想法，她說：“通過剛才的玩一玩，我看到這五種立體形狀的物品平放在桌子上，球是向四面八方滾動的，而圓錐體是圍繞一個點滾動的，只有圓柱體是向一個方向滾動的，我覺得叫圓滾體讓我一下子想到了它特別的地方。”王老師馬上表揚這位說出這些圖形在滾動時不同特征的學生，又引導學生想象：“如果老師從下往上，水平地去切這些圖形，切得的平面圖形有什么變化？”學生總結(jié)得出：從下往上每個截面都一樣的，叫柱體；越切越小，直到一個點的，叫錐體。王老師問：“現(xiàn)在，你們覺得圓柱體和圓滾體哪個名字更好呢？”剛才提問的同學自己站起來說：“原來“柱體”和“錐體”也有特別的意思。我們還是叫它圓柱體吧！”

這個案例使我們深刻理解到有意義的學習是解放學生的學習，有意義的課堂是開放的課堂。在這樣的課堂里，學生有機會用自己的方式去了解、理解各種概念、規(guī)則，可以安全、自如地表達自己的思考、見解，體會到自主學習的權(quán)利和成功的快樂，心悅誠服于邏輯、道理。

三、不求易、不避難，培養(yǎng)數(shù)學學習的良好品格

第一單元中《幾加幾》一課內(nèi)容獨特，難度系數(shù)不小。根據(jù)教材，杭州市賀知章小學的許老師是這樣展開教學的。

（一）探究等式

1. 感知“＝”的含義。

（1）列一列。

請你找一找1～9這些數(shù)中哪兩個數(shù)相加和是9？

根據(jù)學生發(fā)言，形成板書：

4+5＝9 3+6＝9

2+7＝9 1+8＝9

（2）找一找。

引導學生觀察四個加法算式，發(fā)現(xiàn)排列規(guī)律。

看算式：第一個加數(shù)一個一個減少，第二個加數(shù)一個一個增加。

看圖像：左右對稱，大數(shù)配小數(shù)。

2.構(gòu)建等式。

4+5＝3+6 4+5＝2+7

4+5＝1+8 3+6＝2+7

3+6=1+8 2+7=1+8

（二）自主探究

1.請你寫出兩個數(shù)相加和是7的算式，看誰寫得又對又好。

2. 從 1、2、3、4、5 中選四個數(shù)，使兩兩相加的和相等。

當時許老師班里共有42名學生，其中35名是外來務工人員子女，應該說學生基礎比較薄弱，但課后測試顯示，班級正確率高達93%。

經(jīng)過對執(zhí)教教師、受教學生的訪談我們豁然開朗。這個內(nèi)容本身確實有一定的難度，但是依照張?zhí)煨⒗蠋煹摹缎滤季S兒童數(shù)學》序列化地訓練之后，學生在思考的系統(tǒng)性和靈活性上有了很大的變化，充分體現(xiàn)出對關系的關注、規(guī)律的敏感、數(shù)形結(jié)合的認知方式、有序地思考等等。同時，學生更樂于接受有一定難度的問題挑戰(zhàn)，更能沉下心來長時間思考、作業(yè)，不求易、不避難，有著良好的意志品格。

學者成尚榮指出：當下的教育在不知不覺中小心翼翼地為自己畫了一個圈、筑了一堵墻，這個圈、這堵墻的名字叫做現(xiàn)實性，教育只關注學生的現(xiàn)實性且時時緊盯著學生的現(xiàn)實性，始終沒有勇氣探出頭來看看墻外有沒有更廣闊的天地和更美麗的風景，這個墻外的風景和天地正是學生的可能性。

《新思維兒童數(shù)學》（1A）就為學生的數(shù)學學習提供了很多的可能性。全書著眼于高層次思維的培養(yǎng)，體系縝密、題例豐富、思想方法循序漸進、螺旋上升，如果能夠系統(tǒng)使用，發(fā)展學生數(shù)學思維的效果是十分顯著的。當然，我們一線教師也可以配合自己的教學進度有選擇地使用，以達到拓展學生思維的功效。