自主探索為基石 方法引領為階梯
——《梯形面積》教學實錄與評析

執教/趙姝蓉 指導/姜榮富

【教學內容】

浙教版五年級。

【教學過程】

一、回顧舊知，引入新知

師：還記得我們是用什么方法研究平行四邊形面積的計算公式嗎？那么三角形面積該怎么研究呢？

師：如果將三角形面積的研究方法分為兩類，可以怎么分？

生：分為倍拼和割補兩類。

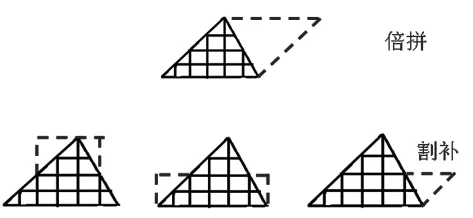
師：雖然轉化的方法不同，但都是轉化成學過的平行四邊形或長方形來研究的。

師：（出示一般梯形）今天我們一起來學習《梯形面積》一課，根據你們以往的學習經驗，可以把梯形轉化成什么圖形？

（學生獨立思考，發言）

【評析：導入部分回顧了平行四邊形和三角形面積計算公式的探究方法，一方面梯形面積計算推導時要用到平行四邊形和三角形的面積計算公式；另一方面，“轉化”的思想是一脈相承的。將三角形面積探究的方法類化為倍拼和割補兩種方法，“類化”對于梯形面積計算公式的探究是重要的鋪墊。通過知識聯系和方法類化，為后繼學習積累經驗，打好基礎。】

二、動手操作，自主探究

1.獨立操作，教師巡視。

師：老師在材料包里準備了一些梯形，請根據自己的想法轉化成學過的圖形。

（學生獨立剪拼研究）

2.小組交流，準備匯報。

（1）說說自己是怎樣轉化的。

（2）補充別人沒有的方法。

（3）推選代表進行匯報。

3.匯報方法，全班展示。

（學生展示剪拼的方法）

預設：②③④⑥⑧這些方法是學生比較容易出現的；沒有出現的①⑤⑦⑨這些方法，可以電腦展示。

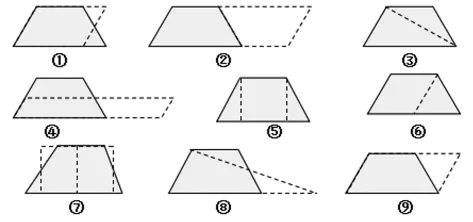
師：轉化后圖形的面積和原來梯形的面積有什么關系？

（倍拼的面積是原來梯形面積的兩倍，其余的和原梯形面積一樣，第9種例外）

師：轉化后的哪一種圖形最容易算出它的面積？

生：倍拼的圖形最容易。

【評析：在這個環節，不給出具體的數據更加能突出圖形轉化的重點，學生通過獨立操作，研究、展示出各種轉化方法。其中一部分是很容易看出如何轉化的，也有一部分是不容易看出來的。對于不容易看出來的，請學生談談想法，相互交流，互相啟發，使其方法多樣化。】

4.計算面積，歸納公式。

師：你能算出②號平行四邊形的面積嗎？

生：不能，沒有數據。

師：如果只給你梯形的數據，行嗎？（行）那你們覺得需要梯形的哪些數據呢？

（教師給出數據：上底3、下底 7、高 4和腰 5）

師：現在怎樣計算平行四邊形的面積？怎樣計算梯形的面積？

板書：S梯=（3+7）×4÷2=20

師：這個算式里的各部分分別表示轉化后圖形的哪個部分？

生：3+7表示轉化后平行四邊形的底，4表示轉化后平行四邊形的高。

師：請從剩余的轉化方法中，選一種求轉化后的圖形面積。

（1）學生選擇數據，計算轉化后圖形的面積。

（2）反饋梯形面積計算的算式和結果。

師：觀察②④⑧這三種圖形的計算算式有什么共同點？

生：都可以整理成為S梯=（3+7）×4÷2=20。

師：通過轉化和計算發現梯形的面積與什么有關？

生：上底、下底和高。

師：通過剛才的活動，可以總結出怎樣計算梯形的面積？

生：S梯=（上底+下底）×高÷2。

師：觀察③，因為轉化后圖形的面積也是20，說明你們的方法都是正確的，只是每種算式的表達形式不同，你們能整理成這樣的表達方式嗎？

師：那么這里的（3+7）表示什么？

生：上底加下底。

師：看樣子在計算梯形面積的時候和什么無關？

生：和兩個腰無關。

（3）如果我們現在用a來表示上底、b表示下底、h表示高，你能用算式來表示梯形的面積嗎？

學生嘗試用字母表示：S=（a+b）×h÷2

（4）課外補充：展示學生沒有討論到的推理方法，鼓勵學生課后繼續研究。

【評析：給出梯形的上底、下底、兩腰和高的完整數據，由學生自己選擇有用的數據計算轉化后圖形的面積，這樣的經歷讓學生充分感受到梯形的面積計算公式與上底、下底和高有關。整體呈現轉化圖形和相應的面積算法，引導學生歸納、概括出梯形面積計算公式：S=（上底+下底）×高÷2。其中分割成兩個三角形的轉換方法，分割很容易，但是算式推導對學生有些困難，因為這里需要用到乘法分配律來提取公因數（高）。因此，我們把兩個三角形的轉換放在最后展開：第一，有了前面幾種的歸納和結果的相等，學生必然會有所猜想；第二，通過計算結果相等，也方便學生驗證推理。在學生轉化和推導的基礎上，水到渠成地提出用a來表示上底、b表示下底、h表示高，從而得到S=（a+b）×h÷2。】

三、應用公式，梳理溝通

1.出示各種梯形，填表練習。

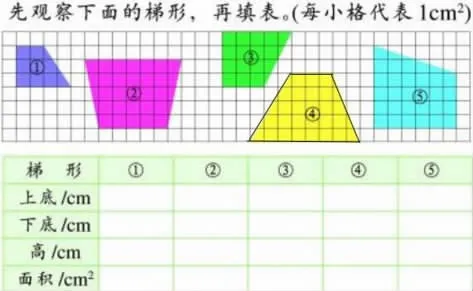
（1）獨立完成后，集體反饋。

（2）總結，強化梯形面積的計算公式。

（學生如有困惑，可以任選一個通過數方格驗證）

2.對三角形、梯形、平行四邊形面積公式進行溝通聯系。

師：今天我們研究了梯形的面積計算公式，之前我們還學習了三角形和平行四邊形的面積計算公式。它們之間有什么聯系？

（課件演示，引導學生直觀理解當 b=0 時，S=ah÷2）

師：梯形的面積計算公式和平行四邊形的面積計算公式有什么聯系？

（課件演示，引導學生直觀理解當 a=b 時，S=ah）

【評析：最后的環節沒有設計應用公式解決實際問題，還是放在數學情境內，主要是“直接應用公式”和“梳理溝通公式”。第一，應用公式求取方格圖中的梯形面積，一方面可以鞏固梯形公式，另一方面方格有助于學生將面積計算公式和面積的本義（單位面積的個數）聯系起來；第二，將平行四邊形、三角形和梯形的公式進行溝通，不僅對于單元課之間有所呼應，更重要的是，這樣的梳理溝通蘊含著“極限”的思想，為后繼學習圓面積公式的推導做準備，較好地發展了學生的空間觀念。】

【課例綜述】

雖然從整體上看這節課并沒有跳脫圖形課從問題情境——推導公式——應用公式的傳統模式，但從細節上看這節課每個環節的設計都有獨特的理解和理念在支撐，特別是充分展開公式的推導過程，甚至在練習中強調對于公式的多樣化的理解，值得品味。

1.圖形聯系，巧妙回顧。從回顧平行四邊形面積和三角形面積的探究方法引入本課，到讓學生類化三角形面積的探究方法，一方面避免了簡單的再認回憶，另一方面在眾多的方法中進行分類是一種更高層次的思維方式。這種對知識的回顧是有一定的教學增量的，也為后繼的學習做好充分的準備。

2.探索方法，分層推導。在梯形面積推導的過程中，經歷用分、合、移、補等方法探索梯形面積計算方法的過程，讓學生經歷方法的交流詮釋、轉化溝通、抽象概括過程，培養學生的邏輯思維能力，發展學生的空間觀念。對于多樣的轉化方法，從學生的角度考慮，有意識分層、分類交流與推進，很好地處理了學生自主學習和教師主導深入之間的關系。各種方法顯得多而不亂，既概括共性，生成普遍的算法 S=（a+b）h÷2，又張揚個性，不同的人對公式有不同的理解。

3.極限思想，整合溝通。通過動態的多媒體演示，滲透極限思想，把平行四邊形、三角形和梯形面積計算公式溝通整合：當b=0時，梯形轉變為三角形，面積公式為 S=ah÷2；當 a=b時，梯形轉變為平行四邊形，面積公式為S=ah。這一聯系打通了三種圖形面積之間的隔閡，溝通了算法聯系，給學生新鮮的經驗和角度。而這種用聯系的觀點看問題的思想、理念，也為學生后續的學習，特別是形成良好的認知結構奠定了基礎。