如何在初中數(shù)學教學中體現(xiàn)中小銜接

井湜

摘要：中小學數(shù)學教學的銜接是學生的數(shù)學知識和能力的銜接。搞好中小學數(shù)學教學的銜接，才能體現(xiàn)中小學數(shù)學教學的連續(xù)性和統(tǒng)一性。因此，中小學數(shù)學教學的銜接自如，是擺在教師面前的一個重要任務。此任務需要中小學數(shù)學教師的共同努力，要從小學角度考慮與中學的銜接，也要從中學角度考慮與小學的銜接。

關(guān)鍵詞：初中；數(shù)學教學；中小銜接

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2017）10-0114

筆者認為中小學數(shù)學教學銜接的角度，有教學內(nèi)容的銜接、教學方法的銜接、學習方法的銜接、學習興趣的銜接、作業(yè)書寫格式的銜接和中小學數(shù)學教師間的有效聯(lián)系等。

一、教學內(nèi)容的銜接

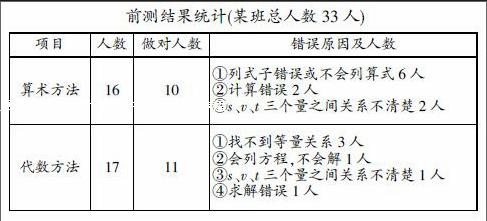
第一個銜接點是由“算術(shù)數(shù)”發(fā)展到“有理數(shù)”，小學應該為初中做好鋪墊；第二個銜接點是由“數(shù)”到“式”的過渡，七年級的“字母表示數(shù)”必須使學生清楚地知道用字母表示數(shù)是實際需要，這樣表示的數(shù)和數(shù)量既簡單明了，又具有含義的普遍性和應用的廣泛性。在計算應用題、幾何初步知識的教學中，要有意識地充分運用“字母表示數(shù)”的工具。例如，用含字母的式子表示有理數(shù)運算中的運算律、三角形面積公式的表示以及應用題中的數(shù)量關(guān)系的表示。第三個銜接點列算式解應用題到列方程解應用題的過渡。需要教師精心設(shè)計教學案，找準銜接點，放慢教學速度。例如，筆者在撰寫《列一元一次方程解應用題》的教學設(shè)計時，為了更好地進行中小銜接，首先進行了學生學情的分析。通過學情分析，從而了解到小學階段的學習，學生初步具備列簡易方程解決實際問題經(jīng)驗，并且大部分學生能夠用算術(shù)方法解決簡單的實際問題。升入初中后，又學習過字母表示數(shù)、列代數(shù)式、整式運算、等式的概念及其基本性質(zhì)、一元一次方程及其相關(guān)概念和一元一次方程的解法。而學生在列簡單一元一次方程方程解決實際問題時，能夠從實際應用問題中準確找到表示題目中的相等關(guān)系，并列出方程是學生的困難所在。同時，為了更好地了解學生小學的學習基礎(chǔ)，在授課前對學生進行了前測。前測試題選取一個既可以用小學知識列算式的方法解決，也可以用初中列一元一次方程的方法解決，目的是了解學生在解決此類問題時的思維定勢，從而打破這個思維定勢，運用多種方法解決實際問題。其中，前測試題、前測結(jié)果統(tǒng)計和結(jié)果分析如下：

前測試題：為了促進經(jīng)濟的發(fā)展，鐵路運輸實施提速。如果客車的行駛速度每小時增加40千米，提速后由北京到某地1560千米的路程只需要行駛13小時。那么，提速前客車每小時行駛多少千米？

通過前測，能夠體現(xiàn)出部分學生在小學時就會用列簡單方程解應用題，有一定的列方程解應用題的基礎(chǔ)。前測結(jié)果也說明有些問題同時可用算術(shù)方法和代數(shù)方法，然后筆者在教學設(shè)計中比較兩種方法的優(yōu)劣，使學生清晰地理解列一元一次方程解應用題的每一步，感受它直接易懂的優(yōu)越性，從而培養(yǎng)學生用代數(shù)法列一元一次方程解決應用題的能力，從而完成從算術(shù)法解應用題到代數(shù)法解應用題的順利過渡。

二、教學方法的銜接

首先教師必須結(jié)合學生的心理和生理特點，從學生的認知結(jié)構(gòu)和認知規(guī)律出發(fā)，有效地改進教法。因此，筆者在講授《列一元一次方程解應用題》一課時，以學校開展的興趣課程為情境，設(shè)計的問題都是以興趣課程為背景，這樣的目的是緊緊聯(lián)系學生的生活實際，激發(fā)學生的學習興趣。在講解時深入淺出，適當加以變式訓練，嚴格統(tǒng)一書寫格式，由小學的書寫習慣過渡為中學的習慣。同時，在講解過程中，對本節(jié)課的教學難點“尋找相等關(guān)系”做到心中有數(shù)，采取有效方法，分散難點，或化難為易，鋪路搭橋，因勢利導。利用小學畫線段圖示和中學的列表等方法，充分活躍學生的思維，正確、合理、巧妙地啟發(fā)引導學生積極思維，使學生順利達成本節(jié)課的目標，準確找到題目中的等量關(guān)系，從而列出一元一次方程求解。

三、學習方法的銜接

學習方法是做好中小銜接的關(guān)鍵。學生是學習的主體，培養(yǎng)學生自主學習的能力也就成了重點。小學階段在進行課堂小結(jié)、單元小結(jié)或是復習總結(jié)時，一般都依賴教師，習慣教師帶著去復習總結(jié)。筆者認為，從七年級開始就應該教給學生自學的方法，提升學生學會自己總結(jié)的能力。在具體指導時可以給出復習總結(jié)的途徑。要做到：一看：看書、看筆記、看習題，通過看，回憶、熟悉所學內(nèi)容；二畫：列出相關(guān)知識點，標出重點和難點，列出知識之間的關(guān)系，指導學生學習畫出章節(jié)的思維導圖，教師盡量在每節(jié)課的小結(jié)中都要用，這樣，慢慢地滲透給學生，形成學生的習慣和培養(yǎng)學生的構(gòu)造知識之間聯(lián)系的能力。三積累：在平時的作業(yè)改錯的同時，要求學生學會積累，有目的、有重點、有選擇地積累一些“好題”。“好題”都來自于平時的作業(yè)及例題，主要是一些方法特殊，方法多樣和知識含量多的題目，要求學生在積累的時候重在本題所用知識、解題方法和解題技巧的積累。這種習慣的養(yǎng)成，能充分發(fā)揮學生學習的主動性。

四、學習興趣的銜接

在小學，教師是以鼓勵、誘導、啟發(fā)等教學方法，使學生樹立學習信心，進而培養(yǎng)他們學習數(shù)學的興趣。到中學階段，教師也應該注意繼續(xù)激發(fā)學生學習數(shù)學的興趣。例如，在各個學科開展豐富多彩的學科實踐活動之際，根據(jù)七年級的數(shù)學教學內(nèi)容，筆者所在學校年級組的幾位教師集體備課，設(shè)計學科實踐活動方案，利用開展學科實踐活動的契機，提升學生學習數(shù)學的興趣。其中，開展了“數(shù)學大講”，學生積極準備課件，主動搜集從古至今的數(shù)學家的素材，積極踴躍地在年級進行演講。又如，利用拔河比賽這個本來應該是體育教師設(shè)計和組織的活動，開展成為數(shù)學教師組織的一個活動。其中，從場地設(shè)計、比賽規(guī)則的制定和比賽過程的設(shè)計都由學生來完成，學生積極參加的同時，要求對比賽中運用到的數(shù)學知識進行總結(jié)歸納。例如，前期方案設(shè)計過程中，各班參賽人數(shù)的設(shè)定，需經(jīng)歷調(diào)查和統(tǒng)計的知識，運用了“數(shù)據(jù)的收集與整理”。在場地的設(shè)計中，紅領(lǐng)巾的位置的確定，運用了線段中點的確定；粉筆畫直線的過程，體現(xiàn)點動成線；測量到中間線兩邊的距離各1.5米的點，用到點到直線的距離；畫出兩條界限，運用了兩點確定一條直線，還有軸對稱和概率等知識也都運用到其中。活動結(jié)束，學生積極主動地發(fā)言，感慨萬千，在小學時他們也參加過無數(shù)次的拔河比賽，沒想到居然還可以用到許多數(shù)學知識。因此，在教學過程中，充分利用生動的事例，生活中的數(shù)學問題來培養(yǎng)學生的學習興趣，激發(fā)學生的學習熱情，運用和藹可親的笑容，幽默詼諧的語言，營造濃郁的學習氛圍，調(diào)動學生的學習積極性。

五、作業(yè)書寫格式的銜接

從初中開始，教師要對作業(yè)格式做統(tǒng)一的要求，嚴格按照要求格式認真書寫。在平時的作業(yè)評比和檢測中，可以對書寫格式賦予一定的分值，引起學生的重視，這樣經(jīng)過一段時間的訓練，學生自然就規(guī)范書寫了。

六、中小學數(shù)學教師之間的有效聯(lián)系

打破中小學數(shù)學教師之間的界限，給中小學數(shù)學教師多些交流、探討和加深了解的空間和時間。筆者所在學校是九年一貫制學校，為了達成這個目的，學校給全體中小學數(shù)學教師提供了很好的學習和交流的平臺。請市里的專家來校指導中小學數(shù)學教師做課，課題精選中小學數(shù)學教材中的“銜接點”。首先，中小學教師集體研究出體現(xiàn)中小銜接的課題，然后，分工設(shè)計教學案，經(jīng)過研討修改，經(jīng)歷試講，再修改，再正式講的過程，把每個課題都經(jīng)歷多次打磨，最后形成能體現(xiàn)中小學數(shù)學有效銜接的教學設(shè)計及優(yōu)秀課例。例如，“平方差公式”和“列一元一次方程解應用題”等課題的設(shè)計。

在北京師范大學出版社出版的《學科能力標準與教學指南：初中數(shù)學》一書中明確指出：“當前北京市初中數(shù)學教學中存在的問題——教師需要進一步加深對初中數(shù)學課程的整體認識。”筆者認為這不只是要求初中數(shù)學教師對初中數(shù)學課程的整體認識，也應該需要初中教師認識小學階段的課程和了解高中階段的課程。從而有效達成中小學數(shù)學教師學科能力的銜接，進而達成中小學數(shù)學教學的真正銜接。

總之，只有在中學的數(shù)學教學中注意以上各方面，才能使學生完成從小學到初中的順利過渡，才能使學生各方面的素質(zhì)適合初中階段學習任務，才能使學生更加輕松愉快地學好初中數(shù)學的全部課程，才能體現(xiàn)中小學數(shù)學教學的連續(xù)性和統(tǒng)一性。endprint