基于雙勢阱系統的混沌振動研究

劉樹勇， 位秀雷， 王 基， 俞 翔

(海軍工程大學 動力工程學院，武漢 430033)

混沌振動是混沌科學研究的重要課題，國內外學者圍繞混沌振動的應用、控制和識別等問題開展了廣泛的研究[1]。為了應用有益混沌振動，Yu等[2-3]提出廣義混沌同步技術消減了船舶輻射噪聲線譜，提高了其隱身性能；龍運佳等[4]研究了混沌振動壓路機的應用，提高了壓實效果。為了控制有害的混沌振動，韓建群等[5]應用滑模控制方法隔離了設備中的Lorenz混沌振動，消除了破壞儀器設備混沌運動；高遠等[6]應用自適應跟蹤控制方法，抑制了汽車懸架的大幅值混沌振動，有效降低了懸架垂向振動加速度；熊懷等[7]研究了非線性能量阱(Nonlinear Energy Sink, NES)對振動的抑制方法，得到了阻尼對NES的影響規律。目前，在混沌振動的研究方法上，數值仿真研究和試驗研究仍然是兩種主要手段[8]。陳立群等[9]通過仿真研究了混沌振動的開閉環控制技術；韓保紅等[10-11]應用數值方法研究了混沌振動的主動隔振問題；梁山等[12]對兩自由度汽車懸架模型的非線性混沌振動進行了仿真與實驗研究，揭示了該系統存在混沌的可能性。

事實上，由于混沌振動問題的復雜性[13]，導致混沌試驗研究具有一定的困難，目前大部分研究工作還局限在理論分析和計算層面，缺乏試驗的驗證，特別是要產生穩定的、可重復出現的混沌是一件非常困難的工作。然而，要將混沌應用于工程實際，必須開展深入的試驗研究，掌握混沌產生的實際條件、混沌出現的規律以及不同參數對混沌的影響，在這方面，國內外學者都進行了嘗試。任成龍等[14]為了模擬路面的復雜激勵，應用多連桿機構設計了懸架振動臺，取得了較好的實驗結果。Moon[15]開展了懸臂梁的混沌振動試驗研究，主要探討了兩種情況下系統的響應：一是梁的振動幅值處于較小的范圍內，可以簡化為線性方程，但其自由端受非線性力或邊界條件有非線性特性；二是梁振動幅值非常大，本身有明顯的幾何非線性。在這些條件下，系統可能產生混沌振動。雖然這些研究工作為混沌試驗提供了思路，但具體還存在如下問題需要解決：①如何在系統中產生持續穩定的混沌運動；②如何準確確定實際系統的混沌參數區域；③如何對復雜條件下的混沌信號進行有效分析；④如何在工程實際中實現小振幅的混沌運動。本文利用Moon提出的雙勢阱系統設計了單端磁吸式混沌振動試驗裝置，并開展了深入的理論和試驗研究，通過對實測數據進行分析，結果表明，該裝置切實可以產生穩定的、可重復實現的混沌振動，從而為后續混沌應用研究奠定了堅實的基礎。

1 雙勢阱系統的非線性特征

由磁鐵和懸臂梁構成的雙勢阱系統動力學方程可以簡化為

(1)

式中：ξ為系統無量綱阻尼參數；γ為無量綱線性剛度；β為無量綱非線性剛度；f無量綱激勵力幅值。對于式(1)，其彈簧作用力為：F(z)=-γz-βz3定義其勢函數V(z)為V(z)=γz2/2+βz4/4。當參數的取值為γ=-1，β=1時，雙勢阱如圖1所示。

因此，質點可以在雙勢阱M和N之間以及在單勢阱M或N內運動。運動形式一般分為以下幾種情況：質點在雙勢阱M和N之間周期振蕩，物理系統呈現大幅值的周期振動，如圖1(a)所示；質點在單勢阱M和N內運動，物理系統呈現出小幅值的周期振動，如圖1(b)和圖1(c)所示；質點在雙勢阱M和N之間無規律來回振蕩，具體表現為在單邊勢阱M和N內運動后，越過勢阱壁壘進入到另一個勢阱中，但在勢阱中運動時間不同，是非周期振動模式，如圖1(d)所示。但由于它是在確定性系統中產生的類隨機行為，因而具有混沌性質。

圖1 雙勢阱示意圖Fig.1 Two potential well sketch map

(2)

(3)

(4)

假設系統的響應中包含了快變和慢變分量，具有多時間尺度特征，分別設為T0=t，T1=εt，因此式(4)可以寫為

(5)

式(5)的解可以展開成

z(T0,T1)≈z0(T0,T1)+εz1(T0,T1)

(6)

將式(6)代入式(5)得到

(7)

令等式兩邊小參量ε的系數為零得到

(8a)

pz0(T0,T1)+αz0(T0,T1)3+ω2z1(T0,T1)+

(8b)

令基本解幅值和相位為時變參數

z0(T0,T1)=B(T1)cos(T0+φ(T1))

(9)

聯立式8(b) 和式(9)得到

(10)

將式(10)等式右邊項應用三角函數關系展開，并消除共振項，即令cos(T0+φ(T1))和sin(T0+φ(T1))的系數等于零得到

δB(T1)+2B′(T1)=0

(11a)

(11b)

因此可以求出

(12a)

(12b)

(13)

式中，φ0為積分常數。聯立式(10)和式12(a)得到

(14)

因此，可以由式(14)解出z1(T0,T1)為

z1(T0,T1)=-αB(T1)3cos(3T0+φ(T1))/4(ω2-9)

(15)

因此求得系統的解為

(16)

以T0=t，T1=εt替換后得到

(17)

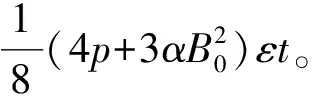
應用平均法[18]推導了式(5)的幅值和頻率之間的關系

16γ2[p2ε2+δ2ε2+2pε(ω-1)2+(ω-1)4]}=0

(18)

式中，參數γ為平均法計算過程中所采用的極坐標幅值，其本質含義為Van der Pol平面上振動幅值的大小。當ε=1,α=1,ω=1,A=6,δ=0.5,δ=1.0,δ=1.5時，改變調節因子p的大小，得到p-γ曲線如圖2所示。從圖中可以觀察到系統的非線性“舌狀”結構特征。

圖2 系統的幅值特征曲線Fig.2 Amplitude frequency characteristic curve

2 試驗臺架結構設計

為了驗證系統的非線性以及可能具有的混沌特征，開展了試驗研究。根據混沌產生的必要條件，在混沌振動試驗裝置設計過程中，需要選擇合適的非線性元件作為試驗臺的組成部分，主要利用系統結構非線性、材料非線性或者電路的非線性等產生混沌；其次確保系統中沒有隨機信號輸入，從而實現由確定性系統產生類似隨機的不確定性行為；在此基礎上，編制混沌識別程序對系統的動力學行為進行識別，通過定性分析技術對采集的時間歷程圖進行目視觀察，同時利用相空間重構原理，觀察實測時間序列相平面圖、Poincaré截面圖；利用定量分析方法提取信號的特征，進行Fourier分析得到信號的頻譜特征；計算信號的分形維數和Lyapunov指數；調節系統參數，觀察到系統由不同周期態進入混沌態的途徑。

基于以上考慮，雙勢阱單端磁吸式混沌振動裝置如圖3所示。裝置由如下部分組成：激振器、支座、薄彈片、磁鐵、小鐵片、外部固定框架、固定彈片裝置。各部件的具體功能為：①激振器，提供穩定外部激勵，保持整個系統持續穩定振動；②支座，固定激振器，為了保證裝置在水平方向上不受其他外力影響，需嚴格保持激振器水平放置；③薄彈性片，為整個裝置的主體元件，為保證薄片具有良好的恢復力，剛度不易太硬，并且薄片的寬度不宜太小，這樣可以減少薄片做水平擺動之外的運動；④磁鐵(方形磁鐵)， 提供彈片端部吸引力，固定磁鐵的支座可以左右水平移動，進而調節磁力作用距離；⑤質量塊，安裝在薄彈片自由端，受到磁力作用，它和磁鐵一起形成了裝置的雙勢阱，為保證薄彈片不產生水平擺動之外的運動，其質量不宜過大；⑥外部固定框架，框架需滿足兩個要求，不能是磁性材料，以免對彈片運動形成外部干擾；質量不宜過大，否則難以保持整個框架的水平性，從而彈片的水平擺動會受到外部力的干擾；⑦彈片固定裝置，在兩個夾緊螺母和彈片之間設置一個方形鐵片，將螺母和彈性片之間的點接觸擴展成面接觸，從而使彈片固定更牢靠；⑧設計實驗參數，激光位移傳感器，型號CD33-30NV，測試最大位移為±4 mm，最大允許誤差為±0.1%F.S.；激光位移傳感器與梁的距離為30 mm；梁的長與寬尺寸為155 mm×20 mm；磁鐵尺寸長寬高為11 mm×6 mm×9 mm；磁鐵頂端到底面高度為24 mm；質量塊重量為5 g。

圖3 雙勢阱單端磁吸式混沌振動裝置Fig.3 Sketch of the experimental rig

3 試驗步驟

實驗本質為正弦信號的慢速頻率掃描實驗，掃描頻率范圍為5～25 Hz，采樣頻率為2 kHz，數據采集時長為5 s。具體實驗步驟為：

步驟1 安裝實驗裝置，設置磁鐵距中心線的距離、無激勵時薄彈片距底端的距離，布置位移傳感器；

步驟2 將功率放大器置于高阻位置，設置最大電流限制值，并通過調節增益來實現激勵力大小的改變；

步驟3 打開數據采集系統以及信號發生系統，打開LabVIEW軟件，建立采集信號的時間歷程窗口、功率譜窗口及相圖以作實時觀察；

步驟4 固定激勵頻率于特定值，調節功率放大器增益旋鈕，觀察信號的時間歷程圖與功率譜圖，待其穩定后采集數據以備后處理之用，數據文件按H××L××S×××.lvm命名，H后為激勵幅值，L后為磁鐵距中心線的距離值，S后為無激勵時薄彈片距底端的距離值，在文件名中以p標識小數點；

步驟5 以步長為0.1 Hz增加頻率，重復步驟4，直至完成一定范圍的頻率掃描；

步驟6 改變磁鐵距中心線的距離、無激勵時薄彈片距底端的距離，重復步驟3～步驟5；

步驟7 信號分析流程，對信號時域圖進行目視觀察、提取和分析實測數據的頻率特征、計算相空間重構參數、重構原系統的吸引子、計算吸引子的特征指數；

步驟8 根據分析結果，給出系統的可能的混沌參數區域；

步驟9 提出改進試驗方案和進一步研究內容。

4 試驗結果

4.1 系統響應隨激振系統增益變化的結果

根據掃頻調試，發現當激勵頻率大于10 Hz時，系統的響應呈現豐富的動力學特征，因此，本試驗中將重點研究的頻率范圍設置在10 ～25 Hz。同時，考慮到功率放大器的增益過大時，將對試驗裝置產生破壞性作用，因此增益的范圍確定為0～1.5 V。

當激勵頻率為15.6 Hz，激振系統功率放大器的增益為0.1時，系統在右勢阱中處于周期1狀態，時間歷程曲線如圖4所示，振動的最大幅值為0.056 mm，從頻譜圖中可以觀察到系統出現了基頻和三倍頻46.8 Hz，系統的重構吸引子為一個極限環，從而證實了近似解析解分析的正確性。在這種狀態下，用力杠加入小的外部擾動，系統在兩個磁鐵之間振蕩，隨后落入左勢阱并進入周期1運行狀態，這表明外部激勵力不足以使其越過勢阱壁壘，因而被限制在單邊勢阱內。

當激勵頻率為15.6 Hz，激振系統的增益為0.5時，系統的振動幅值增大，達到0.172 1 mm，但仍然處于周期1運動狀態，如圖5所示。從時域圖和頻域圖中，可以觀察到系統的規則運動以及明顯的線譜特征。重構了系統的吸引子，它是一個極限環。應用改進的Poincaré截面法對系統的響應進行了分析，得到了截面圖。注意實測數據Poincaré截面圖和傳統的仿真數據不同，它是一個點簇而不是單個點，因此在編程過程中，需要將距離近的截點歸屬到同一點，這樣才能反映系統的本質特性，這和仿真研究有明顯的差異，如圖5(d)所示。

圖4 激振系統增益為0.1 V時系統的振動響應Fig.4 The vibration response when the excitation gain is 0.1 V

圖5 激振系統增益為0.5 V時系統的振動響應Fig.5 The vibration response when the excitation gain is 0.5 V

繼續增大增益為0.8時，系統的振動幅值進一步增加，但此時的狀態是一種臨界狀態。用力杠加入小的擾動后，系統進入混沌狀態。系統在左右勢阱之間以混沌模式振蕩。有趣的是，系統隨后又落入左單邊勢阱并處于周期1振動，這是一種不穩定混沌現象。而增益參數為0.95時，系統出現1/2次諧波，頻率為7.83 Hz，表明此時系統出現了倍周期分岔行為，如圖6所示。

圖6 激振系統增益為0.8 V時系統的振動響應Fig.6 The vibration response when the excitation gain is 0.8 V

在增益為0.98時，無需力杠擾動，系統自動進入穩定的混沌運動狀態。時間歷程圖如圖7(a)所示，具有明顯的貌似隨機特征，功率譜呈現寬譜。重構相空間參數中嵌入維數為4，延遲時間為16。得到的重構混沌吸引子如圖7(e)所示，計算得到的最大LE為0.031 3，關聯維數為2.129。

圖7 激振系統增益為0.98 V時系統的振動響應Fig.7 The vibration response when the excitation gain is 0.98 V

4.2 系統響應隨激振頻率變化的結果

由前面的試驗可總結出兩個規律：①激振系統的增益為0.5時，不容易進入混沌狀態，而是在單邊勢阱內處于周期1運動；②激振系統增益大于0.95時，系統的動力學行為非常豐富，可以產生包括混沌在內的不同振動模式。為了證實該結論，在增益為0.5的條件下，改變激勵頻率從10～20 Hz，系統的響應都為周期1模式。結果發現，在頻率為15～17 Hz，加入小的外部擾動，系統能產生暫態混沌行為，隨后落入勢阱內，處于周期1狀態。

為了觀察系統的混沌響應并進一步證實以上規律的準確性，將激振系統的增益固定為1，由小到大增加系統的激勵頻率。當頻率為5～10 Hz時，系統處于周期1狀態；當激勵頻率大于10 Hz時，系統的響應特征非常豐富：在10～16 Hz時，產生混沌振動；在16.6 Hz時，系統出現周期2行為，如圖8所示，計算其LE為-0.008 5。在17～19 Hz時，又產生并保持穩定的混沌運動，如圖9所示。而在高頻時，系統出現了逆分岔行為，由混沌自動進入周期運動，19 Hz時，產生周期3運動，如圖10所示；在19.4 Hz時，產生單勢阱內的多周期運動，如圖11所示。此外，還觀察到了一些有趣的現象，在23 Hz時，質量塊穿越勢阱壁壘在兩個勢阱之間來回運動，產生了大幅值的多周期振動；在30 Hz激勵時，裝置出現轟鳴聲，系統可能出現了共振現象。越過共振頻率后，振子在單邊勢阱內呈周期1運動模式。

圖8 系統產生的周期2振動Fig.8 Periodic 2 motion of the system

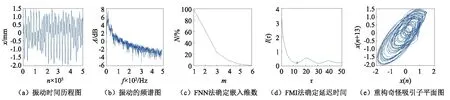
圖9 系統產生的混沌振動Fig.9 Chaotic motion of the system

圖10 激勵頻率為19 Hz系統產生的周期3振動Fig.10 Periodic 3 motion of the system

圖11 激勵頻率為19.4 Hz時系統產生的多周期振動Fig.11 Multi periodic motion of the system

5 結 論

應用多尺度法可以有效求出雙勢阱系統自由振動響應的近似解析解，從響應表達式中可知系統動力學行為中存在慢變分量和快變分量，并存在超諧波響應。采用平均法得到了系統的幅頻關系表達式，給出了振動幅值和頻率調節因子之間的舌狀結構曲線，揭示了系統的非線性本質特征。成功設計并加工了雙勢阱理論的機械式混沌振動試驗裝置，其意義在于進一步證實了機械系統中不僅能夠產生可以復現的、穩定的混沌振動，而且可以通過試驗獲得混沌參數區域，為混沌的工程應用研究提供了可靠的試驗手段。

通過實測數據的分析，觀察到了試驗中的次諧波現象，它的出現的預示著混沌產生；觀察到了超諧波現象和混沌現象，同時觀察到了一些有趣的新現象：如系統周期1運動存在兩種模式，一種是在兩個勢阱之間周期振蕩，另一種是陷入某一個勢阱內做周期1運動，試驗研究證實了理論分析的有效性。后續研究中，還需要完成一些工作：如彈片的長度變化與剛度變化對混沌的影響、附加質量的改變、多頻激勵、多自由度等因素對系統的影響、多勢阱系統的三維混沌振動、設計能夠精確控制初始條件的結構以及驗證本項目組編制的混沌在線識別系統。

致謝：

楊慶超講師和Southampton University Solent Institution of Acoustic: Jian Jiang, Chris, Lee, Lawrance的討論。

[ 1 ] ZAMBRANO S，SABUCO J， SANJUAN M A F. How to minimize the control frequency to sustain transient chaos using partial control[J]. Communications in Nonlinear Science and Numerical Simulation，2014，19(3)： 726-737.

[ 2 ] YU Xiang， ZHU Shijian， LIU Shuyong. A new method for line spectra reduction similar to generalized synchronization of chaos[J]. Journal of Sound and Vibration，2007， 306(3/4/5)：835-848.

[ 3 ] 俞翔, 朱石堅, 樓京俊. 基于碰撞振動的隔振系統混沌化實驗研究[J]. 振動與沖擊, 2014, 33(18): 59-64.

YU Xiang, ZHU Shijian, LOU Jingjun. Tests for chaotification method of a vibration isolation system with a vibro-impact subsystem [J].Journal of Vibration and Shock, 2014, 33(18): 59-64.

[ 4 ] 龍運佳，楊勇，王聰玲. 基于混沌振動力學的壓路機工程[J]. 中國工程科學，2000，2(9)： 76-79.

LONG Yunjia， YANG Yong， WANG Congling. Road roller engineering based on chaotic vibration mechanics[J]. Engineering Science， 2000， 2(9)： 76-79.

[ 5 ] 韓建群，鄭萍.一種簡單的Lorenz混沌振動主動隔振方法[J].系統工程與電子技術，2006，128(10)： 1566-1568.

HAN Jianqun，ZHENG Ping. Active control isolation for the Lorenz chaotic vibration with a simple method[J]. Systems Engineering and Electronics， 2006， 128(10)： 1566-1568.

[ 6 ] 高遠，耿兆云，范健文. 汽車懸架系統中混沌振動的自適應跟蹤控制研究[J]. 機械設計與制造, 2013(12)： 198-201.

GAO Yuan，GENG Zhaoyun，FAN Jianwen. Control chaos in automobile suspension system via adaptive tracking control method[J]. Machinery Design & Manufacture， 2013(12)： 198-201.

[ 7 ] 熊懷,孔憲仁,劉源.阻尼對耦合非線性能量阱系統影響研究[J]. 振動與沖擊, 2015, 34(11): 116-121.

XIONG Huai, KONG Xianren, LIU Yuan. Influence of structural damping on a system with nonlinear energy sinks[J]. Journal of Vibration and Shock, 2015, 34(11): 116-121.

[ 8 ] WIERCIGROCH M， SIN V W T, LI K. Measurement of chaotic vibration in a symmetrically piecewise linear oscillator[J]. Chaos Solitons & Fractals， 1998， 9(1)： 209-220.

[ 9 ] 陳立群，劉延柱. 混沌振動系統的開閉環控制[J]. 應用科學學報，1999， 17(4)： 445-449.

CHEN Liqun， LIU Yanzhu. The open-plus-closed-loop control for chaotic oscillations[J]. Journal of Applied Sciences， 1999， 17(4)： 445-449.

[10] 韓保紅，馬英忱，閆石. 用Matlab仿真非線性混沌振動的主動隔振研究[J]. 控制與決策， 2003， 18(1)： 120-122.

HAN Baohong，MA Yingchen，YAN Shi. Active control isolation research for a class of nonlinear chaotic vibration systems[J]. Control and Decision， 2003， 18(1)： 120-122.

[11] 韓保紅，閆石，焦耀斌，等.一類非線性混沌振動的主動隔振實驗研究[J]. 噪聲與振動控制，2002， 22(2)： 24-28.

HAN Baohong，YAN Shi，JIAO Yaobin，et al. Active control isolation research for a class of nonlinear chaotic vibration systems[J]. Noise and Vibration Control， 2002， 22(2)：24-28.

[12] 梁山，鄭劍，朱勤，等. 非線性車輛模型混沌振動的仿真與實驗研究[J]. 機械強度，2012， 34(1)： 6-12.

LIANG Shan，ZHENG Jian，ZHU Qin，et al. Numerical and experimental investigations on chaotic vibration of a nonlinear vehicle model over road excitation[J]. Journal of Mechanical Strength， 2012， 34(1)： 6-12.

[13] YOSHIDA K，SATO K, YAMAMOTO S，et al. Charac-terization of chaotic vibration without system equations[J]. International Journal of Non-linear Mechanics， 1997， 32(3)： 547-562.

[14] 任成龍，葛翔. 懸架混沌振動臺的設計[J].南京工程學院學報(自然科學版)， 2009， 7(4)： 37-42.

REN Chenglong，GE Xiang. Design of suspension chaotic vibration table[J]. Journal of Nanjing Institute of Technology(Natural Science)， 2009， 7(4)： 37-42.

[15] MOON F C. Chaotic vibrations： an introduction for applied scientists and engineers[M]. New York： Wiley， 1987.

[16] YAN Yan, WANG Wenquan, ZHANG Lixiang. Applied multiscale method to analysis of nonlinear vibration for double-walled carbon nanotubes[J]. Applied Mathematical Modelling, 2011, 35(5): 2279-2289.

[17] MITCHELL L, GOTTWALD G A. On finite-size Lyapunov exponents in multiscale systems[J]. Chaos, 2012, 22(2): 1-26.

[18] OKABE T, KONDOU T, OHNISHI J. Elliptic averaging methods using the sum of Jacobian elliptic delta and zeta functions as the generating solution[J]. International Journal of Non-Linear Mechanics, 2011, 46(1): 159-169.