考慮遲滯效應的圓柱體渦激振動分析研究

康 莊， 張立健， 倪問池

(哈爾濱工程大學 深海工程技術中心， 哈爾濱 150001)

在深海工程領域，圓柱體結構例如海洋立管是工程上應用最多最廣泛的一種結構物，當水流繞過圓柱體時，會發生結構物后漩渦脫落的現象，交替的漩渦會激發與來流方向垂直的流體作用力，致使結構物產生振動，當泄渦頻率與固有頻率接近時，將會發生“共振”現象，同時圓柱振動幅值將增大[1]。圓柱體渦激振動(Vortex-Induced Vibration, VIV)一直都是研究所關注的熱點問題。國內外眾多學者進行了彈性支撐圓柱渦激振動研究。黃維平等[2-4]基于流固耦合的渦激升力模型和Morison方程，提出了一個非線性的圓柱體渦激振動時域分析模型，并且采用ANSYS-CFX 軟件對細長柔性圓柱體雙自由度渦激振動進行了深入研究。Jauvtis等[5]通過實驗發現，當質量比為7時，單自由度與雙自由度渦激振動試驗結果類似，其橫向最大振幅為1.05D附近，當質量比為2.6時，雙自由度橫向振幅出現“超上端分支”，其幅值達到1.5D，彈性支撐雙自由度渦激振動出現如此大橫向振幅，此現象是以前從未發現的。谷家揚等[6]希望采用數值模擬方法研究“超上端分支”現象，然而即使將無因次阻尼比ξ設為0，模擬出的最大橫向振幅也不超過1D。部分學者注意到, 試驗結果或者計算結果跟初始條件有很大的關系，Guilmineau等[7]參照Jauvtis等的單自由度低質量比試驗，計算了2D橫向彈性支撐圓柱(m*=2.4,m*ξ=0.013)的渦激振動,數值模擬采用了三種初始條件:①速度保持均勻不變;②速度由最高逐漸減小;③速度由最低逐漸增加。計算結果表明：圓柱橫向振幅與初始條件有關:僅在①和②條件下預測到了“下支”響應;在條件③時,觀察到了“上支”。試驗采用了勻加速和勻減速的形式，從而產生了“遲滯現象”，而數值模擬一般采用固定速度形式，遲滯現象對渦激振動響應有顯著影響。

CFD(Computational Fluid Dynamics)模擬采用固定速度初始條件時，會忽略尾流模態的“慣性”對流場影響[8]。最近，Kim等[9-12]采用數值模擬方法對圓柱渦激振動開展研究，更深入闡述渦激振動的機理。本文在前人的基礎上利用開源軟件OpenFOAM采用勻加速，勻減速和勻速三種初始條件對質量比為2.6雙自由圓柱渦激振動模擬。研究考慮遲滯效應與不考慮遲滯時，圓柱振動幅值，鎖定區間，升力系數，阻力系數以及尾渦的變化。同時針對遲滯機理進行討論，并研究了加速度的大小對遲滯現象的影響。

1 計算模型與模擬工況

1.1 計算模型建立

本文基于OpenFoam嵌入自編程序進行圓柱渦激振動數值模擬，計算域描述如圖1所示。

圖1 計算域幾何示意圖Fig.1 Digram of computational domain

計算區域為左邊及上下邊距圓心6D，右邊距離圓心20D的矩形流域，采用URANS二維模型，在z向設置為“empty”邊界條件。網格劃分必須確保“低雷諾數”處內的網格質量，“低雷諾數”并不是指整體雷諾數較低，而是指黏性子層處的雷諾數較低，為了描述黏性子層內的流動引入無量綱數y+，y+與壁面剪切應力有關。y+的計算公式由式(1)得出

(1)

式中:τw為壁面剪切力。

網格劃分必須確保第一層網格厚度能使得y+<1。為了保證圓柱面處網格的厚度同時保證整體網格不過多導致計算時間冗長，因此在網格劃分時，需要將圓柱周圍局部加密，將計算域劃分為9個區域，圓柱周圍4D的范圍內采用O型網格。遠場區域采用結構網格，其尺寸逐步遞增，如圖2 所示。

采用SST(Shear Stress Transport)k-ω湍流模型和非穩態一階隱式進行求解，動量方程的壓力速度耦合采用PIMPLE算法，動量、湍流動能、耗散率項均采用二階迎風格式。

(a) (b)圖2 網格計算區域劃分示意圖Fig.2 Grid computing region division

1.2 時間步長控制以及網格無關性

時間步長影響著收斂速度和穩定性。合理的調整時間尺度，能夠在獲得理想收斂速度和穩定性的同時縮短計算時間。庫朗數(Courant Number)指的是時間步長和物理空間尺度的對應關系，對于湍流而言有著重要影響，庫朗數由式(2)表示

Cn=u·Δt/Δx

(2)

式中:Cn為庫朗數;u為來流速度;Δt為時間步長;Δx為網格尺寸。為滿足Courant-Friedrichs-Lewy條件,必須要求庫朗數足夠小。使用數值模擬計算時候，設定庫朗數最大值小于0.50，時間步長取為Δt=0.000 1。

通過Re=104的圓柱繞流為例驗證網格無關性，采用第一層網格厚度為0.02 mm，近壁面第一層網格的長厚比設置為8∶1。根據網格加密與放疏原則，設置了不同的五種網格方案，不同網格方案的詳細參數如表1所示。

表1 不同網格設計方案

將阻力與斯特勞哈爾數的結果隨網格總體數量的關系繪制在圖3和圖4中，由圖3和圖4可知，當網格數達到以及超過51 502時，計算的阻力系數與斯特勞哈爾數均達到了比較好的收斂。而網格數低于51 502時，阻力與斯特勞哈爾數偏差較大，由圖3可以知：網格3已經能夠滿足計算精度的需求。

圖3 阻力均值隨網格數量變化趨勢Fig.3 The mean drag coefficient with different grid

圖4 斯特勞哈爾數隨網格數量變化趨勢Fig.4 The mean drag coefficient with different grid

1.3 模擬工況

選取Javutis等(2004)所做的經典的m*=2.6的雙自由度實驗作為參考，圓柱直徑為0.038 1 m，質量阻力比m*ξ=0.13，固有頻率為0.4 Hz，流向與橫向頻率比fnx/fny=1,約化速度范圍為2～14，約化速度間隔為0.2。

本文對速度的控制是在OpenFOAM的速度自定義函數中實現的，在數值模擬過程中，三種約化速度的實現方式如下定義：

(1)勻加速。約化速度從2逐步增加，加速度為每無量綱單元時間(Ut/D)約化速度增加0.025，增加至目標速度后保持該約化速速繼續模擬30個周期，同時上一個折合流速模擬結束時刻的物理場是下一個折合流速模擬的初始條件。

(2)勻減速。約化速度從14逐步減少，加速度為每無量綱單元時間(Ut/D)約化速度減小0.025，減小至目標速度后保持該約化速速繼續模擬30個周期，同時上一個折合流速模擬結束時刻的物理場是下一個折合流速模擬的初始條件。

(3)勻速。在數值模擬開始時，約化速度直接給定為目標約化速度，隨后保持該約化速度繼續模擬。

本文對速度的控制是在OpenFOAM的速度自定義函數中實現的，三種初始條件下圓柱渦激振動各工況參數如表2所示。

表2 三種初始條件下數值模擬工況

2 計算結果與分析

2.1 渦激振動幅值響應

圖3給出了不同初始條件下雙自由度圓柱渦激振動橫向振幅隨約化速度變化曲線，方塊代表Jauvtis等的試驗結果，圓點代表采用勻加速方法，正三角代表采用勻減速方法，倒三角代表采用勻速方法。由圖5可知，三種方式均捕獲到初始分支和下端分支，采用勻加速方式時，在Ur(約化速度)=6.8時，Ay/D達到最大值1.4D。在Jauvtis等的m*=2.6試驗中，Jauvtis等發現在約化速度為8.3，橫向達到最大振幅比1.5D，他定義該分支為“超長端分支”，因此可知勻加速數值模擬可以捕獲到“超上端分支”現象，但是其值較為提前并且結果略小。當Ur>6.8時，振幅下降至0.75D步入下端分支。采用勻減速方式時，捕獲到上端分支，上端分支與下端分支交界點為Ur=6時，其最大橫向振幅為0.96D，當約化速度大于6時，振幅比Ay/D陡然下降到0.7D附近，進入“下端分支”。采用固定速度方式時，沒有捕獲到上端分支，初始分支與下端分支交界點為Ur=5，其最大振幅0.85D。在下端分支中，勻加速的振幅略大于試驗而勻減速和勻速的振幅略小于實驗值。采用勻加速與勻減速初始條件可以數值模擬出遲滯現象，如圖5中箭頭所示。然而值得注意的是，Jauvits等(2004)試驗的遲滯區域為7.8～8.6，而數值模擬得到的遲滯區域為6～6.8。數值模擬的遲滯區域相對于試驗提前了2左右，但是遲滯區域的范圍大致都為0.8個約化速度。

圖5 不同初始條件下圓柱橫向最大振幅Fig.5 Transverse max amplitude in different initial conditions

圖6給出了不同初始條件下圓柱渦激振動流向振幅隨約化速度變化曲線。由圖6可知，采用勻加速方式時，在Ur=6.8時，Ax/D達到最大值0.29D。Jauvtis等的試驗中在約化速度為7.3時達到中最大流向振幅比為0.32D，數值模擬結果較為提前并且結果偏小。當Ur>6.8時，振幅下降至0.07D步入下端分支。采用勻減速方式時，在Ur=6時，Ax/D達到最大值0.11D，數值模擬得到的遲滯區域為6～6.8。

對比圖5與圖6可知，當Ur≤4時，渦激振動處于初始分支中，圓柱體兩側漩渦對稱地脫落，產生的升力互相抵消一部分，此時橫流向運動雜亂且運動幅值較小，而順流向運動規則且幅值較大，軌跡呈扁平狀。在初始分支內，三種速度方式的流向振幅均保持較高的振動幅值。當Ur>4時，渦激振動進入鎖定區域，圓柱形圓柱體兩側漩渦開始交替脫落，此時，橫向作用力使橫向運動幅值變大，同時順流向運動幅值也增大。進入鎖定區后，采用勻加速與勻減速的流向振幅隨Ur的增大而逐步增大至極值。采用勻速初始條件時，由于流向振幅進入鎖定區后沒有捕獲到上端分支，因此流向振幅表現為“雙峰”現象，在初始分支Ur=3時達到極值0.14D，在Ur=8時達到次峰0.075D。

圖6 不同初始條件下圓柱渦激流向振幅Fig.6 In-line max amplitude in different initial conditions

2.2 無因次約化振動頻率響應

圖7給出了圓柱渦激振動橫向約化頻率隨約化速度變化曲線，在圖中添加兩條輔助線，實線為運動頻率等于自振動頻率輔助線，虛線為固定圓柱卸渦頻率預估線。由圖7可知，采用勻加速條件時：圓柱無無因次鎖定頻率在1.3附近。采用勻減速和勻速條件的鎖定頻率在1.25附近，數值模擬的鎖定頻率均小于實驗值的1.35。三種初始條件下的鎖定區域有很大的不同。采用勻加速條件時，渦激振動鎖定區范圍為4.2～12.8，其中處于上端分支的為4.2～6.8，處于下端分支的為6.8～12.8；當采用勻減速條件時，渦激振動鎖定區范圍也為4.2～12.8，但處于上端分支的為4.2～6，處于下端分支的為6～12.8；采用勻速條件時，渦激振動鎖定范圍為3.8～14，其中處于上端分支的為3.8～5，處于下端分支的為5～14。在鎖定區間內圓柱保持高幅值振動，在鎖定區外，振動頻率離開實線向虛線靠攏，表現為固定圓柱泄渦頻率。采用勻加速與勻減速可以得到鎖定區遲滯區為6～6.8，如圖7中箭頭所示，其相對于試驗遲滯區7.8～8.6提前約2個約化速度。

圖7 不同初始條件下圓柱橫向振動約化頻率對比圖Fig.7 Transverse reduced frequency in three initial conditions

采用勻加速初始條件時，圓柱振動頻率功率函數密度分布如圖8所示，當Ur=3時，橫向振動頻率等于固有圓柱泄渦頻率，流向振動具有兩個主要頻率，較大振動頻率對應于兩倍橫向振動頻率，較小頻率對應單倍橫向頻率，觀察不同約化速度下振動頻率可知，當約化速度較低時(Ur≤4.2)，流向振動出現了兩個主要頻率，分別為單倍與雙倍橫向頻率。當約化速度Ur=6時，圓柱振動處于鎖定區內，圓柱橫向振動頻率集中在一個頻率上即圓柱固有頻率，值得注意的是，在鎖定區域內，發現在除了主頻外，還存在一個3倍的低頻分量。Jauvtis等(2004)認為，這是由于超上端分支產生的“2T”泄渦模型從而導致產生三階升力分量。流向振動頻率為橫向頻率2倍，同時流向頻率還存在一個2倍的低頻分量。當Ur增大到12.6時，圓柱處于鎖定區向解鎖區跳躍的過渡區，圓柱橫向振動有兩個主要頻率，前一個頻率對應固有頻率，后一頻率對應于固定圓柱泄渦頻率。流向主要頻率為橫向頻率的2倍，同時出現1.5倍和2倍的低頻分量。

在鎖定區域內，橫向振動除了主頻外，還存在一個3倍的低頻分量，說明在鎖定區域內升力存在3倍低頻分量，圖9給出了Ur=6時渦激升力功率譜密度曲線。由圖9可知：采用勻加速條件下，鎖定區域內渦激升力除主頻外，還存在3倍低頻以及微弱5倍低頻。在鎖定區域內，橫向振動受3倍低頻升力影響從而產生3倍振動分量。

(a)Ur=3 (b)Ur=6 (c)Ur=12.6圖8 各約化速度下橫向振動功率譜密度曲線Fig.8 Transverse vibration frequency PSD in different initial conditions

圖9 Ur=6時渦激升力功率譜密度曲線Fig.9 Lifting force frequency PSD in increase initial conditions

鎖定區域升力3倍低頻分量可由泄渦模式所解釋，在鎖定區域內泄渦模型為“2T”模式，如圖8所示。每個“T”為一個正負交替的三重渦，一個“T”模式可以看為一對半的“2S”泄渦，如圖10圓圈中為一對“2S”泄渦，認為“2T”泄渦模式產生了升力中的3倍低頻。

圖10 “T”模式類似于一對半的“2S”模式Fig.10 “T” mode is similar to one and a half of the “2S” mode

2.3 流體力特性響應

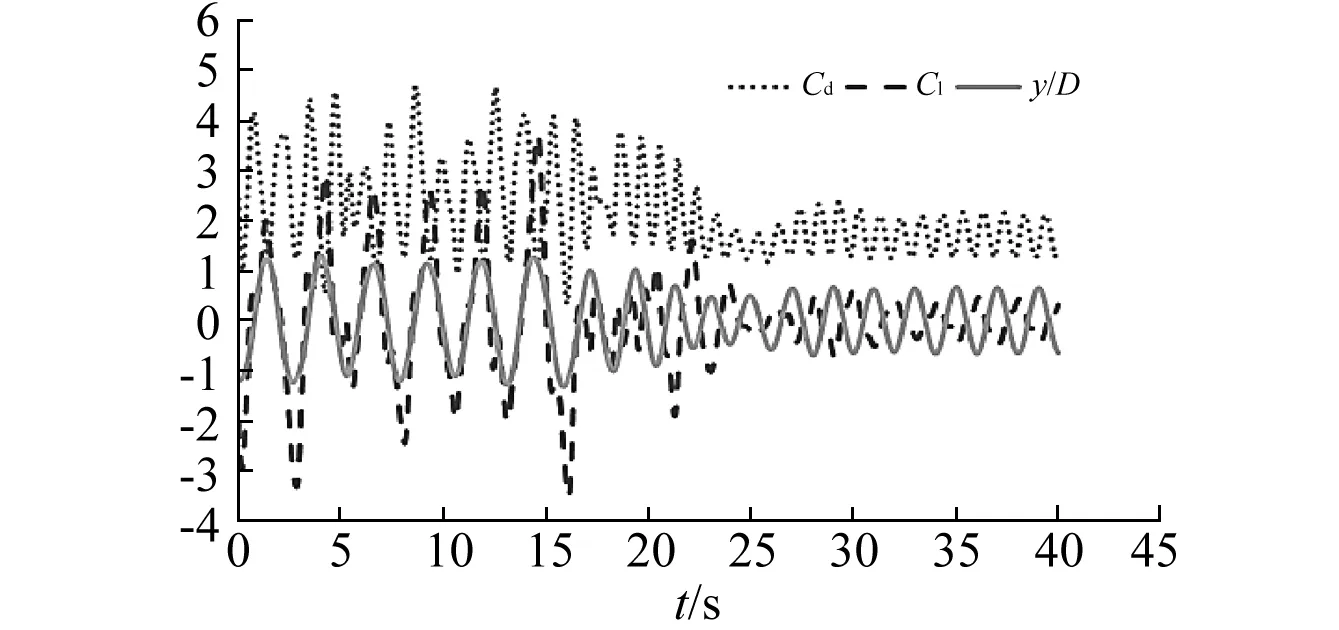
勻加速，勻減速以及勻速三種不同速度形式所得到的升力均方根和阻力均值隨約化速度變化規律如圖11所示，對于升力系數而言，采用勻加速方式時，在2

圖11 三種速度形式下升力均方根與阻力均值隨約化速度變化圖Fig.11 The RMS lift and mean drag coefficients versus Ur in different initial conditions

對比三種初始條件下的升力系數與阻力系數結果可知，作用在圓柱表面的水動力系數也存在與圓柱振幅響應相類似的遲滯區域，其區間范圍為6≤Ur≤6.8。在遲滯區間內，采用勻加速條件的升力系數較大，其對應的橫向振幅也較大。反之，采用勻減速條件的升力系數較小，其對應的橫向振幅也較小。

圖12給出了采用勻加速初始條件時無量綱位移y/D升力系數Cl以及阻力系數Cd隨時間變化曲線，當Ur=3時，此時位于“初始分支”，升力系數與阻力系數以及橫向位移均表現為規則的簡弦形式，升力曲線與位移曲線的波峰波谷處在相同位置，表現為典型的同相位角形式。當Ur=4時，圓柱上的升力以及阻力系數以及橫向位移曲線出現了“拍”現象，此區域為初始分支向上端分支過渡階段，說明當圓柱振動從非鎖定區進入鎖定區時，存在兩個相近頻率。當Ur=5時，圓柱振動由初始分支跳躍到上端分支，升力系數與阻力系數以及橫向運動幅值均有著較大的增加，橫向位移與升力系數處于同相位。當Ur=7時，圓柱振動從上端分支跳躍至下端分支了，由圖12(d)可知，進入下端分之后，升力系數與阻力系數以及位移均大幅度下降，升力系數與橫向振幅曲線由同相位變為反相位，出現“相位切換”現象。當Ur=9時，升力系數山腰處出現“小尖峰”現象，并且升力峰值左邊的小尖峰要高于右側的小尖峰，這是由于鎖定區存在三倍頻率分量導致的。當Ur=13時，圓柱脫離鎖定區，升力系數與阻力系數以及橫向振幅均急劇減小，阻力系數幾乎減小為0，升力與振動處于反相位角的情形。

(a)Ur=3 (b)Ur=4 (c)Ur=5

(d)Ur=7 (e)Ur=9 (f)Ur=13圖12 典型約化速度下升力與阻力隨時間變化曲線Fig.12 The lift and drag coefficients versus time in different Ur

圖13給出了采用勻減速初始條件時無量綱位移y/D升力系數Cl以及阻力系數Cd隨時間變化曲線，當Ur=13時，圓柱在鎖定區外，升力系數較小，阻力系數幾乎減小為0，并且升力與振動處于反相位角。當Ur=8時，圓柱下端分支中，升力系數依舊在山腰處出現“小尖峰”現象，升力與振動處于反相位角。當Ur=6時，圓柱由下端分支跳躍至上端分支，升力驟然增大同時阻力小幅度增大，升力與振幅由反向變為同相，出現“相位切換”現象。當Ur=5時，圓柱處于上端分支，升力系數與阻力系數增大，升力與位移表現為同相。Ur=4時，處于“初始分支”向“上端分支”過渡區域內，升力以及阻力系數出現了“拍”現象，當Ur=3時，升力系數與阻力系數回歸簡諧形式，升力與位移表現為同相。

(a)Ur=13 (b)Ur=8 (c)Ur=6

(d)Ur=5 (e)Ur=4 (f)Ur=3圖13 典型約化速度下升力與阻力以及橫向位移隨時間Fig.13 The lift and drag coefficients versus time in different Ur

2.4 從運動軌跡分析渦激振動

圖14給出采用勻加速方式時圓柱中心運動軌跡，圖中橫坐標為流向約化位移，縱坐標為橫向約化位移。當Ur=2時，主要發生流向振動，橫向振動幅值很小。當Ur=3時，圓柱橫向運動幅值增大，流向振動頻率變為橫向頻率兩倍，運動軌跡表現為扁平的“8”字型。當Ur=5時，圓柱進入上端分支，此時橫向與流向的運動頻率較為單一，圓柱表現為瘦長的8字型。當Ur=6.8時，圓柱振動軌跡表現出了超上端分支的特征。圓柱橫向振動大幅增大，8字型運動軌跡被拉扯為月牙形。當Ur=8時，橫向振動幅值急劇減小至0.7D，圓柱軌跡變為瘦長的8字型。當約化速度達到13.6時，此時圓柱振動已經脫離鎖定區，圓柱橫向振幅僅剩0.1D左右。

圖15給出了三種速度方式下各約化速度時的運動軌跡，通過觀察各約化速度下的運動軌跡可以清晰地認識到低質量比雙自由度圓柱渦激振動的振動形式衍化過程。對比三種方式可知，采用勻加速的數值模擬方式能夠很好的模擬出初始分支，上端分支，超上端分支以及下端分支的運動軌跡現象，其橫向振幅呈現遞增趨勢直至Ur=6.8，當Ur>6.8時，其軌跡突變為瘦長8字型。采用勻減速與勻速軌跡差異主要表現在5≤Ur≤6.8之間，勻減速軌跡在Ur>6時便突變為瘦長8字型。采用勻速方式時，在Ur>5時便突變為瘦長8字型。

(a)Ur=2 (b)Ur=3 (d)Ur=5

(f)Ur=6.8 (g)Ur=8 (h)Ur=14圖14 勻加速各約化速度下的軌跡圖Fig.14 The VIV trajectory versus time in different Ur

圖15 不同初始條件下圓柱渦激振動軌跡圖Fig.15 The VIV trajectory versus time in different initial conditions

2.5 從渦脫形式分析遲滯現象

圖16給出了勻加速初始條件下圓柱泄渦等值云圖(左為Jauvtis等試驗DPIV結果，右為CFD結果)。Ur=2時，處于初始分支中，每半個周期便會在圓柱一邊卸載一個漩渦，該泄渦模式為“2S”模式。Ur=5，處于上端分支中，每半個周期便會在圓柱一邊卸載一對漩渦，同時一個漩渦的渦量強度明顯大于另一個漩渦，該泄渦模式為“2P”模式。Ur=6.8，處于超上端分支中，每半個周期便會在圓柱一邊卸載三個漩渦，該泄渦模式為“2T”模式，當圓柱橫向得到超大振幅時，便會體現出該種泄渦模式。Ur=8時，每半個周期便會在圓柱一邊卸載一對漩渦，這兩個漩渦強度相當，該泄渦模式為“2P”模式。采用勻加速初始條件成功模擬出“2T”模式，這得益于考慮了渦激振動“遲滯效應”。

圖17給出了勻減速初始條件下圓柱泄渦等值云圖，Ur=6.8時，泄渦模式表現為“2P”模式，對比圖12(c)可知，當Ur=6.8時，采用勻加速與勻減速兩種初始條件下，圓柱尾渦模式不同，具體為：采用勻加速時，其尾渦為“2T”模式，與其較小Ur下的模式相同，而采用勻減速時，其尾渦為“2P”模式，與其較大Ur下的模式相同。勻減速Ur=6時，此時流體力超過尾渦維持“2P”模式的最大承受能力，其泄渦模式變為“2T”模式，該泄渦模式伴隨著較大的升力，從而導致振幅的突然增大。不同的尾渦模式下升力大小不同，從而導致橫向振幅不同以至于產生了“遲滯現象”。圖18給出勻速初始條件下圓柱泄渦等值云圖，Ur=5時，泄渦模式表現為“2P”模式，Ur=6.8時，泄渦模式依舊為“2P”模式。采用勻速初始條件時，圓柱泄渦一直表現為“2P”模式，該模式難以提供較大振幅，因此勻速初始條件未能捕獲上端分支。對比三種初始條件下的尾渦模式可知，圓柱的泄渦模式體現出“慣性”性質，尾渦的傾泄模式總有著維持原傾泄模式的趨勢，當約化速度提供的作用力大于圓柱維持原泄渦模式的最大承受能力后，圓柱泄渦模式將出現跳躍，不同初始條件對尾渦的影響進一步體現在振幅的差異上，同Ur下的不同泄渦模式導致產生“遲滯現象”。

(i)DPIV結果 (ii)數值模擬結果 (i)DPIV結果 (ii)數值模擬結果(a)Ur=3渦量等值云圖 (b)Ur=5渦量等值云圖

(i)DPIV結果 (ii)數值模擬結果 (i)DPIV結果 (ii)數值模擬結果(c)Ur=6.8渦量等值云圖 (d)Ur=8渦量等值云圖圖16 勻加速圓柱泄渦等值云圖對比圖Fig.16 The vorticity magnitude contours versus Ur in increasing condition

(a)Ur=6.8渦量等值云圖(b)Ur=6渦量等值云圖(a)Ur=5渦量等值云圖(b)Ur=6.8渦量等值云圖圖17 勻減速數值模擬圓柱泄渦等值云圖 圖18 勻速數值模擬圓柱泄渦等值云圖Fig.17 The vorticity magnitude contours versus Ur in Fig.18 The vorticity magnitude contours versus Ur in decreasing condition using CFD constant condition using CFD

2.6 加速度a對數值結果影響

由上節可知，不同初始條件下的渦激振動體現出很大的差異性，初始條件對圓柱泄渦模式有很大影響，當約化速度提供的作用力大于圓柱維持原泄渦模式的最大承受能力后，圓柱泄渦模式將出現跳躍，同時圓柱振動振幅將出現跳躍，以至于產生“遲滯現象”。增大速度時，圓柱泄渦將傾向于速度較小的泄渦形式。減小速度時，圓柱泄渦將傾向于速度較大的泄渦形式。由于流體具有慣性效應，因此采用勻加速和勻減速進行數值模擬研究是十分有必要的，本節將探討采用勻加速初始條件下，加速度對結果的影響。分別采用0.012 5，0.025，0.05以及0.1的約化加速度進行數值模擬，約化速度范圍為3～10，約化速度間隔為0.5，同時Ur=6.8為臨界點，也加以研究。

不同加速度下圓柱橫向振幅變化規律如圖19所示。采用四種加速度下，均捕獲到初始分支上端分支與下端分支。采用約化加速度為0.012 5，0.025的方式捕獲到了超上端分支。在3≤Ur≤5.5時，四種加速度方式得到的振幅基本一致，在該分支中，加速度對振動形態影響不大。在5.5

圖19 不同加速度下圓柱渦激橫向振幅Fig.19 Transverse max amplitude with different acceleration

圖20給出了不同加速度下升力均方根值與阻力均值變化曲線。在3≤Ur≤5.5時，四種加速度得到的升力基本一致。在5.5

(a)

(b)圖20 四種加速度下升力均方根與阻力均值隨約化速度關系Fig.20 The RMS lift coefficient and mean drag coefficient with different accelerations

圖21給出了不同加速度下遲滯區間變化曲線。采用約化加速度為0.012 5，0.025的方式捕獲到了遲滯區間，其范圍為6≤Ur≤6.8。采用約化加速度為0.05，0.1的方式沒有捕獲到超上端分支，其遲滯區間為5.5≤Ur≤6。由此可見，加速度大小對遲滯區間有較大影響，約化加速度在0.025～0.05存在一個臨界值，小于臨界值與大于臨界值的渦激振動遲滯區域不同。但同在大于臨界值或同在小于臨界值時，渦激振動得到遲滯區域相同。

圖21 不同加速度下渦激振動遲滯區域Fig.21 Hysteresis region of VIV under different acceleration

圖22給出Ur從6.5加速到6.8時升力阻力以及位移變化曲線，其采用約化加速度分別為0.025和0.05。可以看到，約化加速度為0.025時，升力系數與阻力系數隨著時間逐漸增加，而采用約化加速度為0.05時，升力系數與阻力系數隨著時間增加而陡然下降，同時對比橫向位移與升力系數可知，此時發生了相位切換。這說明采用較大加速度將會提前導致“相位切換”，從而使得振幅減小。

(a)a*=0.025

(b)a*=0.05圖22 Ur=6.8時下升力與阻力隨時間變化曲線Fig.22 The lift coefficient and drag coefficient versus time

3 結 論

本文基于PimpleDYMFoam求解器結合SSTk-ω湍流模型，進行了雙自由度低質量數值模擬研究，模擬采用了三種初始條件：勻加速，勻減速以及勻速條件。數值模擬捕獲到遲滯現象并且三種條件下圓柱振動響應有顯著區別，數值模擬對比得出結果如下：

(1)在低質量比圓柱渦激振動試驗中，采用加速與減速兩種試驗條件時，上端分支與下端分支存在遲滯。在“數值水池”中采用勻加速與勻減速方式也可捕獲遲滯現象。同時發現，采用勻加速與勻減速條件能捕獲到超上端分支，而采用勻速條件則缺失上端分支。在Ur=6.8時，勻加速方式得到最大振幅1.4D，而采用不考慮遲滯效應的勻速條件時，圓柱最大振幅僅為0.85D。由此可知，遲滯效應的存在對振幅的大小以及突變具有顯著影響。

(2)遲滯效應的機理可以通過泄渦模式來解釋，圓柱泄渦模式體現出“慣性”性質，尾渦的傾泄模式總有著維持原傾泄模型的趨勢，即增大速度時，圓柱泄渦將傾向于速度較小的泄渦形式。減小速度時，圓柱泄渦將傾向于速度較大的泄渦形式。當約化速度提供的作用力大于圓柱維持原泄渦模式的最大承受能力后，圓柱泄渦模式將出現跳躍。在遲滯區間內，同Ur下采用不同初始條件時的泄渦模式是不同的，同Ur下不同的泄渦模式導致了“遲滯現象”。

(3)采用勻加速勻減速以及勻速條件均捕獲到“鎖定”現象，但是鎖定區間不同。上端分支跳躍至下端分支的約化速度大小與初始條件有關。同時發現，當Ur≤4.2時，流向振動有兩個主要頻率，分別為單倍與雙倍橫向頻率。在鎖定區域內，橫向振動除主頻外，還存在一個3倍的低頻分量。

(4)作用在圓柱體上的升力與阻力也出現了遲滯現象，其遲滯區域為6≤Ur≤6.8，并在約化速度為6和6.8時，通過升力與位移關系捕獲了相位切換現象。升力與橫向位移剛開始為同向，隨著流速增加，泄渦模式發生突變導致圓柱受到的升力發生突變，從而導致升力與橫向位移變為反向，認為是泄渦模式的突變導致了相位切換。

(5)勻加速條件出現了“月牙形”運動軌跡，而勻減速與勻速只捕獲了經典“8”型運動。同時發現，在遲滯區間內，相同約化速度下的運動軌跡形式是不同的，圓柱軌跡也與初始條件有一定關系。

(6)在遲滯區域內，在約化加速度0.025與0.05間存在臨界值，大于該臨界值，升力與位移會提前發生相位切換，小于該臨界值，相位切換將會延后。數值模擬中，控制約化加速度小于等于0.025是其捕獲超上端分支的一個必要條件。

[ 1 ] 白治寧, 肖龍飛, 程正順,等. 深吃水半潛式平臺渦激運動響應模型實驗研究[J]. 船舶力學, 2014(4):377-384.

BAI Zhining, XIAO Longfei, CHENG Zhengshun, et al. Experimental study on vortex induced motion response of a deep draft semi-submersible platform[J]. Journal of Ship Mechanics， 2014(4): 377-384.

[ 2 ] 曹淑剛, 黃維平, 顧恩凱. 考慮流固耦合的彈性圓柱體渦激振動研究[J]. 振動與沖擊, 2015, 34(1): 58-62.

CAO Shugang, HUANG Weiping, GU Enkai. Vortex-induced vibration of an elastic cylinder considering fluid-structure interaction[J]. Journal of Vibration & Shock, 2015, 34(1): 58-62.

[ 3 ] 黃維平, 劉娟, 唐世振. 考慮流固耦合的大柔性圓柱體渦激振動非線性時域模型[J]. 振動與沖擊, 2012, 31(9): 140-143.

HUANG Weiping, LIU Juan, TANG Shizhen. Nonlinear model of vortex induced vibration of flexible cylinder in consideration of fluid-structure interaction[J]. Journal of Vibration & Shock, 2012, 31(9): 140-143.

[ 4 ] 范杰利, 黃維平. 細長立管兩向自由度渦激振動數值研究[J]. 振動與沖擊, 2012, 31(24): 65-68.

FAN Jieli, HUANG Weiping. Numerical simulation of 2-DOF vortex-induced vibration of a long riser[J]. Journal of Vibration & Shock, 2012, 31(24): 65-68.

[ 5 ] JAUVTIS N，WILLIAMSON C H K. The effect of two degrees of freedom on vortex-induced vibration at low mass and damping[J]. Journal of Fluid Mechanics, 2004, 509(509): 23-62.

[ 6 ] 谷家揚, 楊建民, 肖龍飛. 兩種典型立柱截面渦激運動的分析研究[J]. 船舶力學, 2014, 18(10): 1184-1194.

GU Jiayang, YANG Jianmin, XIAO Longfei. Study on vortex induced motion of two typical different cross-section columns[J]. Journal of Ship Mechanics, 2014, 18(10): 1184-1194.

[ 7 ] GUILMINEAU E, QUEUTEY P. Numerical simulation of vortex-induced vibration of a circular cylinder with low mass-damping in a turbulent flow[J]. Journal of Fluids and Structures, 2004, 19(4): 449-466.

[ 8 ] 陳威霖, 及春寧, 徐萬海. 并列雙圓柱流致振動的不對稱振動和對稱性遲滯研究[J]. 力學學報, 2015, 47(5): 731-739.

CHEN Weilin, JI Chunning, XU Wanghai. Numerical investigation on the asymmetric vibration and symmetry hysteresis of flow-induced vibration of two side-by-side cylinders[J]. Chinese Journal of Theoretical & Applied Mechanics, 2015, 47(5): 731-739.

[ 9 ] KIM S, WILSON P A, CHEN Z M. Numerical simulation of force and wake mode of an oscillating cylinder[J]. Journal of Fluids & Structures, 2014, 44(7): 216-225.

[10] KHALAK A, WILLIAMSON C H K. Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping[J]. Journal of Fluids & Structures, 1999, 13(7/8): 813-851.

[11] MINGUEZ M，LUPPI A，BERGER A. Slender buoy FSHR vortex induced rotations[C]// Proceedings of the ASME 31th International Conference on Ocean, Offshore and Arctic Engineering. Rio de Janeiro: OMAE, 2012.

[12] CHEN W, JI C, XU W, et al. Response and wake patterns of two side-by-side elastically supported circular cylinders in uniform laminar cross-flow[J]. Journal of Fluids & Structures, 2015, 55: 218-236.