例談小學數學學科內課程整合的實施策略

姚榮金

【摘 要】小學數學學科內課程整合實施是指小學數學課程內的教學目標、教學內容、教學方法的整合，也即指課程實施過程中內容與資源的整合。具體而言，小學數學學科內整合可以劃分為以下幾類：1.重組式課程整合，主要應用于教學內容的整合；2. 相關式課程整合，主要是對運用相同數學思想方法、前后相關聯的課時進行整合；3. 根源式課程整合，主要是根據學生學習基礎，以及知識間的聯系對復習課進行相關整合。課程整合其實是一個梳理的過程，在具體實施過程中，教師可以采取對應策略有效展開，讓學生聯系著學知識，自主建構個體獨特的知識網絡。

【關鍵詞】小學數學；課程整合；實施策略

整合就是通過協調、融合，將零散的要素組合在一起。《浙江省教育廳辦公室關于促進義務教育課程整合的指導意見》（浙教辦基〔2015〕79號 ）文件指出：課程整合實施是指課程內和課程間的教學目標、教學內容、教學方法的整合，也指課程實施過程中課內外的整合……學校應根據教學實際，從學科內的局部整合到學科間的主題整合，再到“全課程”的統整，逐步推進。由此可見，小學數學學科內課程整合實施是指小學數學課程內的教學目標、教學內容、教學方法的整合，也即指課程實施過程中內容與資源的整合。在深化課改的進程中筆者發現課程整合實施是當前學校深化課程改革的主要途徑之一，學科內課程整合實施是學科教師努力實踐的基礎。圍繞立德樹人目標，針對學生身心發展特點，依據國家課程標準與學生核心素養要求，筆者對小學數學相關課程內容進行整合實施，以期增強課程實施的綜合性和實效性。

一、重組式課程整合實施策略

重組式課程整合主要應用于教學內容的整合。舉個例子，六年級是小學學習階段的最后一年，學生所學的數學知識比以往更綜合、更復雜、知識間聯系更密切。根據學生已有認知基礎和數學知識間的聯系，筆者對六年級數學教材進行梳理，科學、合理地調整課時內容，進行重組式課程整合實施。以六上第一單元“圓”為例，通過對知識點的整理我們把這一單元中的內容作了4個調整，具體如下。

第一個調整：“圓的認識（一）”第一課時的目標是在畫圓的過程中，理解同圓中半徑、直徑以及直徑和半徑之間的關系，體會圓心和半徑之間的關系；“圓的認識（二）”的目標是探索并發現圓是軸對稱圖形、有無數條對稱軸，體會圓的對稱性。兩課時都是在學習圓的特征，而且圓的對稱軸剛好和直徑有必然的聯系，這兩課時整合成了一課時，學生學習更有效。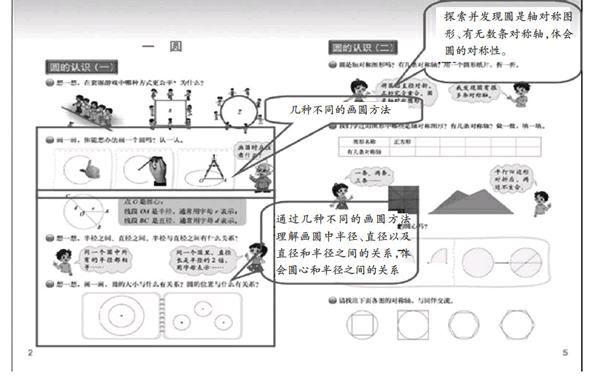

第二個調整：“圓的認識（一）”第二課時和欣賞與設計整合成一課時。有利于學生理解圓的特征與生活的聯系，提高學生根據圓的性質進行問題解決的能力。

第三個調整：圓周率的數學文化知識與圓的周長學習整合為一課時。當討論圓的周長和直徑間有什么關系的時候，可以出示圓周率歷史中的三種方法，以閱讀的形式讓學生了解有哪些方法可以知道周長和直徑間的關系，然后由學生選擇一種好操作的方法進行驗證，最后出示圓周率的歷史這一課中有關的一些數據。數學文化與知識有機整合才具有生命活力，才是學生進一步學習數學的原動力。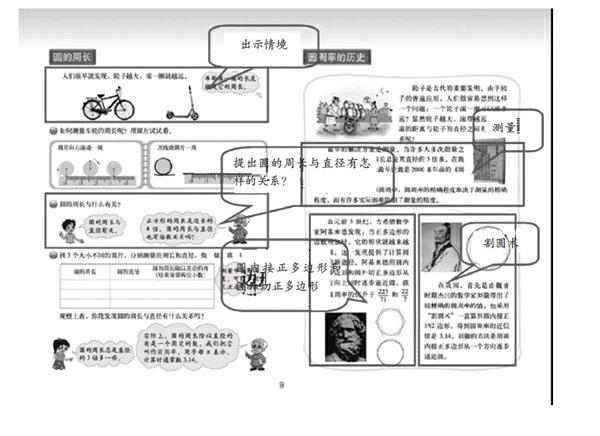

第四個調整：“圓的面積（一）”第一課時主要是結合實例認識圓的面積，并經歷圓面積計算公式的推導過程。除了把圓轉化成平行四邊形外還有很多其他的方法，可以把“圓的面積（二）”中的例三將圓形的墊片剪開恰好是一個底為圓的周長、高為圓的半徑的三角形以及練一練第三題將圓形的墊片剪開得到兩個近似的三角形，再拼成一個底為圓的周長的一半、高為圓的半徑的平行四邊形整合在一起，有利于學生體會通過轉化成不同的圖形都可以推導出圓的面積等于πr2。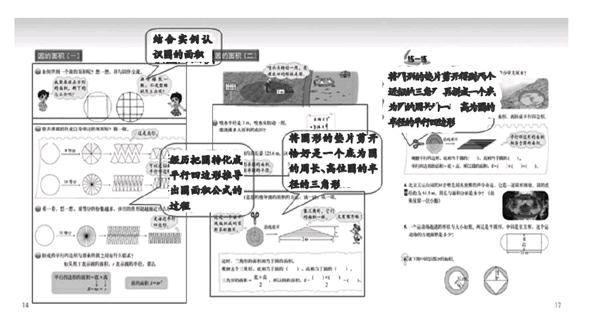

二、相關式課程整合實施策略

對運用相同數學思想方法、前后相關聯的課時進行相關式課程整合實施，有利于學生綜合有效地掌握知識，更能觸類旁通，舉一反三。

例如，五年級上冊第三單元的“找因數”和第三單元的“找質數”可以整合為一節40分鐘的課。“找因數”這節課，學生要學會在1～100的自然數中，找到某個自然數的所有因數，“找質數”正是根據因數的個數把自然數（0除外），分成質數、合數和1，因而這兩節課可以整合成一節課。在教學時，當學生掌握找一個數的所有因數方法后，出示15、21、3、4、5、7、9、45、1這樣一組數，讓學生根據因數的個數，把這些數分成兩類，并追問：你們是怎么分類的？引出“質數”和“合數”的概念，并提出1既不是質數也不是合數。

例如，在上完第四單元的“平行四邊形的面積”和“三角形的面積”這兩節課的第一課時后，這兩節課的“試一試”可以整合成一節40分鐘的課。兩節課的“試一試”運用的數學思想方法是一樣的，第1題都是用公式的逆運用和列方程這兩種方法解決問題的，第2題讓學生通過計算明白“同底等高的平行四邊形、三角形的面積是相等的”。而且學生在學習完平行四邊形后，根據知識的遷移，能更好、更快地掌握三角形的知識。

例如，六上第二單元的“分數的混合運算（二）”的主要目標是結合具體情境，會畫圖表示“增加幾分之幾”或“減少幾分之幾”的意義及計算，而“百分數的應用（二）”的目標也是會畫圖表示“增加百分之幾”或“減少百分之幾”的意義及計算，在解決問題的策略上是一樣的，正因為在分數中已經具體學習了用這樣的策略解決這類題，那在百分數計算中就可以縮短時間，因此，筆者認為可以把“百分數的應用（二）”的2課時縮短為1課時。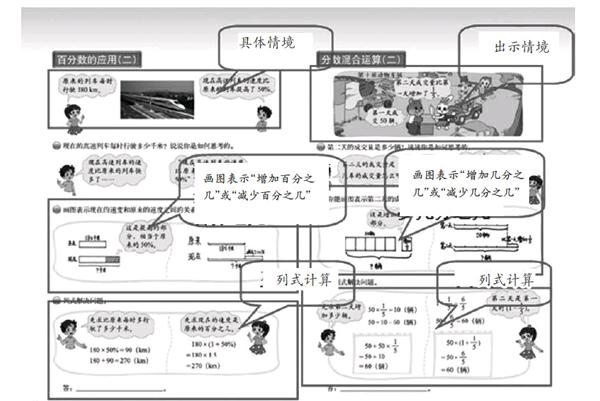

又如，“分數混合運算（三）”和“百分數的應用（三）”也是這樣，我們可以具體來看一看。都是通過畫圖、找等量關系、列方程解決此類問題，因此我們覺得同樣可以把“百分數的應用（三）”的2課時整合成1課時。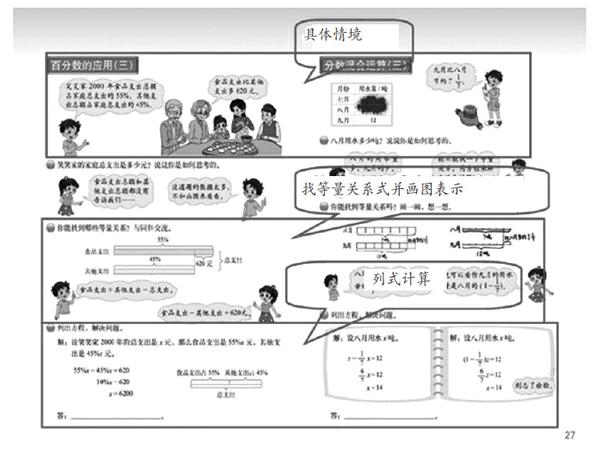

在實踐中，這樣的教學既節省了時間，又有利于學生理解、掌握知識，學生學得有效、輕松，教師教得順手、舒心。

三、根源式課程整合實施策略

關于復習課，筆者是根據學生學習基礎，以及知識間的聯系，進行根源式的整合實施的。例如，總復習，教材中是把復習整數和復習小數、分數、百分數分開來的。事實上，可以把這兩部分整合在一起復習，因為不管整數、小數、分數還是百分數，其實這些數都具有同根源的共通點，教師可以從數的意義、組成、計數單位等方面復習，比如整數部分的個位上的數表示幾個一，十位上的數表示幾個十，百位上的數表示幾個百，小數部分的十分位表示幾個0.1，百分位表示幾個0.01，而分數同樣有自己的分數單位，理解了數的意義就可以比較數的大小，進一步梳理整數、小數的數位順序表及相關知識，接著可以復習數的屬性等，比如奇數、偶數、質數、合數、公因數、公倍數等。等梳理完這些知識點后，讓孩子靜下心來安安靜靜地完成后面相對應的作業，對于基礎好的同學可以另外增加一些挑戰題，最后針對錯誤率高的題目進行分析總結。

例如，圖形與幾何領域的復習，可以引導學生感悟“點、線、面、體”之間的關系。以點可以做端點，引出線段、射線；點可以做頂點，引出角；點還可以做起點；等等。讓學生體會點運動成線、線運動成面、面運動成體，溝通各種圖形之間的聯系，最后建構“圖形與幾何”的知識網絡。

小學數學課程整合其實是一個梳理的過程，把所有相關聯的知識連成線，形成知識脈絡，通過多階、多維地梳理，讓學生聯系著學知識，自主建構個體獨特的知識網絡。

（浙江省浦江縣教育研究與教師培訓中心

322200）endprint