培養小學一年級學生數感的探索與反思

徐丹

【摘要】良好的數感有助于學生理解現實生活中數的意義，理解或表述具體情境中的數量關系。本文介紹培養小學生數感的三種做法：在具體數學情境的數數中建立數感、在不斷聯系的運算中發展數感、在解決實際問題中增強數感。

【關鍵詞】數感 實踐 思考 數量關系

【中圖分類號】G 【文獻標識碼】A

【文章編號】0450-9889（2017）09A-0075-03

數感主要是指關于數量、數量關系，運算結果估計等方面的感悟。建立數感有助于學生理解現實生活中數的意義，理解或表述具體情境中的數量關系。數感好的學生，主要表現為在運算中不拘泥于運用計算法則或公式進行計算，而是能夠根據數的特征，靈活地選取計算策略。

教師對數感一詞并不陌生，但對數感的培養卻存在認識上的缺失：其一，認為數感培養是某些課的教學目標；其二，重知識技能落實輕數學素養的發展。

實際上，培養學生數感是一個長期積累的過程，學生的數感在入學前已經萌芽，需要教師充分挖掘教學資源，對教材資源進行重組與拓展，精心設計教學環節引導學生的思維，在日常教學中幫助學生建立數感、發展數感、增強數感。

一、在具體數學情境的數數中建立數感

數是抽象的數學符號，一年級的學生對數的認識依托于具體的情境。比如說數字“2”，學生頭腦中可能會出現2顆糖果，2枝鉛筆，也可能是3個小朋友走掉了1個還剩2個等具體情境。一年級學生的思維方式以具體直觀的形象思維為主，他們在具體的生活情境中比較容易理解數的含義以及數與數之間的關系。學生認識數的過程離不開數數。數數是一項內涵豐富的數學活動，它可以體現學生對數的順序、數與數之間關系的理解。數學教學可以在學生原有生活經驗的基礎上，選擇特定的數學情境，讓學生在有趣的數數活動中建立數感。

（一）實物情境圖

數學源于生活，生活中的很多情境都值得用數學的眼光進行觀察和分析。在數數活動中，選取恰當的生活情境，有助于學生體會到數數方法的多樣性，以及選擇合適的數數方法的必要性和簡便性。要讓學生看到一幅圖就能立刻對數數策略做出恰當的選擇，依靠的是對數的直覺反應，即學生的大腦已經能夠做出無意識的反應。

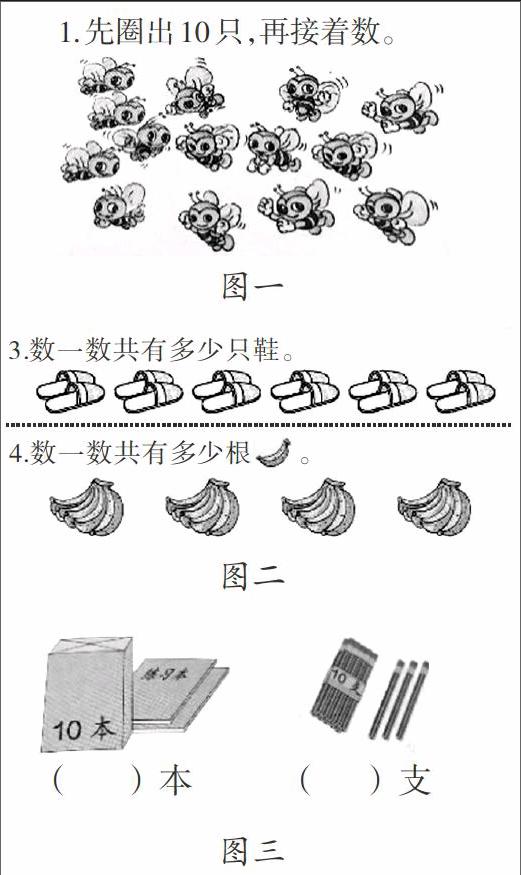
1.先圈出10只，再接著數。

上述三幅圖都出現在人教版一年級上冊《11～20各數的認識》課后練習十七，要求學生數出圖中物品的數量。圖中物品的呈現方式是不一樣的，所需要的數數策略也有所不同。學生對數的認識從一位數擴展到了兩位數，數變大了，同時還產生了位值的概念。這是讓學生初步感受數數策略，建立直覺性數感的好時機。筆者在教學過程中設計了如下環節：

師：老師這里有三幅圖，比一比，誰能又快又準確地數出圖中物品的數量。

（學生獨立數數，老師巡視）

師：說一說每一幅圖你是怎么數的。

生1：第一幅圖的蜜蜂有點亂，我是1只1只邊做記號邊數的，一共是14只。

生2：第二幅圖拖鞋一雙一雙地擺，我是2，4，6……這樣2個2個數的，一共是12只。香蕉是5根一柄，我是5、10、15、20這樣5個5個數的，一共20根。

生3：第三幅圖我是看一包書上面寫著10本，旁邊還有2本，一個“十”和2個“一”合起來就是12本，數筆的方法也一樣。

師：小朋友們真會觀察，數數的方法有很多，可以1個1個數，2個2個數，5個5個數……也可以分別數出幾個“十”和幾個“一”再合起來。根據不同的圖選擇合適的數數方法，就能數得又快又準確。

同樣是數數，不同的情境圖可以選擇不同的數數方法，教學中教師巧妙地將練習中的幾道題進行整合，讓學生在對比中做出合理的選擇，學會舉一反三。通過長期的積累，學生頭腦中建立了很多數數方法的模型，一旦遇到類似情況就能做出直覺反應。這是學生數感建立的重要標志。

（二）變化幾何圖

數與形是數學中兩個最基本的研究對象，數可以使形的表達更精確，形可以使數量關系的表達更清晰。在一年級的數學教學中，將抽象的數與幾何圖形的拼組相結合，學生的數數伴隨著空間想象，每個孩子的觀察角度有所不同，數數方法也不一樣。學生的數數方法都有明顯的個體性特征。

如圖四，數圖中灰色的三角形數量，有的學生是一行一行地往下數，每一行都是前一行的基礎上加1個，第四個圖形就是“1+2+3+4”個；有的學生斜著觀察，第四個圖形就是“4+3+2+1”個。如圖五，有的學生是從每行和每列的數量變化進行觀察的，接下去應該是五行五列，可以5個5個快速數出是25；有的學生是對前后兩個圖進行重疊式的對比，發現每次都多了一行和一列（行與列有一個重疊），接下去就是“16+9=25”個。

讓變化的幾何圖作為數學情境，能夠促使學生通過觀察和對比形的變化來感知數量的變化，認識到數數不一定是幾個幾個數，也可以遵循一定規律變化著數，數數的方法更多樣了。在數數中，學生學會了觀察，逐漸建立直覺的、個體性的數感。

二、在不斷聯系的運算中發展數感

一年級數學教材遵循從小到大、由易到難的教學原則，以10、20、100作為分界點，讓學生循序漸進地認識數，以及學習加減法運算。教材按照運算的復雜程度，每次都是先學不進位加法和不退位減法，再學進位加法和退位減法；不論數有多大，加減法運算遵循的都是位值和十進制等數學法則。教材這樣安排遵循學生身心發展規律，便于學生循序漸進地掌握運算法則，但是也容易使學生在頭腦中將加減法運算割裂成一個個獨立的部分，從而導致在計算過程中只會依賴運算法則進行機械的運算，而不能根據數字的特征尋求簡便的運算方法，不利于學生發展數感。因此，教師在教學中要整體把握運算教學的目標，借助體現數量關系的圖溝通不同運算之間的關聯，通過設計開放性的計算練習建立關聯數字組，通過開展發散性的轉換訓練實現式與式的關聯，從而發展學生的數感。endprint

（一）借助直觀圖建立關系模型

每一種運算都不是孤立存在的，彼此之間存在內在邏輯聯系。一年級數學涉及的加法和減法之間是互逆關系。在計算20以內退位減法時用想加做減法可以快速地計算出得數，如計算12-9=（ ），只要想9+（ ）=12就能算出結果。一年級學生剛剛學習加法和減法，有必要在教學中及時溝通加法和減法之間的關系。抽象的內在聯系可以借助體現數量關系的直觀圖來溝通，在學生頭腦中建立加減法關系的模型，發展學生的數感。

在教學“6、7的加減法”時，學生學習了“一圖四式”（人教版一年級上冊P42，根據一幅圖寫出兩道加法算式和兩道減法算式），這時再引入表示數量關系的圖，就能使學生在腦海中建立加減法關系的圖像模型，為運用加減法之間的關系進行運算奠定基礎。

師（出示6個正方形）：涂一涂，將6個正方形分成2個部分，你打算涂幾個（見圖六）？

生1：涂4個。

師：（根據學生的回答出示圖七），揭示“6”可以分成“4”和“2”，看圖你能寫出哪些算式？

生：4+2=6，2+4=6，6-2=4，6-4=2。

師：圖中老師能找到算式中的“4”和“2”，“6”表示什么意思呢？

生：“6”是總共有6個正方形。

師：（出示圖八）這樣可以更清楚地看出6、4、2這三個數之間的關系。

師：（出示圖九）現在你還能看出這三個數之間的關系嗎？

生：能。

師：（出示圖十）你能根據這幅圖來寫一寫算式嗎？

生：△+☆=10，☆+△=10，10-△=☆，10-☆=△。

學生頭腦中有了圖十這樣直觀的圖像模型，數與數之間的關系一目了然，而數與數之間關系的不同表達式就是加法與減法之間數量關系的轉換。學生根本不需要去記“加數=和-加數”“減數=被減數-差”等這些枯燥的表達式就能運用自如，數感在這樣的聯系中得到發展。

（二）借助開放性式題建立關聯數組

“20以內退位減法”在減法計算教學中占有舉足輕重的地位，20以內退位減法的熟練程度直接影響到今后多位數減法的計算正確率。很多教師認為，熟能生巧，因而試圖通過不斷的強化訓練來提高學生的計算正確率，但是實際上學生的數感并沒有在重復的機械訓練中獲得發展。在學習“20以內退位減法”時，教材介紹了三種計算方法，如“12-9”：個位上“2-9”不夠減，可以采用破十法，直接用“10-9=1”，再算“1+2=3”；也可以采用連減法“12-2-7=3”；還可以采用想加算減法，想“9+（3）=12”，那么“12-9=3”。學生能夠理解算理，也能夠運用這些算法進行計算，但是這幾種算法都需要幾個步驟，學生在口算時要想好幾個步驟，想達到一定的速度和正確率頗有難度。根據退位減法的算理，我們可以設計開放性式題，讓學生在填寫式題時鞏固算法，同時又能關注數字本身的特征，在頭腦中建立一些相關聯的數字組，在計算中加以運用，從而發展數感。

師：（出示式題□-7=□，見圖十一）給大家2分鐘時間，看誰填出的算式多。

師：同學們都能夠有順序地思考。觀察這些算式，你有什么發現？

生1：被減數一個一個地增加，差也一個一個地增加。

生2：有些是不退位減法，有些是退位減法。

生3：被減數的個位和差都相差3。

師：你知道為什么會相差3嗎？

生4：我想這是破十法中的3，比如11-7，先算10-7=3，再算3+1=4。

（其他學生按照這個思路去觀察，發現如果用破十法去計算，都會先算“10-7=3”）

片段四：

師：（出示式題二 □-□=7，見圖十二）給大家2分鐘時間，看誰寫的算式多。

師：同學們都能夠有順序地思考。觀察這些算式，你有什么發現？

生1：被減數一個一個地增加，減數也一個一個地增加。

生2：被減數的個位比減數小3。

師：你知道為什么會相差3嗎？

生3：比如11-4，我們用連減法，把4分成1和3，11-1=10，10-3=7。

（其他學生按照這樣的思路去觀察，發現減數都可以分成被減數的個位數字和3，這樣連減的第二步算的都是“10-3=7”）

上述兩個式題中的已知數都是“7”，不論“7”是差還是減數，學生發現計算中都會用到“10-7=3”或者“10-3=7”。在有關“7”的減法中，學生會習慣性地將“3”與之進行聯系，形成一種思維習慣，這便是一種數感。填數練習還可以進一步擴展，如□-□=6與□-6=□，學生會發現“6”與“4”的密切關系。這樣的填數練習，既是對20以內減法的鞏固，又能讓學生跳出算法本身的桎梏，關注到數字本身，在頭腦中建立一組組相關聯的數字，如“7”與“3”，“6”與“4”。在今后更復雜的運算中，學生如果將數字的這種關聯性進行運用，就會使得數感在運算中不斷發展。

（三）借助發散性的轉換建立式與式的關聯

運算教學螺旋上升，學生并不是不斷學習新的算法，而是不斷地將新的運算轉化成已經學過的運算。如一年級100以內進位加法可以轉化成20以內進位加法來計算，今后要學的多位數加法可以轉換成100以內加法進行計算等。轉換的方式具有多樣性，如在計算“24+9”就有多種轉換方法：方法一，先算“4+9=13”，再算“20+13=33”；方法二，先算“24+6=30”，再算“30+3=33”；方法三，先算“29+1=30”，再算“30+3=33”；方法四，“24+10=34，34-1=33”等。這些算法都將進位加法進行拆分和重組，都是建立在很多已知算式的基礎之上進行計算的。開展發散性的轉換訓練，讓學生將一個算式進行多角度的轉換，有助于學生建立算式之間的關聯，在復雜的計算中靈活選用算法，提高計算的速度和正確率，發展數感。

在不改變運算結果的前提下，學生根據數字之間的關系，不斷變換觀察角度，將比較復雜的計算轉換成簡單的心算（如圖十三、十四）。轉換訓練可以由學生獨立完成，訓練學生的思維廣度；也可以由一個學習小組成員共同完成，分享彼此的成果。在不斷求異的轉換中，學生對數與數之間的關系有了更敏銳的感覺，并把這種感覺應用于式的運算中，建立式與式的關聯。學生的數感在這種訓練中不斷發展。

三、在解決實際問題中增強數感

運算與解決問題緊密相連，因此我們要引導學生依托具體的情境來理解運算的含義，在解決問題的過程中掌握運算技能。學生解決一個問題需要經歷提取信息、選擇算法、得出結論這一基本過程。在這一過程中，理解數的含義，提取數量關系，得出結論需要學生綜合運用對數的認識、數的運算以及對數量關系的把握等知識。學生的數感在解決問題中得到體現并增強。

圖十五是人教版一年級下冊P80的一道題，一群小朋友圍在桌子旁邊分蛋糕，桌子上放著3盤蛋糕，每盤都是6個，一個小朋友說，分給17個小朋友，問：每個小朋友分一塊，夠嗎？圖中只出現了11個小朋友，而小朋友說要分給17個小朋友，學生首先需要對人數做出判斷。要知道每個小朋友分一塊夠不夠，可以將人數與蛋糕的數量進行比較，根據比較結果做出判斷。

學生能夠把握將人數和蛋糕數進行比較來做出判斷的基本思路，根據個人對題目中“3個6”“18”“17”這幾個數的特征的把握，綜合運用加法、減法以及比較數的大小等來表示自己的想法，并依據計算結果做出判斷。正確的計算是做出正確判斷的前提，但也可能計算正確，在判斷時沒有理清數量之間的關系而做出錯誤的判斷。數感在結論的判斷中得到增強。

數感的培養是一個長期積累的過程，需要教師在日常教學中深入研讀教材，挖掘教材資源，在課堂上進行不斷的滲透；需要教師整體把握教材的螺旋上升特征，在課堂教學教學中做好孕伏和聯系；需要教師重視解決問題策略的多樣性，鼓勵學生靈活和創造性地解決問題，讓學生在潛移默化中培養和發展數感，最終提升數學素養。

（責編 黎雪娟）endprint