讓創新意識在自由探索中生根發芽

【摘 要】培養學生的創新意識是教育教學的重要目標，因此，教師可以通過自由探索氛圍的營造，使學生想探索，培育創新意愿；保證充分自由探索的時間，靜待創新之花的盛開；提供指向本源的可選擇的自由探索材料，結出創新之果；形成氛圍、時間、空間的“創新場”，讓學生的創新意識生根發芽。

【關鍵詞】創新意識 自由探索 氛圍 時間 空間

數學學習中，“喚起學生的創新欲望，激發學生的創新思維，經歷創新性學習的過程”已成為當下數學教師的普遍共識。“營造獨立思考、自由探索的良好環境” 能有效培養學生的創新意識，這儼然成為一線教師的普遍教學意識。怎樣從操作層面使學生在課堂上自由探索，讓創新意識在學習中生根發芽，進而開花結果？筆者結合自己的教學實踐談些具體做法。

一、營“自由探索”氛圍，育創新之意

教師在數學教學時應創設一種能讓學生自由探索的教學氛圍，并適當鼓勵以激發學生創新的欲望與興趣。

首先，創設不唯師、不唯書的氛圍。創新的核心要素是質疑的品質與意識。在課堂學習過程中，當學生的認識與教師、教材答案產生沖突時，是全盤接受還是在挑戰權威中學習，這既關系到學生對知識的真理解，更關系到學生質疑品質的培養。

其次，鼓勵爭論自由。表現在數學課堂上的自由爭論，既可以和教師爭論，也可以和同伴爭論。通過爭論，形成共鳴，或相同，或相異，都已不是主要目的，爭論過程中學生養成自由探索意識，提升自由思維品質尤顯重要。

例如，五年級下冊的單式折線統計圖，我們改編材料（如圖1）。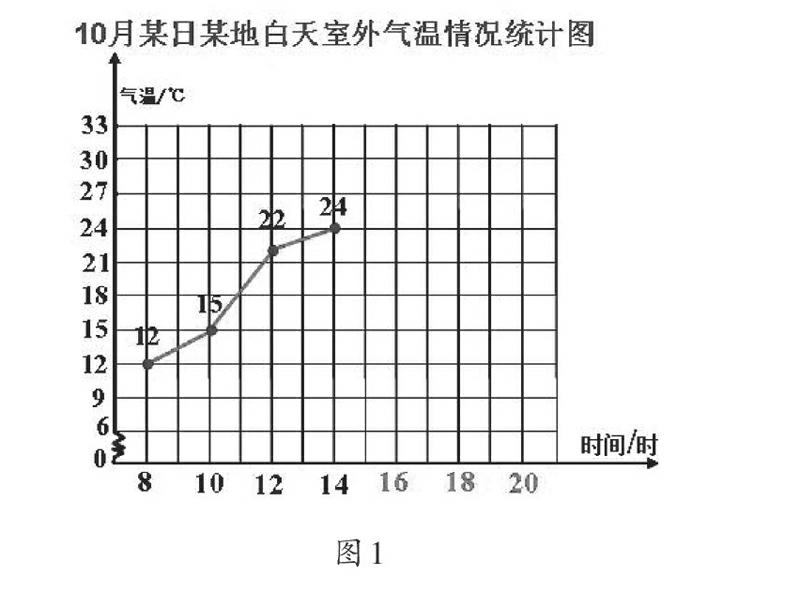

（1）引導學生觀察例題中的折線統計圖。

（2）根據觀察到的結果，估計16時、18時、20時的氣溫，并將統計圖補充完整。

（3）展示學生畫法，并開展自由爭論。

學生展示作品中的折線有繼續升高的變化情況，也有折線向下氣溫向下變化的。接著教師鼓勵學生自由爭論，通過爭論大家認識到，從發展趨勢上看氣溫不斷升高，但可能會受太陽光照等影響，氣溫在下午2時可能最高，其折線統計圖變化趨勢一般會逐漸下降；如果碰到極端天氣則可能在某一時間快速下降或上升。

最后，鼓勵自由質疑。小學生尤其是低年級的學生是很喜歡問為什么的，但在課堂上卻往往是有質疑問難時間，無質疑問難之人。學生不敢問、不想問、不會問的現象較為普遍。究其原因，與其有無自由質疑的機會與氛圍相關。

為培養學生自由質疑的習慣，教師一般從接手一個班級開始的第一個學期起專門在課堂上留下至少5分鐘時間進行質疑問難，告訴學生：現在是質疑時間，請大家對剛才老師或同學的觀點及學到的知識進行自由質疑。開始實施時一般提供方法供學生參考，如怎么提“為什么”。教師提出：你有提為什么的自由，你既可以針對自己不懂的內容，也可以針對其他同學可能會不懂的內容。接下來，我和學生共同商議，任何學生可以在任何時候、針對任何內容提出質疑。

這樣，學生知道質疑既是自己的一種權利，也是一種自由。而為質疑做準備，既需認真傾聽他人觀點，還需主動思維，尋求自己個性化的方法，從而達到逐步培養學生創新意識的目的。

二、留“自由探索”時間，開創新之花

一個人的創新能力并不是一朝一夕所能形成的，也不是某一節課所能培養的，這是一個長期的過程。但并不是說在課堂學習中對于創新能力的培養無所作為，我們要做的是在學生自由探索時留足時間，保護學生的求異思維，激發學生的創新欲望。這如同埋下創新的種子，讓它在合適的時間、合適的“溫度”下生根發芽。

（一）留足學生自由探索的時間

教師要舍得花時間去等待學生的“慢”探索。在學生探索的過程中一般不指導、不暗示，盡量讓學生自由探索。如碰到困難應由學生主動提出，教師給予鼓勵與少量點撥。

如在教學人教版一年級下冊第86頁數學游戲時（如圖2）。

課后，李同學對這道題興趣高漲，主動請筆者再出題考考他。筆者先出一個：第20幅圖是什么動作？他想了一會兒，回答與第二幅圖相同，又要筆者出更難的題目。再出了個61，他回到座位上，寫寫、畫畫，也正確地解決了問題。

筆者接著問他第88幅、第123幅、第800幅分別是什么動作。雖然他探索的時間都較長，但在耐心等待下，除第123幅圖的動作錯了，其他都對。

他是怎么探索的？首先在探索的過程中找到整十、整百時圖形的變化規律，再從最接近的整十、整百開始快速解決問題。如10、20、30分別與1、2、3的動作一樣，100、200、300也分別與1、2、3的動作相同。找到了1到9的動作變化規律，就找到了10到90及100到900的變化規律。

實際上他在頭腦里創造了一張“3的倍數”（雖然他并不知3的倍數）與余數模型圖，如同一張數的網格圖（如圖3，筆者依據該學生的描述所畫），再在頭腦里運用這個模型圖快速檢索得到答案。

如883，先從880開始確定與第一幅圖的動作一樣，則881、882幅圖分別對應的是第二、三兩幅圖，這樣依次重復下去。

筆者驚嘆他的創新性思維，也暗暗慶幸自己不暗示、不提示，讓他有充分的自由探索時間，才開出如此美麗的創新之花。

（二）留足學生自由展示的時間

展示學生的探索成果，有利于學生之間開展有針對性的自由爭論，從而激發學生的學習興趣，進而借鑒同伴間解決問題的創新性方法與過程，提高學習成效。

如教學人教版二年級上冊“乘法初步認識”時，課后練習有這樣一道題：endprint

“請任意寫一道乘法算式，并畫圖表示所寫乘法算式的意思。”在學生自由寫乘法算式、畫乘法意義后，筆者留足展示學生作品的時間，課上出現了許多精彩的想法。

生：我寫的乘法算式是“4×5=20”，我先一行畫了4個圓圈，畫了5行，表示5個4的和是20；也可以理解成一豎（列）有5個，有4豎（列），表示4個5的和是20。

生：我寫的乘法算式是“9×9=81”，我是結合買玩具來理解的，我買跳跳球，一個9元錢，我買了9個，要付的錢是9個9元。

生：我寫的乘法算式是“1×1=1”，我是用圓圈表示的，就在本子上畫出1個圓圈就行了，最簡單，表示1個1是1。

生：我是用叉叉表示的，一行先畫幾個叉叉，在中間用省略號表示，我就表示100個叉叉；再豎著也用省略號表示，表示100行，這個算式的意思是有100個100。也可以這樣想，這個叉表示一種外星文字，一行是100個，有100行，一共有100個100等于10000個外星文。所以算式是“100×100=10000”。

生：我這個最有趣了，我是在這個方框內用圓圈表示0×0=0，你看到了什么嗎？一個都沒有，就表示0個0。

生：我表示的算式是0×3=0，今天3個人想吃大餅，每人0個大餅，這3個人共吃了3個0，還是0個大餅。

生：我寫的算式是X×X=X，我的圖有無數種畫法，因為X可以代表3、代表0，也可以代表100，也就是不管代表什么數都可以的意思。所以我這個算式把你們剛才畫的圖與意思都包括在里面了。

……

因為留足了學生自由展示的時間，每個學生都有機會將自己個性化的想法展示出來。展示的過程既是建立乘法意義直觀模型的過程，也是展示自己獨特個性的過程。這樣的過程有利于激發學生的學習興趣，喚醒學生標新立異的創新性思維，這對培養學生的創新意識很有好處。

三、創“自由探索”空間，結創新之果

培養創新意識，除了有效的激勵措施，充分的探索時間，還需要創設“自由探索”的空間，讓學生能在富有彈性的自由探索的空間內產生個性化的解決方法，從而體會到創新之快樂。要做到這點，就要依賴教師所設計的開放性學習材料，主要有兩點。

（一）呈現選擇性探索材料，讓學生有自由選擇的機會

尊重學生的自由選擇權能激發學生的探索動力，進而促進學生去主動創新。而尊重學生的選擇權，首先教師必須要提供讓學生有選擇機會的開放性、富有彈性的學習材料，學生再結合自身的學習能力、知識基礎選擇適合自己探索的材料開展研究。

例如三角形內角和的教學，筆者是這樣進行的。

（1）師生交流學法。課始通過師生交流，了解到運用與新課相關的舊知識通過轉化的方法學習新知，是常用的學習方法。

（2）揭示學習內容“三角形的內角和”，并指出三角形內角和分別所在位置與意思。討論與本課新知有關的舊知識分別有哪些，共同推測可能有如下相關知識：用量角器量角、特殊角度數（平角180°，直角90°，周角360°）、長方形內角和90°×4=360°。

（3）呈現材料。

材料一：呈現銳角三角形、直角三角形、鈍角三角形等圖形各一個。

材料二：呈現銳角三角形、直角三角形、鈍角三角形紙片若干個。

（4）選擇材料和探索方法。

任選兩組材料中的一個或幾個三角形，再任選所運用的一種或兩種舊知識探索其內角和。

（5）學生自由探索（過程略）。

在上例中，學生探索的材料是自己選擇的，探索的方法也是自己選擇的，因為選擇，所以喜歡，因為喜歡才使學生的探索富有成效，有通過量內角和解決問題的，也有拼成長方形研究直角三角形內角和的，還有把三個內容拼成平角研究內角和的……每位學生都有了自己獨特的創造性的想法，課堂也結滿了創新之果。

（二）呈現本源性探索材料，讓學生有自由思維的空間

促進學生學習的材料主要有兩類。一是基于包含其前位知識的帶有暗示探索過程的學習材料，這種學習材料主要指向于學生新知的獲得（詳見下例材料一）。優點是知識掌握得較扎實，不足的是學生的思維空間較小，往往按材料的暗示方向進行探索。另一類直達新知識本源的不暗示、富有想象空間的學習材料，其能使學生在探索中有充分的自由思維的時間與空間（詳見下例材料二）。學生學習主動性較高，思維的挑戰性更強，易激發學生的創新欲望，易出現富有創新性的探索結果。

例如，人教版五年級“三角形的面積”兩種不同的學習材料。

1.暗示性的材料。

材料一及簡要過程：

（2）將上圖沿一條對角線平均分成兩個三角形，求陰影部分的面積（如圖5）。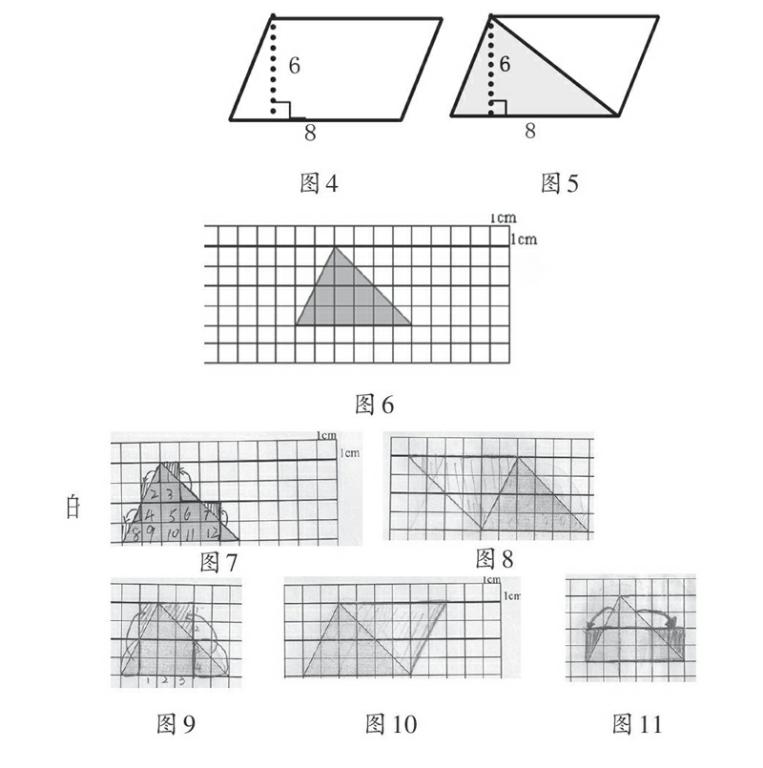

（3）對三角形面積計算方法進行猜測，再驗證。（過程略）

學生能證明三角形面積的計算，但都是用兩個全等三角形拼成平行四邊形的方法，結果較單一。

2.本源性的材料。

材料二及簡要過程：

（1）呈現如圖6材料，讓學生想辦法得到三角形的面積，再將自己的想法畫出來，使別人能一眼看出他們的想法。

（2）學生獨立畫圖，再展示思維過程，介紹自己的想法。具體如圖7～11所示。

（3）學生猜測三角形面積計算方式及驗證。（過程略）

從上例的探索過程與結果可以看出，我們把三角形的面積放到面積單位這一知識的源頭，打開了學生自由思維的空間，學生的探索過程不再單一，個性化想法非常豐富。

總之，在小學數學課堂上發展學生的創新意識是一個長期的、復雜的過程。學生創新意識的發展是一個由多種因素綜合起作用的整體性過程。既需要有自由探索的良好氛圍、充足時間及空間，還需要學生具有廣博的知識面，不畏艱險、勇于探索的精神，更需要學生具有善于提出問題、發現問題的能力。因此，培養學生的創新意識，我們還有許多問題要解決，還有許多做法有待研究。

參考文獻：

[1]曹培英.跨越斷層，走出誤區“數學課程標準”核心詞的實踐解讀之十——創新意識[M].上海：上海教育出版社，2015.

[2]陳選峰.基于“學”的課本材料有效的開發與實踐[J].教學月刊·小學版（數學），2014（6）.

（浙江省臨海市邵家渡中心校 317000）endprint