給予學生一個活動空間教師收獲幾多意外驚喜

付光華

摘要：通過對“30°角所對直角邊等于斜邊一半”的證明，為學生創設思維活動的空間，使其通過多種感官的協同作用實現多渠道獲得學習經驗。由此培養學生積極的學習興趣和嚴謹的探索精神。

關鍵詞：初中數學；教學過程；活動

中圖分類號：G633.64 文獻標識碼：A 文章編號：1009-010X（2017）20/23-0099-02

前蘇聯著名數學教育家斯托利亞爾認為：“數學教學是數學活動的教學，也是思維活動的教學。”教師要適時的給學生創設活動的空間，由學生通過動腦、動手、動口，充分調動多種感官協同活動，從多個渠道有效的獲得數學活動經驗。筆者依據“在直角三角形中，30。的角所對的直角邊等于斜邊的一半”定理證明的教學實例談一下自己的收獲與感悟，與同行交流。

問題背景：

冀教版教材八年級上冊《17.2直角三角形》在“做一做”欄目安排了“證明：在直角三角形中，30°的角所對的直角邊等于斜邊的一半”這一題目。教材并沒有給出證明方法，這就留給了教師和學生自由發揮的空間。在本課時中，教材在引出“直角三角形斜邊的中線等于斜邊的一半”這一定理時，采用了折紙的方法，筆者備課時，在折紙的過程中發現，能通過折疊含30°角的直角三角形紙片驗證“在直角三角形中，30°的角所對的直角邊等于斜邊的一半”這個定理，于是在在課上處理“做一做”這個環節時有了下面的問題。

問題呈現：

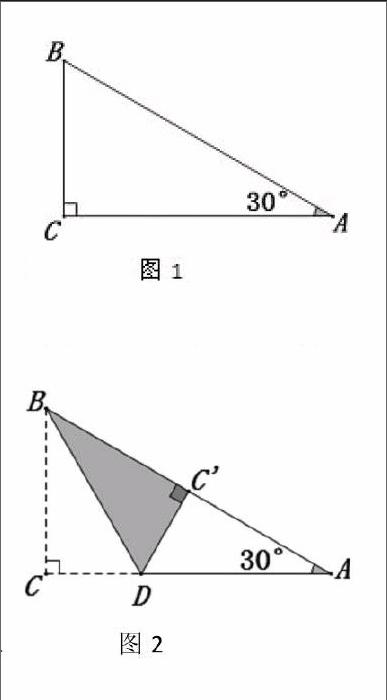
拿出事先準備好的含30°角的直角三角形紙片（如圖1），要求用折紙的方法驗證“在直角三角形中，30°的角所對的直角邊等于斜邊的一半”這一結論，有結果的先在小組內交流，然后到黑板前向全班同學分享成果。

活動實錄：

學生興趣盎然，通過動手、動腦、討論，很快就有小組到黑板前向全體同學展示本組的研究成果。

展示一：如圖2，將BC邊折疊至AB邊上，則LDBC=30°，因此LDBC=∠A，所以AD=BD，由“三線合一”可知：AC=BC，所以BC=AB.

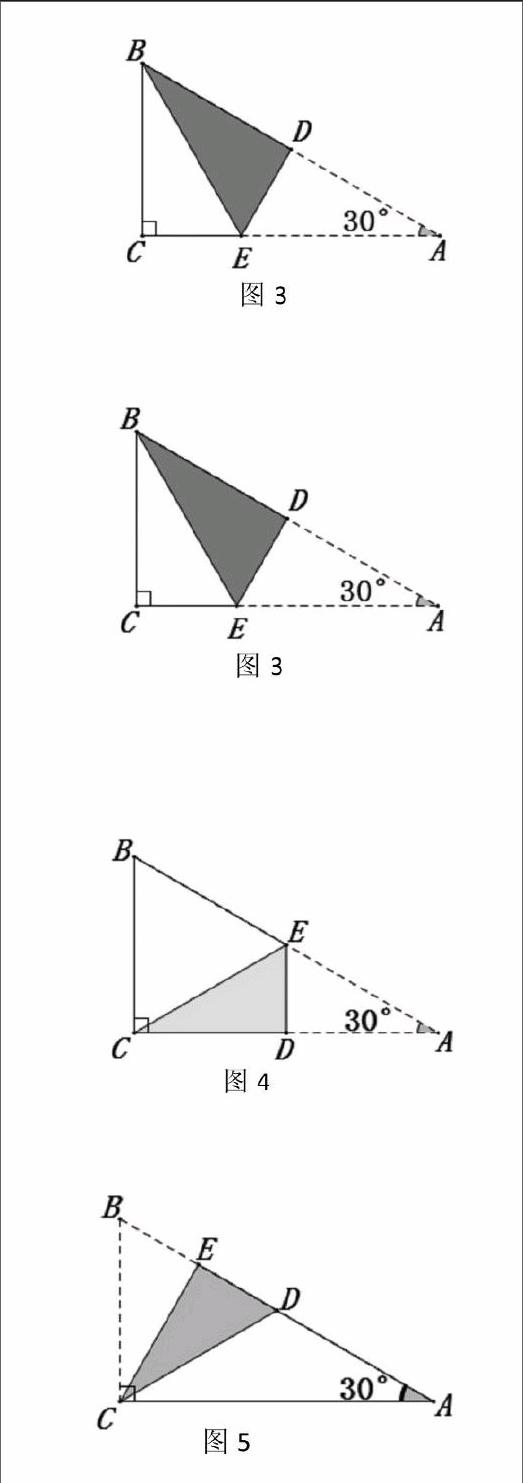
展示二：如圖3，把AB邊對折，則∠EBD=30°，∠BDE=90°，AD=BD.所以∠CBE=60°-30°=30°.利用“角角邊”可得ACBE≌ΔADBE，所以BC=BD，因此BC=1/2AB.

展示三：如圖4，把AC邊對折，則LECD=30°，AE=CE.所以∠BCE=90°-30°=60°，故有∠B=∠BCE=60°，所以可得ACBE為等邊三角形，因此BC=BE=CE=AE，至此得到BC=1/2AB.

意外驚喜：

以上三種折法是老師課前預設就此收兵，又有學生舉手示意要展示不同的折法。

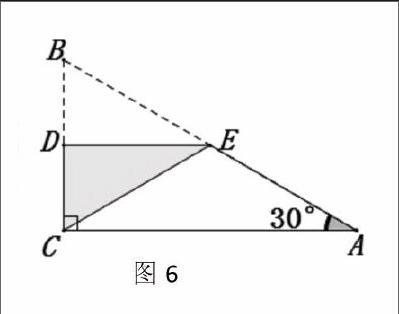
展示4：如圖5，將BC邊折疊至CD位置（當該同學把折疊好的紙片貼在黑板上時，老師仍不以為然，因為備課時教師做過這種折法的嘗試），然后這位同學又把翻折之前的部分用虛線畫了出來（前幾種折法不用此步），由此得∠B=∠BDC=60°，所以△ABCD是等邊三角形，即BC=BD=DC，所以LDCA=90°-60°=30°，因此∠A=LDCA，所以AD=CD，至此得到BC=1/2AB.

當這位同學展示完后，同學們自發的給出了掌聲（盡管此前成績平平，該同學對數學的學習態度變化不言而喻了）。

還沒等老師再發感慨呢，又有同學站了起來：“要是讓把沒折前的圖補出來，我還有不同的折法。”

展示5：如圖6，將BC邊對折，折痕為DE，則∠B=∠BCE=60°，所以BE=CE=BC，∠ECA=90°-60°=30°，所以CE=AE，至此得到BC=AB.

感悟與啟示：

第一，數學課堂教學活動要善于創設學生思維發展的空間，讓學生的思維之花絢麗綻放。課堂教學中，教師應該給學生思考的時間和空間，讓學生集中注意、用足力氣，運用已有的知識和生活經驗去認識未知，尋求解決問題的方法和策略。在本課中，筆者自認為給學生創設了思維發展的空間，而備課時自己都沒能將各種情況考慮周全，實屬教師之過，慶幸的是課堂中教師耐心的等待，沒有為了預設的教案而匆匆前行，課堂教學本應“以人為本”，學生是學習的主體。

第二，課堂教學教師要關注學生情緒，培養、呵護學生積極向上的心理情緒。以本節課為例，那位數學成績平平的學生要提出自己的思路時，如果教師以時間為理由，或硬生生的說：“我覺得再沒別的折法了，你的折法可能不對，下課你自己看看吧。”那么扼殺的不僅僅是一種解題方法、一個思維方式，也許是這個孩子最后一點學習數學的信心及積極思考的態度。

第三，教師要把課堂教學活動演化為學生體察良好情感的過程，獲得內驅力的過程。課堂上教師應該放手讓學生自己去思考探索，讓學生在挑戰學習困難、解決問題的過程中不斷找到新的方法，獲得新的發現，使能力得到提高、人格得到完善、精神得到發育和成長，這比知識本身更重要。

教師的課堂教學要著眼于學生終生發展，讓學生在愉悅的情緒中思考，在思考中成長，收獲并體驗成長的快樂，在成長中發育精神、形成能力，為一生奠基。

【責任編輯 馮夢陽】endprint