一脈相承解幾題 猶記去年三解法
——全國數學高考卷I理科第10題的研究與推廣

●洪劍林 (潮安區教育局教研室，廣東 潮州 515600)

一脈相承解幾題 猶記去年三解法
——全國數學高考卷I理科第10題的研究與推廣

●洪劍林 (潮安區教育局教研室，廣東 潮州 515600)

文章對2017年全國數學高考卷I理科第10題進行多解法研究、變式、評析、推廣及教學思考.該題與2016年卷Ⅰ理科第20題有相似的已知條件,一脈相承,可運用2016年的3種解法速解該題.

高考題;多解法;評析;推廣

1 試題的多種解法與評析

例1 已知F為拋物線C：y2=4x的焦點,過點F作兩條互相垂直的直線l1,l2,直線l1與C交于點A,B,直線l2與C交于點D,E,則|AB|+|DE|的最小值為

( )

A．16 B．14 C．12 D．10

(2017年全國數學高考卷Ⅰ理科試題第10題)

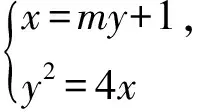
y2-4my-4=0,

從而

y1+y2=4m,

于是x1+x2=(my1+1)+(my2+1)=4m2+2,

因此

|AB|=x1+x2+2=4m2+4.

m2x2-(2m2+4)x+m2=0,

從而

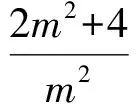
于是

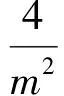
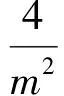
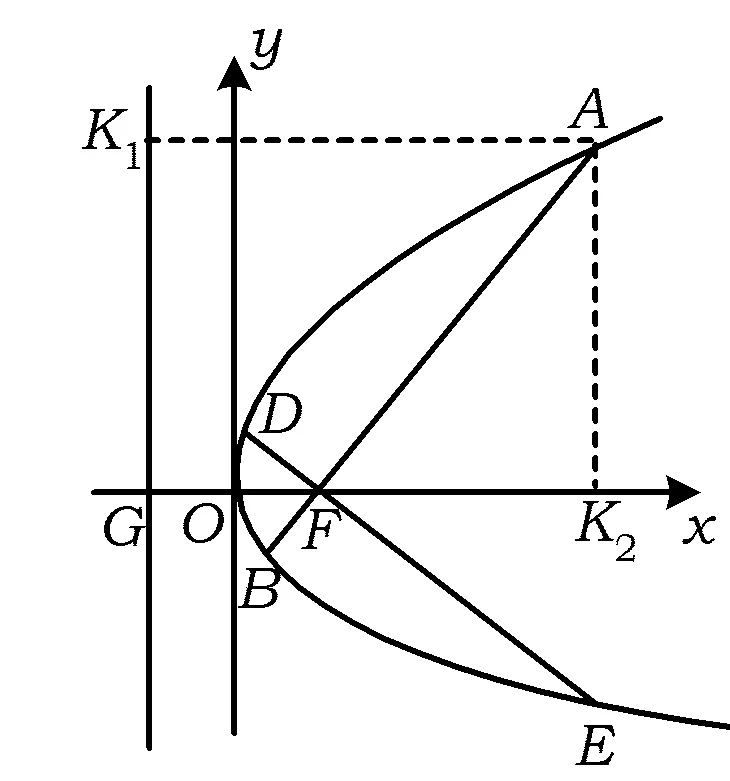
圖1

方法2 如圖1,直線GK1為準線,過點A作x軸和GK1的垂線,垂足為K2,K1.設l1的傾斜角為α(其中0<α<π),則|FA|= |AK1|=|GF|+|FK2|=

|GF|+|FA|cosα,

于是

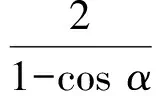
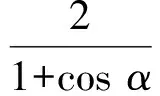
從而

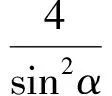
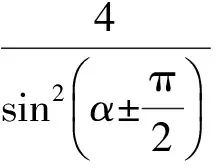
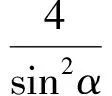
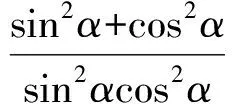
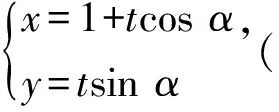
(sin2α)t2-(4cosα)t-4=0.

設方程的兩個解為t1,t2,則

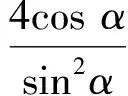
由參數t的幾何意義得

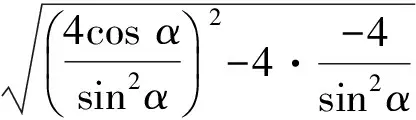
下同方法2.

2 試題點評

該題位于試卷的第10題,有一定難度,與2016年全國卷I理科數學解答題第20題有相似的已知條件——互相垂直的兩條直線且斜率都存在,可謂一脈相承.而文獻[1]中呈現了第20題的3種解法,記憶猶新,3種解題思想方法皆能速解2017年第10題.呈現成文,與同行交流.

方法1為代數方法,直線的方程不采用斜截式,而是設x=my+1，使弦長的計算簡潔得多,再用基本不等式求最值;方法2從幾何角度入手,利用拋物線的定義,結合解直角三角形,再用三角函數的有界求最小值;方法3運用直線的參數方程,利用參數t的幾何意義直接求解.解析幾何是用代數方法研究幾何問題,首先是幾何,“代數”只是我們解決幾何問題時用到的工具,由方法2可見“三角”也是不錯的工具,代數、幾何與三角渾然一體.

近年來全國卷試題中求四邊形面積取值范圍的試題還有很多,例1也可變式為求“四邊形ADBE面積的取值范圍”,即“求|AB|·|DE|的最大值”,與原題“求|AB|+|DE|的最小值”,考查的知識點同樣是韋達定理、基本不等式的運用,或是拋物線定義、三角的有界性,“現象”與“本質”皆是一脈相承.類似的題目還有:

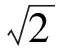
(2009年全國數學高考卷Ⅱ理科試題第16題)

答案：Smax=5.

例3 已知AC,BD為圓O:x2+y2=4的兩條互相垂直的弦,垂足為M(1,0),則|AC|+|BD|的最大(小)值為______.

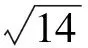
3 一般化推廣

推廣1 已知F為拋物線C：y2=2px的焦點,過點F作兩條互相垂直的直線l1,l2,直線l1與C交于點A,B,直線l2與C交于點D,E,則|AB|+|DE|的取值范圍為[8p,+∞).

注：推廣1的證明與例1基本一致,不再贅述.

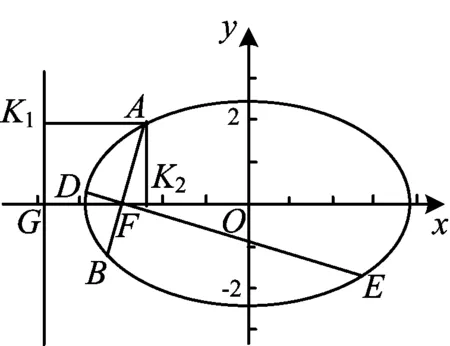
圖2

|FA|=e|AK1|=e(|GF|+|FK2|)=

即

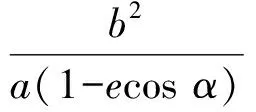
同理可得

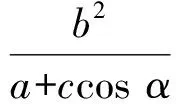
從而 |AB|= |FA|+|FB|=

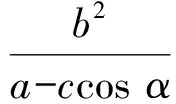
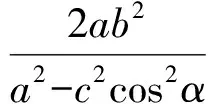
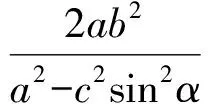
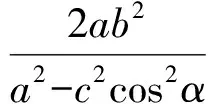
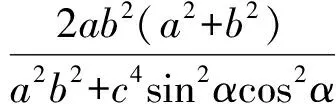
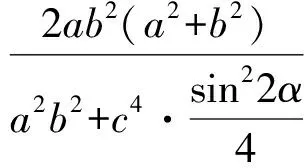
證法2[3]同證法1(或類比橢圓極坐標方程),且記左焦點到左準線的距離|GF|=p,則

|FA|=e|AK1|=e(|GF|+|FK2|)=

e·p+e|FA|cosα,

從而

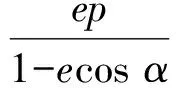
同理可得

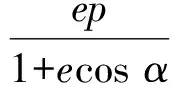
于是

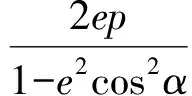
則

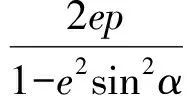
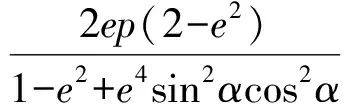
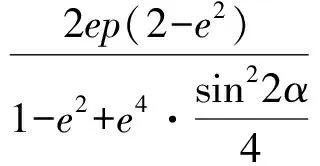
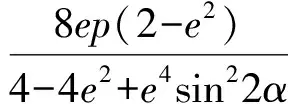
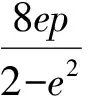
4 教學思考

數學教學中應當重視對題目的變式與拓展,抓住典型題目,一題多解,一題多變,“小題大做”也精彩.正如波利亞所說:“拿一個有意義且又不復雜的題目去幫助學生發掘問題各方面,使得通過這道題就好像通過一道門戶,把學生引入一個完整的領域.”

[1] 洪劍林.貌離神合 同源切線——全國數學高考Ⅰ卷理科第20題評析與思考[J].中學教研(數學)，2016(11):20-24.

[2] 洪劍林.《對一道高考題的一般化探究》的簡解與推廣[J].中學數學研究：高中版,2016,34(12):8-11.

[3] 中學數學室.高中數學[M].北京:人民教育出版社,2007.

2017-07-17

洪劍林(1976-)，男，廣東潮州人，中學高級教師.研究方向：數學教育.

O123.1

A

1003-6407(2017)09-41-03