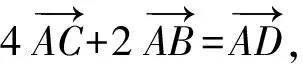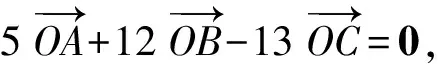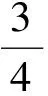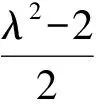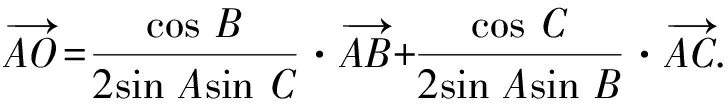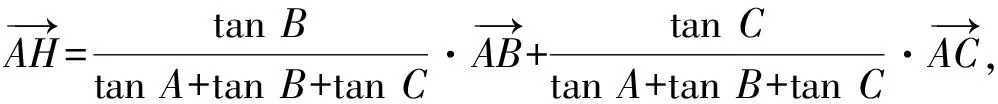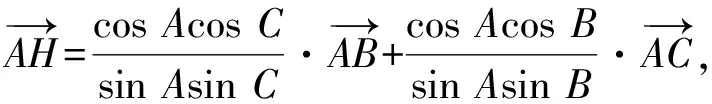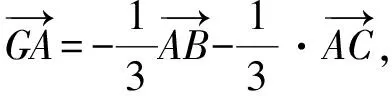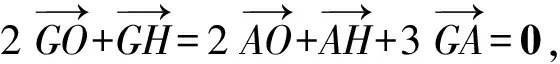不應排斥學科滲透問題的適度考查
●劉海濱 (鹽城中學,江蘇 鹽城 224005)
不應排斥學科滲透問題的適度考查
●劉海濱
(鹽城中學,江蘇 鹽城 224005)
拓展數學應用,讓學生學有用的數學,即學以致用,應是我們教學的一個重要目標.因此,高考應有正確的導向,不應固化考題,也不應排斥學科滲透問題的考查.只有多元化評價學生,考查學生的應用分析能力,這樣才能調動教師開展研究性活動課的積極性,才能拓展學生的數學應用能力,才能真正提高學生的數學素養.
不應排斥;學科滲透;適度考查
1 問題背景
前不久,筆者所在學校高三年級組織了一次檢測考試,數學試卷中有一道不同尋常的試題:
例1 如圖1,一根細繩穿過2個等高的定滑輪,且2端分別掛有3 N,2 N的重物.現在2個定滑輪之間的細繩上掛一個重量為mN的重物,恰好使整個系統處于平衡狀態,摩擦力忽略不計.
1)若細繩被重物拉成120°的夾角,求m的值;
2)求m的取值范圍.

圖1 圖2
該檢測題頗受爭議,筆者所在學校高三數學組的主流意見是:把物理學科中的力學問題,融入到數學應用題中,難度較大,學生難以理清有關力的一些數量關系,而且數學高考肯定不會考查有關物理方面的應用題,平時的數學練習還是應該盡量避免此類題目.
上述意見,筆者不能完全茍同,有下列疑問:數學測試真的不能考查有關物理方面的應用題嗎?我們的高考一定不允許學科滲透的考查嗎?帶著疑問,筆者做了一點思考,整理成文,與讀者交流、探討.
2 解題分析
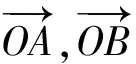
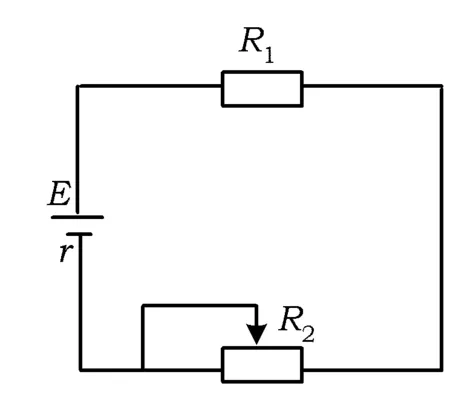
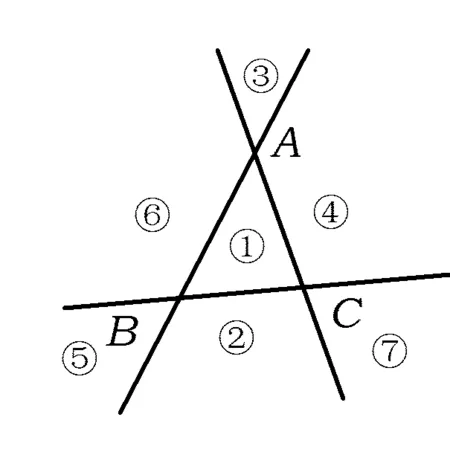
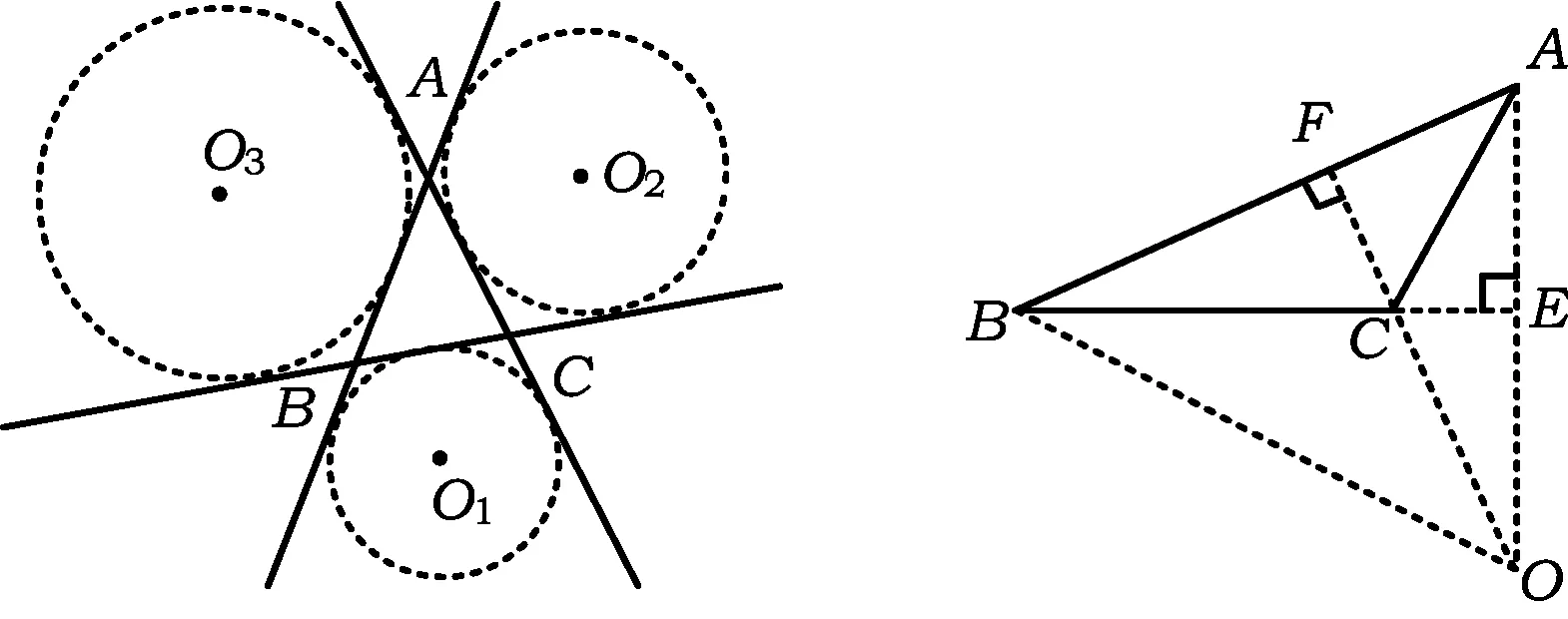
接下來就是圖形中邊角關系的研究.第1)小題中,120°的夾角即∠AOB,從而∠A=60°,在△AOC中運用余弦定理,即可求出m的值;對于第2)小題,很多學生在△AOC中運用三角形的三邊關系,迅速得到1 根據實際情況,重物將細繩向下拉,α,β應都是銳角,易知∠ACO=β.在△AOC中,由正弦定理可得 3sinα=2sinβ, 2個式子相加,化簡得 m=3cosα+2cosβ. 結合上述正弦等式,消去α,可得 可能有人認為:2次運用余弦定理的運算處理有點靈活,學生不易過關.確實如此,但這類問題在物理學科中,通常是由水平方向的合力為0,即由正弦定理可得3sinα=2sinβ;以及豎直方向的合力為0,從而直接得出m=3cosα+2cosβ.如此,很容易想到消角,轉化為m關于β的函數. 對于例1,也許有人會說,它是一道物理題,不是數學題.說例1是物理題,肯定沒有錯,它就是日常生活中的滑輪問題,確實是物理方面的問題.但說它不是數學題,值得商榷! 要用一個標準嚴格界定一個問題是不是數學題,不是一件容易的事,但我們可以粗略地把數學題分為2大類:一類是純粹的數學問題,以研究空間形式和數量關系為主(百度百科釋義);另一類是數學應用問題,主要是運用數學知識解決生產、生活中的實際問題,即我們常講的數學建模.據此,我們可以認為例1是數學應用題,只不過它是與力有關的問題,雖然是物理問題,但這并不妨礙它作為數學題.其實,數學與物理本來就是一家,沒有數學理論知識作支撐,能研究物理問題嗎?比如向量的引入,就源自于力學[1].數學就是解決實際問題(包括物理問題)的一個工具,從某種程度上講,物理問題就是一類特殊的數學應用題. 回顧上述例1的解題過程,只是用了一點力的合成知識而已,而且這與數學中的向量加法是一致的,完成求解的主體過程是三角函數等數學知識,因此其作為數學題,不為過.若對于某一個問題的解決,所需物理知識的比重很大,遠遠多于數學知識,則把它作為數學題,就有點不合適了. 圖3 翻開蘇教版高中教材《數學(必修4)》,筆者發現:在“向量的應用”這節內容中,上述例1就是由課本題改編而來的(是在課本題的基礎上,增加了第1)小題).并且類似于例1這樣的“力與運動”方面的題目還有6道,筆者在此不一一例舉[1].另外,在《數學(必修5)》“基本不等式”這節內容中,也有2道有關物理方面的題目:一道是杠桿問題[2],另一道是電學問題(即以下例2). 例2 如圖3,電路中電源的電動勢為E,內電阻為r,R1為固定電阻,R2為一個滑動變阻器.R2調至何值時,其消耗的電功率P最大?最大電功率是多少(其中P=I2R)? 此外,在《數學(必修1)》“函數模型及其應用”一節中,有物理冷卻問題;在《數學(選修2-2)》“導數及其應用”一章中,有不少物理方面的問題.教材上這么多物理方面的應用問題說明:應充分關注數學應用教學,不應忽視數學知識在物理方面的應用,不應排斥學科滲透問題的考查. 4.1 不應固化考題 對于高考,筆者總是覺得過于保守了,試卷的固化太嚴重.高考之前給每個學生發《考試說明》,而根據《考試說明》命制的試卷,教師基本上都能估計到“什么題號對應什么題型,是什么難度”. 這樣的試卷,對高中教學的影響比較大,不考的不教、必考的重點,反復講反復練,課堂目標明確、重點突出,其實就是應試教學!教材上的閱讀材料,沒空讀;教材上的探究問題,沒空探.這樣的教學,有點像工廠生成模具,所教出來的學生,都限制在一定的知識水平內,不能使學生學有所長,學生的個性化發展很差. 筆者認為:我們的高考不應固化考題,為什么要限制考題數量?完全可以根據試題難度調整數量,保證大多數學生有思考完成的時間即可.為什么要規定重要考點?文獻[3]指出:高考應有正確的導向,有必要增加研究型試題,多元化評價學生,考查學生的研究分析能力,這樣才能真正改變廣大教師的守舊認識,調動教師積極開展研究性活動課,拓展學生的知識面,提高學生深入研究問題的能力,為教育創新起引領作用.總之,不限制考試思路,才能打開教學思路,才能讓教師各盡其才,教出有深度和廣度的學生. 4.2 應拓展數學應用 在平日的教學中,教師之間也常交流數學學習的作用,普遍認為:數學的學習能使人變得更聰明,它能鍛煉人的思維分析能力,對今后的工作生活有著潛移默化的影響,而且數學是將來從事理工科工作人群的必要基礎知識,是高端科研的必要知識. 筆者認為:中學數學教學應拓展數學應用,要讓學生學有用的數學,要讓我們的日常生活充滿數學.當這些學生步入社會,即使不從事理工科的工作研究,他們也感到數學是有用的,并能把數學知識用到工作、生活中,這樣我們的數學學習才更有意義,也才能讓全社會都認同數學學習. 學習數學的目的是要讓學生學有所用,解決生活中的實際問題,而不要刻意加大難度,反而有些生活問題,適當簡化命題,倒是很有必要.沒有必要排斥學科滲透問題的應用,而應該擴充數學應用的范圍,加大數學應用題的考查,從而真正提高教師的應用教學意識,切實提高學生的數學建模能力. 高考命題要有原則,原則是要有正確的教學導向作用,要引導教師遵守教學理念,發揮自身所長,不僅要教給學生課本知識,更要教出自己的理解與觀點,帶領學生開展研究性學習活動,讓學生學會思考,學會獨立解決問題. [1] 單墫.普通高中課程標準實驗教科書·數學(必修4)[M].南京:江蘇教育出版社,2012. [2] 單墫.普通高中課程標準實驗教科書·數學(必修5)[M].南京:江蘇教育出版社,2012. [3] 崔志榮.高考數學應適當增加“研究型試題”的分析[J].數學通訊,2017(2):8-13. 若按順時針排列,則 圖1 如圖1所示,將三角形所在平面分成7個區域,文獻[1]和文獻[2]已經證明了點O在△ABC內部(即區域①)的情形. 1)若點O在區域②內,則τ(A,BC,O)=-1,τ(B,CA,O)=-1,τ(C,AB,O)=-1,此時點O,B,C按順時針排列,點O,C,A和點O,A,B按逆時針排列,從而 2)若點O在線段BC上(不含端點),則點O,B,C共線,進一步有x2y3=x3y2.此時,τ(A,BC,O)=0,τ(B,CA,O)=1,τ(C,AB,O)=1,點O,C,A和點O,A,B按順時針排列,從而 同理可得 我們還可以把定理1闡述如下: 根據前面的定理,結合三角形“五心”的幾何特征,可以得出一些等式,根據文獻[1]的結論,下面的各個推論也只需對于鈍角三角形的情形作出證明. 圖2 圖3 推論2 如圖2,點O1,O2,O3是△ABC的旁心,則 證明 若△ABC為鈍角三角形(其中∠C為鈍角),則垂心O在三角形的外部(如圖3),根據定理1可得 因為 即 S△OBC∶S△OCA∶S△OAB=tanA∶tanB∶(-tanC), 所以 圖4 證明 若△ABC為鈍角三角形(其中∠C為鈍角),則外心O在三角形的外部(如圖4),根據定理1可得 因為S△OBC=2R2sin∠BOC,S△OCA=2R2sin∠COA,S△OAB=2R2sin∠AOB,所以 又∠BOC=2A,∠COA=2B,∠AOB=2∠D=2(π-∠C),故 從上可以看出,三角形外心、內心、垂心的向量表示形式都與三角函數相關,且銳角三角形和鈍角三角形的情形完全一致,簡潔實用,可謂珠聯璧合,給人以美的享受!如果改用三角形的邊或面積來表示,則需要分情況討論,達不到這個效果. (2014年浙江省高中數學競賽試題第12題) (2016年全國高中數學聯賽山東賽區預賽試題第5題) 以上3個例題都涉及到點在三角形外部的情形. sinA∶sinB∶sinC=2∶2∶1, tanA∶tanB∶tanC=1∶2∶3. 例6 (歐拉線)設△ABC的外心為O,重心為G,垂心為H,則點O,G,H共線. 證明 對于直角三角形,結論是顯然的.對于非直角三角形,由推論4可得 故 即點O,G,H共線. 以上3個例題利用三角形“五心”統一向量表示形式,解題過程十分簡單. 三角形的“五心”既有統一的向量表示形式,又有關乎三角形各角的等量關系,易于記憶,方便使用,在解決此類問題時還可以達到“秒殺”的效果. 參 考 文 獻 [1] 朱慶華.面積法求三角形的五心的向量表示的同一形式[J].數學通訊,2010(5):40-41. [2] 關麗娜,鐘德光.三角形“五心”向量形式的一個簡證及應用[J].中學教研(數學),2017(1):31-34. [3] 克萊因.高觀點下的初等數學·幾何[M].上海:復旦大學出版社,2007. 2017-04-24 劉海濱(1969-),男,江蘇鹽城人,中學高級教師.研究方向:數學教育. O12 A 1003-6407(2017)09-32-03
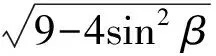

3 題類探討
4 學以致用

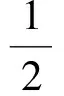
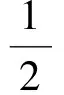
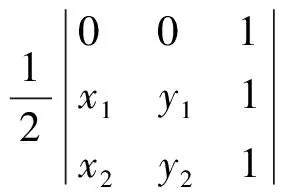
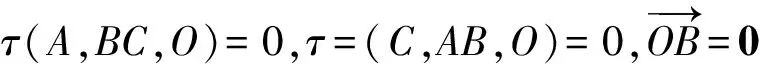
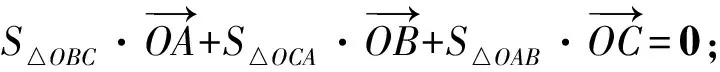
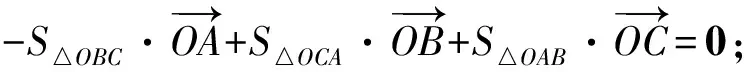
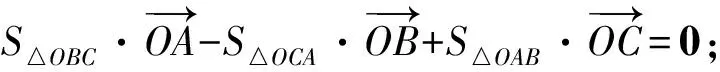
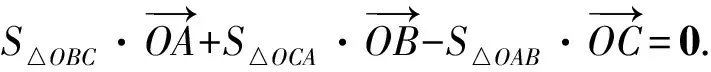
2 三角形的“五心”
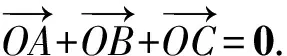
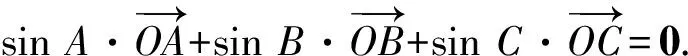
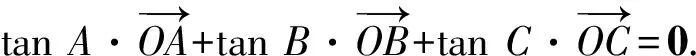
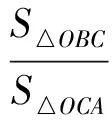

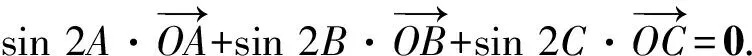
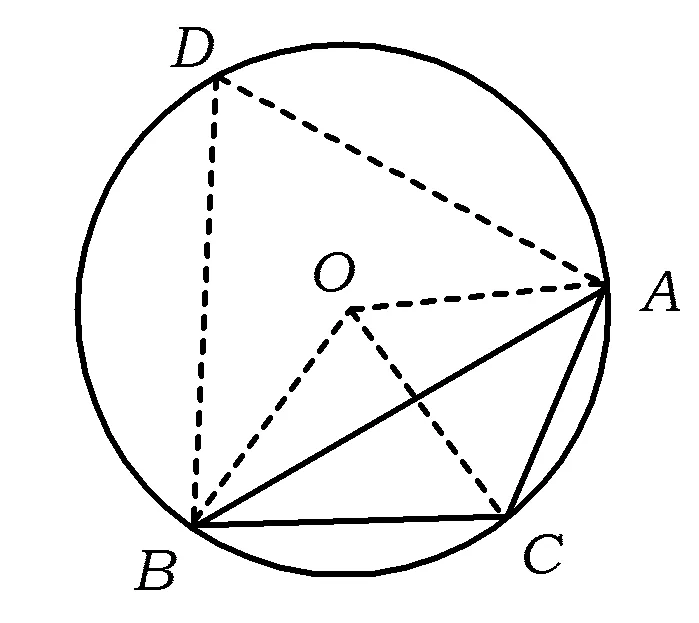

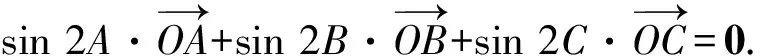
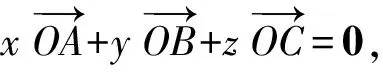
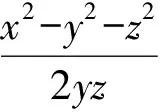
3 解題中的應用