不忘初心 方得始終
——基于2017年浙江省數學高考第21題

●金燦芳 (蕭山中學,浙江 蕭山 311200)

不忘初心 方得始終
——基于2017年浙江省數學高考第21題

●金燦芳
(蕭山中學,浙江 蕭山 311200)

解題中會有困惑與停頓，但解題中更有收獲與快樂.文章從代數、幾何、向量這3個方面探討了2017年浙江省數學高考第21題的解法，多角度揭示了此題的本質，并由此提出了應對高考復習的教學建議.

代數；向量；解析幾何

1 考題再現

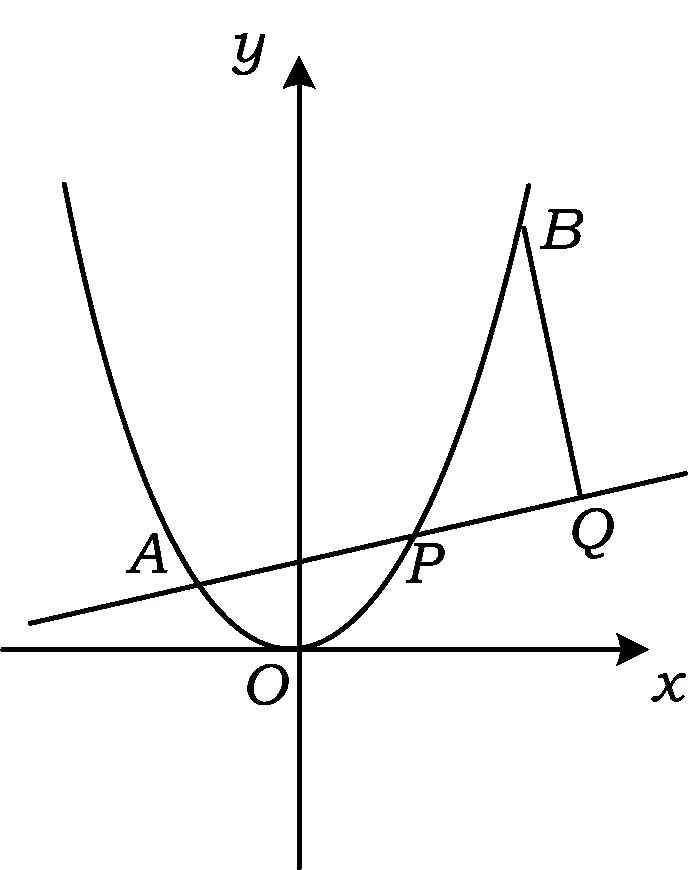
圖1

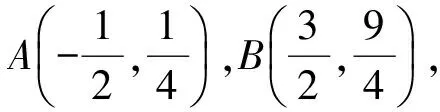
1)求直線AP斜率的取值范圍；

2)求|PA|·|PQ|的最大值.

(2017年浙江省數學高考試題第21題)

此題作為文理合卷后首年的圓錐曲線大題，載體是拋物線與直線，兼具常規與新穎的特點.題目主要考查兩點間的斜率公式、直線與圓錐曲線相交的弦長公式，題型中規中矩.本題可以通過代數、幾何、向量等多種途徑入手解答，不僅考查了學生的代數運算功底，也考查了學生從問題本質出發對問題的轉化和化歸能力，對學生有一定的挑戰.

2 解法探究

視角1 代數的視角

1)解 設P(t,t2)，則

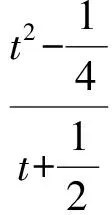
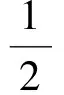
2)解法1 因為直線PA的方程為

(1)

而BQ⊥AQ,所以直線BQ的方程為

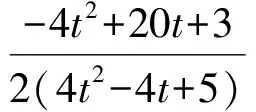
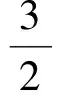
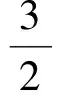
f′(t)=-4t3+3t+1=-(t-1)(2t+1)2,

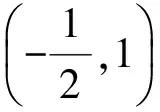
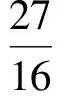
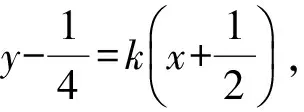
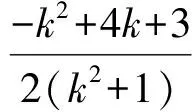
直線AQ與拋物線x2=y聯立得

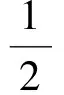
可得

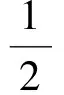
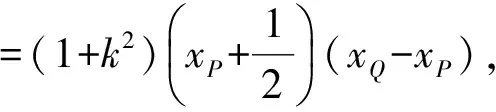
將xQ，xP代入，得

|PA|·|PQ|=(1+k3)(1-k).

令f(k)=(1+k)3(1-k)，則

f′(k)=(1+k)2(2-4k)，

從而

點評 第1)小題考查的是兩點連線的斜率公式，直接設點的坐標代入，利用拋物線的標準方程進行消元即可.第2)小題的解決辦法從代數的角度很直觀，求出點Q的坐標，這也是大多數學生首先能想到的，但只有少部分學生按照這個思路能做到底，最主要的原因是運算遇阻.無論是解法1(設點P的坐標)還是解法2(設直線AQ的方程)都需要聯立直線方程，求出點Q的坐標，這是代數方法的第一個難點.第二個難點是要用求導的方法求最值，解法2中f(k)的導函數較容易求得.在直線與圓錐曲線的位置關系中，代數法的繁瑣不可避免，因此打下扎實的運算功底很重要，教師要注意培養學生優化運算的能力，比如本題能否避開求點Q的坐標.

視角2 幾何的視角

1)解 因為y′=2x，則在點A處的切線方程的斜率為-1，而kAB=1,所以kAP∈(-1,1).

2)解法3 設P(t,t2)，由代數法知

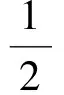
則

直線BQ的方程為

從而點P到BQ的距離

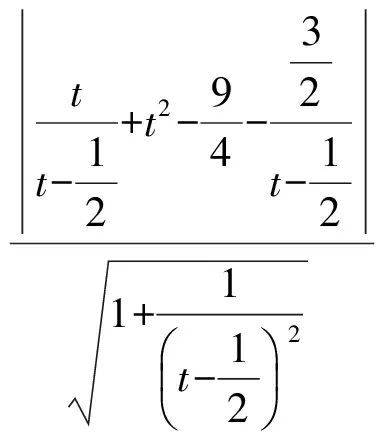
于是|AP|· |PQ|=d·|AP|=

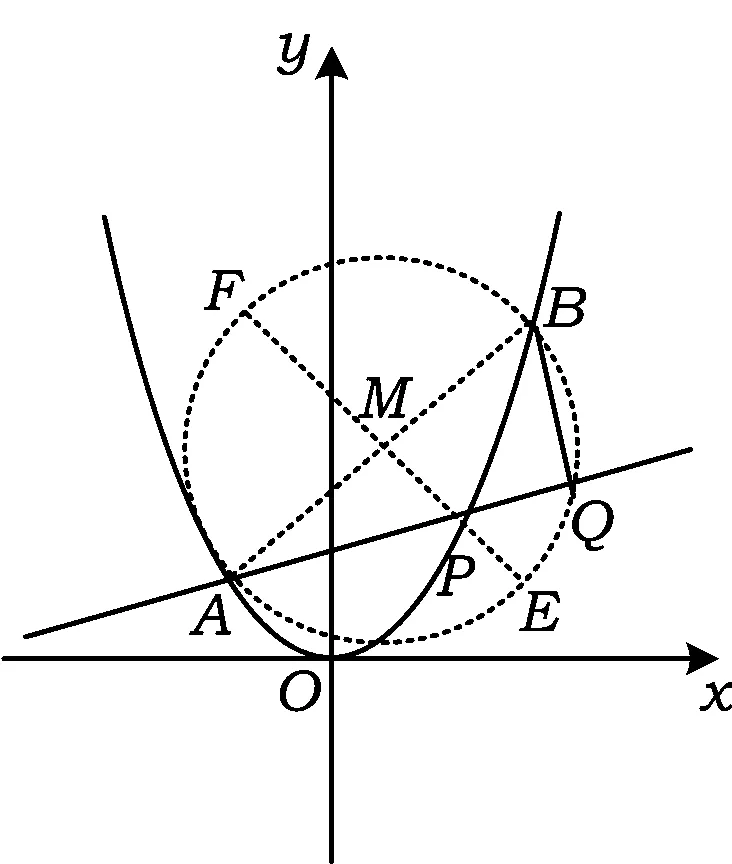
圖2

以下同解法1.

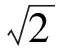
|AP|·|PQ|= |PE|·|PF|=

(R-|PM|)(R+|PM|)=

R2-PM2=2-PM2,

要求|AP|·|PQ|的最大值，即求PM2的最小值.設P(t,t2)，則

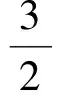
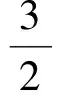
g′(t)=4t3-3t-1=(t-1)(2t+1)2,

從而

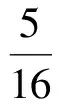
于是

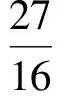
點評 解法3利用AQ⊥BQ這個條件，將|PQ|表示為點P到直線BQ的距離，避免了代數方法中最繁瑣的點Q坐標的運算，當然還可以利用勾股定理來得到|PQ|，即轉化為求點B到直線AQ的距離.解法4利用圓冪定理，因為點Q在以AB為直徑的圓上，所以

|AP|·|PQ|=|EP|·|FP|，

即轉化為求|PM|的最值；求|PM|2的最值采用兩點間的距離公式來表達，不僅避免了求點Q的坐標，還避免了點到直線的距離公式.幾何方法相對快速地獲得了|AP|·|PQ|所對應的解析式，實現了運算上的優化，后面求導的部分與代數法一致.

視角3 向量的視角

向量的方法主要針對第2)小題.

解法5 設P(t,t2)，則

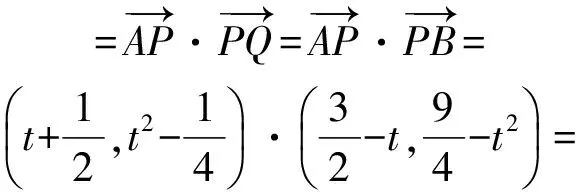
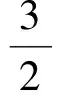
以下同解法1

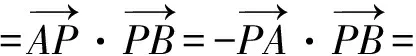
-(PM2-AM2)=-(PM2-2),

以下同解法4.

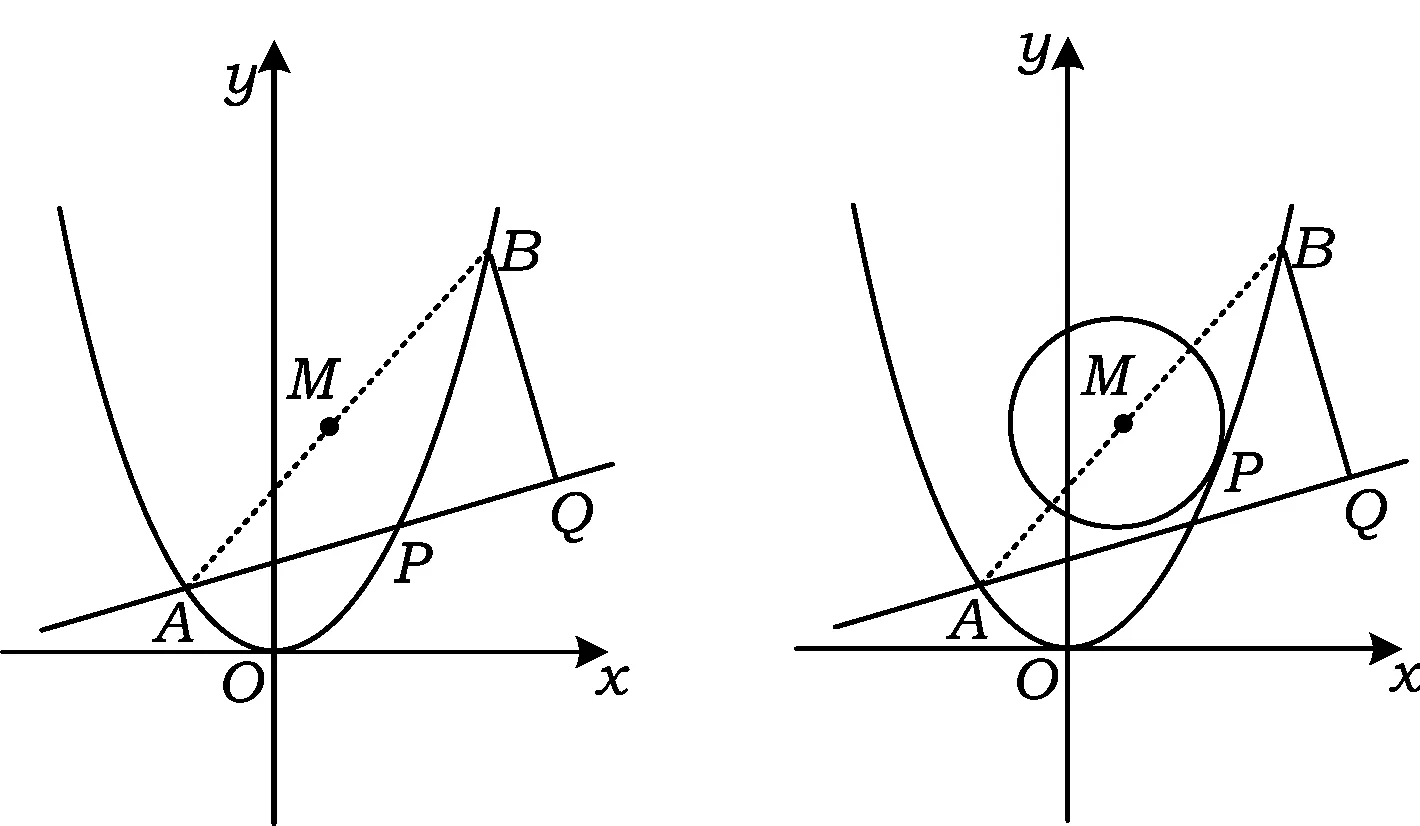
圖3 圖4

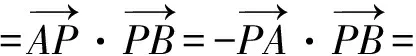
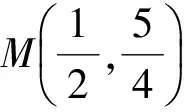
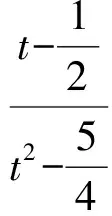
拋物線在點P處的切線斜率為k2=2t，從而

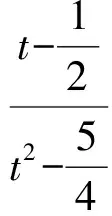
即

4t3-3t-1=0,

解得t=1，故

點評 向量法是本題的亮點，核心就是利用向量的幾何意義得到

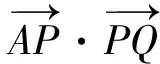
之后的處理又可以分成兩種情況.解法5直接用向量的坐標表示來表達數量積，簡潔明了地得到解析式.解法6和解法7用極化恒等式將最值轉化為求|PM|的最值，|PM|的最值可以用兩點間的距離(同視角2)，也可以用幾何上的特殊情況來解決，因為|PM|取最小值時就是以M為圓心的圓與拋物線相切，所以解法7中利用圓與拋物線相切的公切線方程很快地得到了切點坐標.

3 解后反思

3.1 夯實基礎，提升能力

對于圓錐曲線大題，有句老話：“圓錐曲線無難題”，但是也有一句很諷刺的話：“有些高中生到畢業了也沒能完整地做完一道大題.”圓錐曲線的大題以常規題居多，無論是求最值還是證明定值，總少不了聯立方程、韋達定理、弦長公式等常規手段.本題也不例外，可以用韋達定理表示點P的坐標，用弦長公式來表示|PA|·|PQ|，這樣看來沒有難點，但是這些常規步驟的運算量都不小.很多學生就敗在運算上——聯立、判別式等等都容易求錯，只要有一個小地方求錯，后面的化簡就不成功了.還有一些學生運算遇阻時常猜測答案，甚至直接放棄，認為算算的東西總會的，這是學習上的“紙上談兵”，一到真槍實戰的考場，狐貍尾巴就露出來了.因此，教師要不斷地提醒學生打磨自己的運算功底，越不順利越要找到原因，每做一題都要爭取做到底，找到自己算不對的地方，吸取失敗的教訓，積累經驗，只有這樣才能提高自己的運算能力.

3.2 重視概念，關注本質

概念是最容易被學生忽視的，因為學生認為它沒什么內容，太簡單了.其實很多題目歸根究底就是在考概念和定義.比如向量數量積的定義，考生幾乎都知道向量數量積的幾何意義，大部分學生也能答上來，并且教科書上講投影這塊內容的圖和本題的圖非常相似，但是在考試中，只有很少的學生能把結果轉化為數量積，歸根結底還是對概念的本質沒有研究透，挖得不夠深.教師首先要重視概念，重視概念本質的挖掘，在平時的講解中要滲透，還要引導學生梳理概念，再結合已經做過的題打磨概念，做到“以不變應萬變”[1-2].

3.3 研究專題，優化解題

英語中的單詞是有詞根的，一個詞根能關聯一連串的單詞，數學也是一樣，我們會有一些母題，也可以稱之為題根.那么在高考復習時，教師按專題整理或引導學生整理就尤為重要.不僅如此，我們還可以把題根做多角度的延伸，或通過某條思路串起看似不同專題的題，這在某種程度上也可以培養學生轉化與劃歸的能力.具備這樣的能力，在不經意間就優化了解題過程.眾所周知，運算是圓錐曲線問題的一個難點，可以把優化運算作為一條線索來整理，比如消哪個元，計算三角形或四邊形的面積時要找到最簡單的表示方法，計算距離時要嘗試一下弦長公式，處理定點問題時可以先設點再證明，能不能用幾何或向量思路來轉化等等[3].

2017年的高考已經結束，有些高考題平淡中透著驚喜，就看學生們能否正確把握，用心地打磨運算功底，用心地挖掘概念本質，用心地研究專題分類，正所謂“不忘初心，方得始終”.

[1] 李學軍，曲文瑞.大音希聲 大象無形——基于2016年浙江省數學高考理科第15題[J].中學教研(數學),2016(12):43-46.

[2] 曹鳳山.數學教學 把根留住——2015年浙江省數學高考試題解讀[J].中學教研(數學)，2015(8)：1-4.

[3] 高考數學研究組.浙江高考數學2004一路走來[M].杭州：浙江大學出版社，2016.

2017-07-20

金燦芳(1982-),女,浙江蕭山人,中學一級教師.研究方向:數學教育.

O123.1

A

1003-6407(2017)09-38-04