都是定義惹的禍
——一道易錯題的錯因分析和教學建議

●孫 鋆 (寧波市第二中學,浙江 寧波 315010)

都是定義惹的禍
——一道易錯題的錯因分析和教學建議

●孫 鋆
(寧波市第二中學,浙江 寧波 315010)

文章從一道函數題常見的錯誤出發，尋找錯誤背后的主因，通過對復合函數定義的合理選取，消除學生在理解上的障礙點，并通過對復合函數定義的縱向梳理，進一步提出切實可行的教學建議.

函數值域;錯因分析;復合函數定義

1 問題緣起

三年輪回，筆者轉眼又任教于高一數學，而每當講授到“對數函數”之后，學生在函數問題上的錯誤頻發，其中有這樣一個經典問題，常常講評，但錯誤率還是極高，現呈現如下.

例1 若函數f(x)=ln(x2+mx+1)的值域為R，求實數m的取值范圍.

錯誤解法 設u=x2+mx+1，由題意知其相應的判別式為Δ=m2-4<0，即m∈(-2,2).

眾所周知,這樣的結果是錯誤的.如取m=0，則函數f(x)=ln(x2+1)的值域是[0,+∞),顯然與條件矛盾，而這樣的解法普遍存在于學生中.為了糾正學生的錯誤,筆者給出正確的想法:易知y=lgu在u∈(0,+∞)上單調遞增且值域為R,欲使原函數值域為R，可設u=x2+mx+1值域為U，則必有(0,+∞)?U，因此相應的判別式Δ=m2-4≥0，即m∈(-∞,-2]∪[2,+∞).而令筆者驚奇的是講評成效甚微，基礎中等和偏下的學生還是做錯.

2 錯因分析

筆者向學生了解他們的解題想法，大多數學生考慮到對數的真數必須大于0，又必須滿足集合為R，因此想到Δ<0.不難發現學生將例1和“若函數f(x)=lg(x2+mx+1)的定義域為R，求實數m的取值范圍”混為一談.是學生真的教不會還是學生真的太“笨”而導致屢教不改嗎？答案是否定的，其實問題出在教師的教學之中.

2.1 定義“惹禍”

復合函數作為初等數學重要的函數構成方式，盡管現行的高中教材并未給出其定義，但一般教師都會作為補充內容向學生講授，而上述例1錯誤解法的原因正好來自于復合函數的定義方式.

文獻[1]指出復合函數定義有兩大類型8種定義格式，現摘錄其中具有代表性的兩種定義.1)定義1：設函數y=f(u)的定義域為D1，函數u=g(x)在D上有定義，且g(D)?D1，則由下式確定的函數y=f(g(x))稱為由函數y=f(u)和函數u=g(x)構成的復合函數；2)定義2：如果y是u的函數y=f(u)，u∈U，而u又是x的函數u=g(x)，x∈X且D={x|g(x)∈U,x∈X}≠φ，則函數y=f(g(x))稱為由函數y=f(u)和函數u=g(x)構成的復合函數.

2.2 禍害橫流

復合函數作為重要的函數類型常常出現在不同類型的考試中，但實際上很多問題的編制是存在漏洞甚至是錯誤的.文獻[2]主要列舉了8種與復合函數相關的錯誤類型，如：

例2 函數f(2x)的定義域為[-1,1],求f(x)的定義域.

錯誤解法 令g(x)=2x，由f(2x)的定義域為[-1,1],得

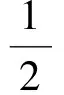
即

此時函數

定理1 若函數f(g(x))和g(x)都有已知的顯式表達式，且Rg=Df，則f(x)的解析式被唯一確定.

定理2 若函數f(g(x))和g(x)都有已知的顯式表達式，且Rg=R，則f(x)的解析式被唯一確定.

事實上2個定理都在強調外函數定義域的確定性.上述由于復合函數中外函數定義域的不確定性導致了諸多錯誤，這樣的錯誤仍然出現在部分教輔資料之中.

2.3 厘清認知

實際上關于此類問題的爭論經歷了大約30余年，為了徹底厘清對復合函數定義中相關問題的認識，文獻[4]對多年來的相關文獻進行了梳理和綜述，并且旗幟鮮明地肯定定義2的正確性，在此筆者引入其中幾個爭論階段的典型觀點.

事實上此種定義符合復合函數定義的科學性.進一步,若記U={u|u=g(x),x∈E}及U*={u|u=g(x),x∈E*}，得到的結論是：若已知復合函數f(g(x))和內函數g(x),而外函數未知，則只可求得E,U,E*,U*，對應外函數的定義域D僅能得到U*?D且U*?U.若CUU*≠φ，則外函數f(x)必在CUU*上無定義,即D∩CUU*=φ，一般而言較難確定f(x)的定義域D，由此外函數f(x)也不能確定，只能得到在U*上的表達式.文獻[4]特別指出，遺憾的是這一正確的結論并未被廣大數學教育工作者所熟知,從而導致再次出現“錯例—辨析—錯例—再辨析”的現象.

由此不難得出例1的正確解法，欲使f(x)=ln(x2+mx+1)的值域為R，只需u=x2+mx+1的值域U?(0,+∞)=U*，而學生擔心的正是外函數在集合CUU*上無定義而導致無法復合的情況.

3 教學建議

通過查閱文獻資料,筆者不禁感嘆對于復合函數問題的爭論如此熱烈，多年來自己對很多問題的認識仍存在錯誤理解和片面認識.如何盡可能地避免類似的問題再次發生,筆者提出以下建議：

3.1 建議于教材編寫者

由于高中階段復合函數存在的普遍性和重要性，盡管其定義較為抽象，但是幾乎所有高中數學教師都會作為補充內容進行教學.為了避免對上述復合函數相關問題進行無謂的爭論，建議將此定義編入教材并進行權威發布以正視聽.倘若出于課時限制的因素，則可以將此內容作為拓展知識放置到課后的閱讀材料.

3.2 建議于教輔編寫者翻開各種形形色色的教輔資料，必然會找到相關爭論的復合函數定義域或解析式等問題，教輔資料的編寫教師應當具有科學的態度和高度的責任感,慎重選擇相關復合函數問題的類型，防止將一些錯題放入相應的資料中，務必提高資料的質量.

3.3 建議于高中數學教師

教師對一些習以為常的數學問題的解法或結論應保持一種科學的態度、反思的習慣和批判質疑的精神.教師要重視學生中出現的一些易錯題，原因或許不僅僅是學生能力的問題，也可能是教師講授的問題(包括知識或方法等).我國著名的數學教育家張奠宙曾說：數學的核心素養就是“真、善、美”三個維度，即理解理性數學文明的文化價值，體會數學真理的嚴謹性和精確性；具備用數學思想方法分析和解決實際問題的能力；能夠欣賞數學智慧之美.

作為數學教師,要以身示范并積極投身到當下新的課程改革實踐中，努力培養學生對數學“真、善、美”的認識和感悟.

[1] 趙光耀.復合函數定義形式的討論[J].北京工業職業技術學院學報，2004,3(1)：85-88.

[2] 張金良.理清復合函數概念 突破外函數求解疑難[J].中學教研(數學)，2005(8)：43-46.

[3] 陳鴻斌.關于復合函數問題的研究[J].數學學習與研究，2011(3)：117.

[4] 本刊編輯部.爭論早就有結論 莫讓錯例長期留——關于復合函數反編制問題的部分爭鳴資料[J].數學教學研究，2014(7)：2-6.

2017-05-26

孫 鋆(1979-)，男，浙江寧波人，中學高級教師.研究方向：數學教育.

O122.1

A

1003-6407(2017)09-07-03