優化初三數學復習課教學的實踐與思考

●童桂恒 (金華市第四中學，浙江 金華 321000)

優化初三數學復習課教學的實踐與思考

●童桂恒
(金華市第四中學，浙江 金華 321000)

數學復習課是數學教學中一類基本的也是十分重要的課型.一堂高效的復習課不僅有利于學生掌握基礎知識、基本技能、基本思想和基本活動經驗，而且有利于提高學生的數學素養.反思當前數學復習教學中存在的一些低效乃至無效的教學行為，復習課要從“選、講、練”這3個維度去平衡把握，通過“精選問題、分層施教、變式拓展”等方法，真正實現減負增效之目的.

復習教學；變式教學；分層教學；教學反思

數學復習課是數學教學中一類基本的也是十分重要的課型，要從“選、講、練”這3個維度去平衡把握，要關注數學思維方法的訓練，掌握數學的解題方法，同時也要注意糾正兩種傾向：一是要避免“重思路引導，輕有效的鞏固訓練”；二是要避免“重策略探討，輕必要的糾錯過關”．一節課的內容不要貪多，復習時既要重視每年必考的重點內容和相關典型問題，強化主干知識的訓練[1]，又要把握好重點內容與雙基內容的復習時間與力度，反復訓練，力求全面掌握，教后還要有跟進的題目加以鞏固.

1 精選例題，方法變式

一道典型的例題，不僅具有鞏固所學知識的作用，更有優化思維品質的功能.因此，在教學中教師要引導學生開展方法變式，在掌握通性通法的基礎上，深刻分析命題條件的特殊性，讓學生在問題的解決過程中對命題條件有本質的認識，從而達到會解一類題目的目的．

圖1

例1[2]如圖1所示，在△ABC中，AB=AC，P為BC上的一動點，過點P作PD⊥AB，PE⊥AC，垂足分別為D，E,CF為AB邊上的高線．求證：PD+PE=CF.

分析 該例是平面幾何中的一個典型問題，一般采用常規解法，即截長補短法．但是，通過詳細分析發現，題設條件中包含著等腰三角形以及垂線段等特殊條件，因此，我們不禁要問：通過這些條件能否使證法更加簡單呢？

證法1[2](截長法)如圖2所示，過點P作PH⊥FC于點H，易證四邊形DPHF為矩形.因此，PD=FH.

同理，易證Rt△PEC≌Rt△CHP，從而PE=CH，進一步得

PD+PE=FH+CH=CF.

圖2 圖3

證法2[2](截長法)如圖3所示，過點D作DK∥BC交CF于點K，則四邊形DPCK是平行四邊形.由平行四邊形的性質知，PD=CK，DK=PC.因為DK∥BC，所以

∠FDK=∠B=∠PCE.

又因為∠DFK=∠CEP=90°,所以

Rt△DFK≌Rt△CEP,

因此，FK=PE，進一步有

PD+PE=CK+FK=CF.

證法3 (補短法)如圖4所示，過點C作CG⊥DP，交DP的延長線于點G,則四邊形DGCF是矩形，從而FC=DG=PD+PG.進一步有∠PCG=∠B=∠ACP,因此，Rt△PGC≌Rt△PEC,從而PG=PE，于是FC=PD+PE.

圖4 圖5

證法4 (面積割補法)如圖5所示，聯結AP.因為

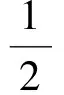
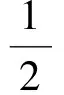
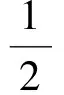
而且S△PAB+S△PAC=S△ABC,所以

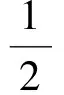
又因為AB=AC，所以PD+PE=CF.

證法5 (三角函數法)如圖1所示，因為△PBD，△PCE和△BCF均為直角三角形，所以

PD=PBsinB，PE=PCsinC，FC=BCsinB.

又因為AB=AC，所以∠B=∠C，sinB=sinC，因此

PD+PE=PBsinB+PCsinC=

(PB+PC)sinB=

BCsinB=FC.

證法6[2](比例化歸法)如圖1所示，容易證明Rt△PBD∽Rt△CBF,從而

(1)

因為AB=AC，所以∠B=∠ACB，從而Rt△PCE≌Rt△CBF,因此

(2)

式(1)+式(2),得

因此

PD+PE=CF.

反思 證法1～3采用的是通法，即求證“一條線段等于另外兩條線段的和”問題，是解決該問題的基本策略[2]；證法4～6則通過挖掘其特殊性，在解題過程中有機滲透數學的轉化思想.例如：由高線想到“面積割補法”(證法4)；由等腰三角形的特殊性質——兩底角相等想到“三角函數法”(證法5)；由3個相似三角形想到比例化歸法(證法6).在方法的變式中，學生的思維得到了發散，在證法的反思中，學生的能力分層得到了體現，教學的效果自然就得到了優化.

2 橫聯縱拓，題目變式

在初三復習教學中，根據問題的特點，設置題目變式，橫向通過類比聯想，縱向通過拓展延伸，“充分挖掘知識之間的聯系，激活學生頭腦中原有的相關知識和經驗”[3]，從而建構起新的知識、方法網絡．

圖6

例2[4]如圖6所示，在△ABC中，分別作它的內角平分線CE和外角平分線CF，求∠ECF的度數.

這是浙教版課標教材七年級下冊第1.2節“三角形的角平分線和中線”第11頁作業題第4題.當學生完成此題的解答后，教師可以通過橫聯縱拓、問題分層，使不同水平的學生在數學學習上得到不同的發展.也可以通過橫向類比聯想，讓學生帶著問題去思考、畫出圖形，并引導學生歸納、總結，最后得到3種不同類型的圖形(如圖7～9)，它們所體現的數學問題分別是[4]：

問題1 三角形不在同一頂點處的內角平分線和外角平分線的夾角問題(如圖7).

問題2 三角形兩條內角平分線的夾角問題(如圖8).

問題3 三角形兩條外角平分線的夾角問題(如圖9).

圖7 圖8 圖9

對于上述3個問題，教師可根據圖形繼續提出問題：“在圖7～9中的∠CPB與∠A之間，分別有著怎樣的關系？”學生的思維再次被激發.

通過對問題1～3的變式訓練，可以有效地培養學生的數學發散思維能力，以及他們的創新意識.如果以上述問題為背景，在原圖形的基礎上對問題結論的規律作進一步的探究(即縱向拓展延伸)，那么學生不僅會一題，而且會一類，從而培養學生知識遷移的能力和應用知識解決問題的能力.

問題4 如圖10，在△ABC中，∠A=α，∠ABC的平分線與∠ACD的平分線交于點A1;∠A1BC的平分線與∠A1CD的平分線交于點A2;…;∠A2 010BC的平分線與∠A2 010CD的平分線交于點A2 011，則∠A2 011為______.

圖10 圖11

問題5 如圖11，在△ABC中，A1B,A1C分別平分∠ABC和∠ACB，A2B,A2C分別平分∠A1BC和∠A1CB,…,A2 011B,A2 011C分別平分∠A2 010BC和∠A2 010CB,則∠A3和∠A有何關系？你能探究出∠A2 011和∠A的關系嗎？繼續下去，若AnB,AnC分別平分∠An-1BC和∠An-1CB，你能用∠A表示出∠An嗎？

圖12

問題6 如圖12，在△ABC中，A1B,A1C分別平分△ABC的外角∠DBC和∠ECB，A2B,A2C分別平分∠A1BC和∠A1CB,…,A2 011B,A2 011C分別平分∠A2 010BC和∠A2 010CB,則∠A3和∠A有何關系？你能探究出∠A2 011和∠A的關系嗎？繼續下去，若AnB,AnC分別平分∠An-1BC和∠An-1CB，你能用∠A表示出∠An嗎？

3 精講精練，過程變式

過程性變式是指在數學活動過程中，通過有層次的推進，使學生在分步解決問題中，積累多種活動經驗、發展學生智力、提高運用知識能力的教學活動.復習課要做到精講精練是不容易的,“精講”不能理解為“少講”，而是該講的重點、難點,關鍵點要講深、講透；“精練”也不等于“少練”，而是該練的精編或精選題要練足、練全．

1)求點A,B,C的坐標；

2)求證：△ABC是直角三角形；

3)若坐標平面內的點M，使得以點M和點A,B,C為頂點的四邊形是平行四邊形，求點M的坐標(直接寫出點的坐標，不必寫求解過程)．

這是一道集代數(二次函數、二次方程)、幾何(直角三角形、平行四邊形)等重點知識于一體的中考試題.如何在講授完該題之后，進一步拉長“知識鏈”，提出適合于不同層次學生需求的問題，讓他們在解決問題的過程中積累解題經驗，這需要教師課前進行精心預設．

通過變式1可以清楚地認識到：有些圖形的對稱性問題不一定需要通過圖形去求解，而是可以通過挖掘出題目中隱含的規律，運用新的解題方法來解決．線由點組成，線的對稱可以轉化為點的對稱，因此，關于x軸對稱，即將y用-y替換，x不變；關于y軸對稱，即將x用-x替換，y不變；關于原點對稱，即將x用-x替換，將y用-y替換即可[5].

變式2 求△ABC的外接圓半徑和內切圓半徑．

變式3 點G為直角坐標平面內的一點，若以點A,B,C,G為頂點的四邊形是矩形，求點G的坐標．

變式2和變式3是基礎題，初三課堂教學要有一種保底意識，通過問題的分層，使一些暫時基礎較差的學生也學有所獲，而對基礎較好的學生來說也能進一步打好知識基礎.

變式4 在△ABC內部能否截出面積最大的矩形DEFG(頂點D,E,F,G在△ABC各邊上)？若能，求出在邊AB上的矩形頂點的坐標；若不能，請說明理由．

變式5 將△AOC沿y軸對折后，再繞點C按逆時針方向旋轉90°得到△CFE(點A與點E對應)，判斷點E是否在拋物線上，并說明理由．

變式6 設過點E的直線交邊AB于點P，交邊BC于點Q，使直線PQ分△ABC的面積為1∶3兩部分？若存在，求出點P的坐標；若不存在，請說明理由．

變式7 在已知拋物線的對稱軸上找一點P，使得△APC的周長最小，求點P的坐標及△APC的最小周長．

評注 課堂教學要抓中間促兩頭，變式4～7為中檔題，這是復習教學中要下力氣重點抓好的一檔題，使一些暫時基礎較差的學生“跳一跳也能摘得到”，而對基礎較好的學生來說，這也是需要認真去做的問題.

變式8 若一個動點M自點P(0，1)出發，先到達對稱軸上某點(設為點F),最后運動到點C.試確定使點M運動的總路徑最短的點E和點F的位置，并求出這個最短路程的長[6]．

變式9 若一個動點M自點P(0，1)出發，先到達x軸上的某點(設為點E)，再到達拋物線的對稱軸上某點(設為點F),最后運動到點C.試確定使點M運動的總路徑最短的點E和點F的位置，并求出這個最短路程的長[6]．

變式10 若點Q是拋物線對稱軸上的一個動點，點R是拋物線上的一個動點，使得以A,B,Q,R為頂點的四邊形為平行四邊形，求點R的坐標．

變式11 聯結BC，點D是直線BC上方的拋物線上的一個動點，問：當點D運動到什么位置時，△BCD的面積最大？求此時點D的坐標和△BCD的最大面積．變式12 若平行于x軸的直線與該拋物線交于點H，K，且以HK為直徑的圓與x軸相切，求此時圓的半徑．

評注 變式8～12為稍難題，涉及最值問題、動點問題、分類討論問題、轉化思想、方程思想等，都是初中數學中最為重要的數學問題、數學思想.課堂要有靈動，需要對各層次學生的尊重，教學中既要有“保底”意識，也要有“探究”的勇氣.教師要善于對已有的問題進行加工、變式、改造、整合，不斷利用已有經驗對問題進行變通推廣、探索引申、提煉升華，以激發學生學習數學的興趣，提升學生的創新思維能力.

總之，“數學復習課教學的優化”是一個永恒的話題，課堂的有效、高效是我們堅持不懈的追求.在復習課教學中，教師要以教材中的經典問題、生活中的數學問題、新穎別致的中考試題為切入點，充分挖掘典型問題的教學價值，通過變式教學、分層教學，使不同層次的學生在原有基礎上都有所提高，使“不同的人在數學上得到不同的發展”的理念得到體現.雖然在目前班級授課制下，要真正做到教學面向全體學生實施分層教學、合理有效地進行變式教學難度較大，但仍值得我們繼續去研究和探索．

[1] 林丹群,莊靜云,陳清華.2011年“華約”自主招生筆試試卷評析暨2012年備考建議[J].福建中學數學,2011(11):6-11.

[2] 董玉峰.深化教學改革,構建高效課堂[ED/OL].https://wenku.baidu.com/view/562bd566caaedd3383c4d3b7.html,2012-11-27.

[3] 張國富.精制精導,點燃學生心智——淺談一道源于課本的考題及其變式[J].青少年日記:教育教學研究,2013(7):40.

[4] 龍普云.從幾道中考題說開[ED/OL].http://www.docin.com,2012-11-13.

[5] 邢成云.題組引領 梯度推進——例談題組梯度復習法[J].中國數學教育,2010(Z2):34-37.

[6] 黃小芹.“線段之和最短問題”初探[J].中學數學,2012(8):66-67.

1 直覺性思維——反思的萌芽

圖1

一般利用重心在向量中的表示形式來解決.

S△AOE=S△AOD=S△DOE.

易知S△AOD=2S△AOB,S△AOE=3S△AOC,S△DOE=6S△BOC,于是

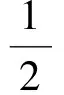
就題目而言，我們已經解決，但如果能再仔細觀察一下，發現答案3∶2∶1和題干中3個向量的系數比是一樣的，這是巧合還是一般性結論，直覺告訴我們不能僅僅滿足于答案，而應對此作進一步的反思和研究.

2 直覺到一般——反思的產生

通過直覺，筆者猜想如下的定理：

圖2

證明 延長AO交BC邊于點D.因為

所以

于是

上面證明了點O在△ABC內的情況，進一步反思：如果點O在△ABC外，是否還有同樣的結論呢？仿照上面的推理過程，不難得到如下結論：

定理2 設O是△ABC外任意一點，△OBC,△OAC,△OAB的面積分別為S1,S2,S3.

1)當點O與點A在BC的異側時，若S△OBC∶S△OAC∶S△OAB=λ∶u∶v,則

2)當點O與點B在AC的異側時，若S△OBC∶S△OAC∶S△OAB=λ∶u∶v,則

3)當點O與點C在AB的異側時，若S△OBC∶S△OAC∶S△OAB=λ∶u∶v,則

筆者從一個基本題目出發，通過反思發現了一般性的結論，在教學中反思能更有效地鞏固基礎，提高知識和方法的認識水平，通過有意識地反思，明確題目所覆蓋的知識點，思考解決這類問題的一般方法.

3 一般性的延伸——反思的深化

此時，似乎已經完美地尋求到了問題的解決方案，愛思考的學生往往會對問題作進一步的反思.很多涉及到三角形的四心(重心、內心、外心、垂心)和向量結合的問題，能否利用上面的結論來建立一個統一形式？沿著這個思路繼續思考問題，得到如下的定理：

1)若點O為△ABC的重心，則

λ1∶λ2∶λ3=1∶1∶1；

2)若點O為△ABC的外心，則

λ1∶λ2∶λ3=sin 2A∶sin 2B∶sin 2C；

3)若點O為△ABC的內心，則

λ1∶λ2∶λ3=a∶b∶c；

4)若點O為△ABC的垂心，則

λ1∶λ2∶λ3=tanA∶tanB∶tanC.

前面3個結論比較容易得到，下面對第4)個結論進行證明.

證明 如圖3，因為H是△ABC的垂心，所以

圖3

又因為四邊形AEHF的頂點A,E,H,F共圓，所以

∠A+∠BHC=π，

同理可得 ∠B+∠AHC=π，

故S△BHC∶S△CHA∶S△AHB=tanA∶tanB∶tanC.

利用化歸的思想，通過一步一步反思，把這些看起來互不相關的問題都統一到一個形式上.羅增儒老師把解題后缺乏反思的現象比喻為“進寶山而空手返”.通過對已完成的思維過程進行周密且具有批判性地思考，進一步來探討知識的內涵和外延，從中領悟數學思想方法，形成良好的認知結構，從而提高學生的元認知水平，完善知識體系.

4 成果應用——反思的再認識

通過以上的反思，學生的思維能力得到了提升，對問題的理解能力也更加深刻，下面我們把這些反思的成果應用到日常的解題中.

解 根據定理3，因為G為△ABC的重心，所以

56a=40b=35c，

即

代入余弦定理，得

故

整理得

則

m∶n∶(1-m-n)=5∶5∶6,

解得

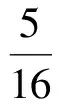
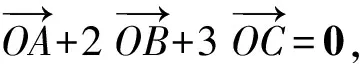
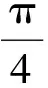
(2016年山東省高中數學聯考試題第5題)

解 因為P為△ABC的外心,所以

根據已知條件，得

sin 2A=sin 2B，

又∠C=120°，從而

于是

故λ=-1.

筆者以一道常見數學題目為例，闡述了在數學教學過程中不斷思考、不斷反思問題以達到不斷優化的目的.數學教學離不開解題教學，解題教學是數學教學的一個重要組成部分，在解題教學過程“如何引導學生思考、如何反思”是教師的一項重要工作.若平時在教學過程中能經常滲透這種意識，則學生會不斷地實踐并學會數學地思考問題，數學素養和數學品質也定能得到相應提升.

2017-06-30

童桂恒(1963-)，男，浙江開化人，浙江省特級教師.研究方向：數學教育.

O123.1

A

1003-6407(2017)09-01-04