對初中數(shù)學應用題教學的一點思考

繆輝平

【摘要】在實際生活中，方案設(shè)計問題也是多種多樣，如裁料方案、測高方案、調(diào)運方案.有的方案設(shè)計要涉及可行性的討論和最佳性的選擇，日新月異的社會變化、豐富多彩的實際生活，要求應用題設(shè)計要與時俱進，只要我們了解了這個新的趨勢，在數(shù)學教學中適當加強訓練，就可以以不變應萬變，把握好成功的機會.

【關(guān)鍵詞】初中數(shù)學；應用題；教學思考

科學地認識事物就要抓住事物的本質(zhì)，那么列方程解應用題的本質(zhì)是什么呢？很顯然，列方程（組）是關(guān)鍵.所謂列方程（組）解應用題是一個“實際”問題，以文字表達形式出現(xiàn)，然后，運用數(shù)學方法將應用題的內(nèi)涵符號化成為一個方程（組），再解所列方程（組）從而應用題得解，因此，在應用題的教學時，應把難點放到分析題意列出方程（組），并讓學生熟練掌握應用題符號化這一步驟，這樣方程（組）就列出了，當然學生剛剛接觸應用題時可能有些難度，但按照教材的編排，在學習列方程（組）解應用題之前就學習了用代數(shù)式表示各種各樣背景下的實際問題，也學習了解方程和解方程組，學習了行程、速度、時間之間的關(guān)系，學習了工作總量、工作效率、工作時間之間的關(guān)系，學習了銷售中的本金、利潤、利率之間的關(guān)系，等等.

初中數(shù)學中的應用題是建立在小學的基礎(chǔ)上的，而且是從“行程問題”入手，因此，在一開始進行“行程問題”的教學時就必須強調(diào)要求畫“s，v，t”表格：

來幫助分析，且要掌握好公式：路程（s）=速度（v）×時間（t），而且初中階段的大多數(shù)應用題都可以借助“s，v，t”表格來幫助分析，如“工程問題”.

例1A，B兩地相距360 km，甲、乙兩輛車分別從A，B兩地同時出發(fā)相向而行，甲車的速度是70 km/h，乙車的速度是50 km/h，求甲、乙兩車出發(fā)后經(jīng)過幾小時相遇？

解設(shè)甲、乙兩車出發(fā)后經(jīng)過x小時相遇.

分析：（一）找等量關(guān)系：① 甲車的行駛時間（t甲）=乙車的行駛時間（t乙）；

② 甲車的行駛路程（s甲）+乙車的行駛路程（s甲）=360.

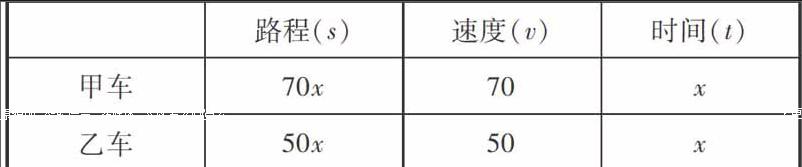
（二）畫“s，v，t”表格：

（三）列方程：

因為等量關(guān)系① 甲車的行駛時間（t甲）=乙車的行駛時間（t乙）在畫“s，v，t”表格時已經(jīng)用過.因此，只能根據(jù)等量關(guān)系②甲車的行駛路程（s甲）+乙車的行駛路程（s乙）=360.列方程得

70x+50x=360.

解這個方程得x=3.

答：甲、乙兩車出發(fā)后經(jīng)過3小時相遇.

強調(diào)：① 認真理解題意，弄清題目中事件發(fā)生過程及其各個量之間內(nèi)在的等量關(guān)系，每個等量關(guān)系只允許用一次；

② 畫“s，v，t”表格，并填寫“s，v，t”表格，這樣可大大地減少犯低級錯誤；

③ 根據(jù)未用過的等量關(guān)系來列方程.

并且在以后所有應用題教學引導中都要這樣“強調(diào)”，讓學生形成思維習慣.

例2A，B兩地相距35 km，甲從A地向B地出發(fā)5 km，乙在A地發(fā)現(xiàn)甲忘記帶某文件立即追送，交給甲后立即返回A地，當乙返回A地時，甲恰好到達B地，乙每小時比甲多行5 km，求兩人的速度.

解設(shè)甲的速度是x km/h.

分析：（一）畫行程圖，找出等量關(guān)系.在這必須認真理解題意，弄清楚整個事件發(fā)生過程，才能畫出行程圖.

從行程圖中看到：甲從C點到D追及點的時間（t甲CD）與乙從A點到D追及點的時間（t乙AD）是相等的，乙從D追及點返回A點的時間（t乙DA）與甲從D追及點到B點的時間（t甲DB）也是相等的.即t乙AD=t乙DA=t甲CD=t甲DB.

因此，CD=DB=15，AD=AC+CD=20.

找到等量關(guān)系：① 乙的速度（v乙）=甲的速度（v甲）+5；

② 甲行進15 km的時間（t甲15）=乙行進20 km的時間（t乙20）.

（二）畫“s，v，t”表格：

解這個方程得x=15.

經(jīng)檢驗得x=15是所列方程的解.因此，x+5=20.

答：甲的速度是15 km/h，乙的速度是20 km/h.

此題中列方程要用到的等量關(guān)系②甲行進15 km的時間（t甲15）=乙行進20 km的時間（t乙20）沒有明確表示出來，是隱藏于題目內(nèi)的，需要認真地理解題意，并要借助行程圖才好找.

列方程解應用題的一般基本步驟為：

（一）審題（主要完成如下三方面的工作）：

1.分析條件（對條件要進行歸納分類），認真理解題意，弄清題目中事件發(fā)生過程及各個量之間內(nèi)在聯(lián)系，可借畫“s、v、t”表格幫助理解.

2.明確已知量和未知量.

3.找出等量關(guān)系，每個等量關(guān)系只允許用一次.

（二）解題的實施：

1.設(shè)未知數(shù)（或稱設(shè)元）.

2.根據(jù)等量關(guān)系列出方程（組）.

3.解方程（組），并檢驗.

4.答.

學生列方程（組）解應用題的困難主要來自如下三方面：

第一，審題沒有養(yǎng)成習慣，對文字圖形理解能力低下，缺乏生活實踐知識，根本弄不清題意，有的雖然審題，但審題缺乏邏輯性和系統(tǒng)性.其突出表現(xiàn)在于對審題的基本要求是什么不明確，對題目中的條件不習慣于歸納分類.因而，造成考慮問題不是全局化、透徹化，而是孤立的、表面地理解條件，甚至遺漏條件.

第二，用代數(shù)式表示各種實際問題中的量、解方程（組）等與基礎(chǔ)知識脫節(jié)，比如，弄不清楚銷售中的銷售額、標價、售價、本金、利潤、利率之間的關(guān)系.

第三，不明確（或沒注意）列方程的基本標準，列出與實際意義不相符（錯誤）的方程.我們常常發(fā)現(xiàn)學生列出來的方程兩邊的意義不同，也發(fā)現(xiàn)一個代數(shù)式所表示的意義混亂，如，把速度與時間相加（或相除）的代數(shù)式.

鑒于上述三點，在教學上應采取什么措施以便降低錯誤率呢？我認為，應注重如下幾方面.

1.應堅持系統(tǒng)性原則，可以這么認為，列代數(shù)式的訓練是列方程解應用題的前奏，故應該全力爭取使學生在列代數(shù)式階段能具備較完善的由語言信息轉(zhuǎn)化到數(shù)學式子（代數(shù)式）的能力，事實上，現(xiàn)行教材已經(jīng)有足夠的內(nèi)容使之達到這個要求的.就是列方程解應用題本身看，也是分階段的（如，一元一次方程，二元一次方程，一元二次方程，二元二次方程等）.在諸多階段中，應該算一元一次方程的應用題最為關(guān)鍵，若這一關(guān)過不好，很難保證今后學習會順利.因此，教師在整個初中數(shù)學教學上應全面考量.

2.要嚴格審題程序，弄清題目中事件發(fā)生過程及其各個量之間內(nèi)在的聯(lián)系，這方面教師在平時教學中應落實提高學生的文字理解能力，準確地將文字語言轉(zhuǎn)化成數(shù)學語言.

3.明確列方程解應用題的基本要求.主要明確三點：（1）在同一方程里，兩邊的意義要相同，如不要一邊是距離，另一邊又是時間；（2）同一方程里的各項的單位要統(tǒng)一，如不要一些是小時，一些又是分鐘；（3）方程兩邊的數(shù)量要相等，符合實際意義等.

4.注意總結(jié)方程應用題的類型的基本關(guān)系式.如，路程=速度×時間；工作量=效率×時間；工作總量=各部分工作量之和等；利潤=本金×利率=營業(yè)額-本金.

通過數(shù)學建模，既考查從數(shù)學的角度觀察、思考和分析實際問題的能力，又考查對相關(guān)知識（包括數(shù)學的、生活的、社會的、自然的，乃至文化的多方面的知識）和技能的理解和掌握程度.從而能比較好地反映學生對信息的接收、加工和輸出能力，達到有效考查綜合素質(zhì)的目的.所以，平時要加強運用數(shù)學意識的培養(yǎng)，學會數(shù)學地思維.