以豐富實例為背景學習數學

朱燦

【摘要】“一次函數”是在認識了函數、函數的圖像和正比例函數的基礎上進行的，一次函數是最基本、最簡單的函數，本節課主要學習一次函數的概念.本節內容既是前面知識的深化和應用，又為今后學習反比例函數、二次函數的概念，提供了一般思路和方法.因此，本節課具有承上啟下的重要作用，在函數的學習中起到非常重要的作用.

【關鍵詞】數學教學；一次函數；教學設計

一、“一次函數”的學習目標

《數學課程標準（2013年版）》中關于“一次函數”的學習，具體目標是：

1.結合具體情境體會一次函數的意義，根據已知條件確定一次函數表達式.

2.會畫一次函數的圖像，根據一次函數的圖像和解析式y=kx+b（k≠0）探索并理解其性質（k>0或k<0時，圖像的變化情況等）.

3.理解正比例函數.

4.能根據一次函數的圖像求二元一次方程組的近似解.

5.能用一次函數解決實際問題.

6.培養學生積極探索的精神以及觀察、分析、總結的良好學習習慣.

本節課要求學生能借助教科書中的問題和大量的實例的研究，提煉出一次函數的概念，并能通過對比，發現正比例函數解析式和一次函數解析式之間的關系，體會解決問題過程當中合作交流的重要作用.通過探究歸納一次函數的概念，體驗研究函數概念的一般思路與方法.

二、“一次函數”的教學設計

由常量數學到變量數學，是在數學思維上的一次飛躍.新版數學教材更是注重了函數思想的滲透.通過對課程標準的學習可以發現：《標準》強調豐富實例為背景，在應用方面提出了更高的要求，對函數模型認識要求也有所提高.本文結合教材和“一次函數”的教學實際，略談一二.

例如，為支持四川抗震救災，重慶市A、B、C三地現在分別有賑災物資100噸、100噸、80噸，需要全部運往四川重災地區的D、E兩縣.根據災區的情況，這批賑災物資運往D縣的數量比運往E縣的數量的2倍少20噸.

（1）求這批賑災物資運往D、E兩縣的數量各是多少？

（2）若要求C地運往D縣的賑災物資為60噸，A地運往D縣的賑災物資為x噸（x為整數），B地運往D縣的賑災物資數量小于A地運往D縣的賑災物資數量的2倍.其余的賑災物資全部運往E縣，且B地運往E縣的賑災物資數量不超過25噸.則A、B兩地的賑災物資運往D、E兩縣的方案有幾種？請你寫出具體的運送方案.

（3）已知A、B、C三地的賑災物資運往D、E兩縣的費用如下表所示.

1A地1B地1C地運往D縣的費用（元/噸）122012001200運往E縣的費用（元/噸）125012201210為及時將這批賑災物資運往D、E兩縣，某公司主動承擔運送這批賑災物資的總費用，在（2）問的要求下，該公司承擔運送這批賑災物資的總費用最多是多少？

解析本題題干文字長，數量關系復雜，但只要弄懂了題意，并結合表格將數量關系進行整理，解決起來并不難.

（1）直接用一元一次方程求解.運往D縣的數量比運往E縣的數量的2倍少20噸，設運往E縣m噸，則運往D縣（2m-20）噸，則m+（2m-20）=280，m=100，2m-20=180.（亦可用二元一次方程組求解）

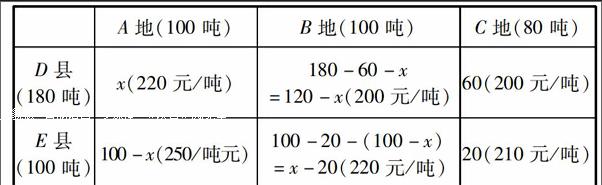
（2）由（1）中結論，并結合題設條件，設由A地運往D縣的賑災物資為x噸，相應數量關系如下表所示.

1A地（100噸）1B地（100噸）1C地（80噸）D縣

（180噸）1x（220元/噸）1180-60-x

=120-x（200元/噸）160（200元/噸）E縣

（100噸）1100-x（250/噸元）1100-20-（100-x）

=x-20（220元/噸）120（210元/噸）表格說明：① A、B、C、D、E各地后括號中的數字為調運量或需求量；② 表格中含x的式子或數字，表示對應地點調運數量；③ 表格中其他括號中的數字，表示對應的調運費用.

確定調運方案，需看問題中的限制條件：① B地運往D縣的賑災物資數量小于A地運往D縣的賑災物資數量的2倍.② B地運往E縣的賑災物資數量不超過25噸.故：

120x-x<2x，

x-20≤25， 解得x>40，

x≤45， ∴40

∵x為整數，

∴x的取值為41，42，43，44，45，則這批救災物資的運送方案有五種.

方案一：A縣救災物資運往D縣41噸，運往E縣59噸；

B縣救災物資運往D縣79噸，運往E縣21噸.

（其余方案略）

（3）設運送這批賑災物資的總費用為y元，由（2）中表格可知：

y=220x+250（100-x）+200（120-x）+220（x-20）+200×60+210×20=-10x+60800.

∵y隨x增大而減小，且40

∴當x=41時，y有最大值.

該公司承擔運送這批賑災物資的總費用最多是

y=-10×41+60800=60390（元）.

三、教學反思

“函數及其圖像”這一章的重點是一次函數的概念、圖像和性質，一方面，在學生初次接觸函數的有關內容時，一定要結合具體函數進行學習，因此，全章的主要內容是側重在具體函數的講述上的.另一方面，在《數學課程標準》規定的幾種具體函數中，一次函數是最基本的，教科書對一次函數的討論也比較全面.通過一次函數的學習，學生可以對函數的研究方法有一個初步的認識與了解，從而能更好地把握學習二次函數、反比例函數的學習方法.