n階行列式第一課的教學(xué)探討

文/毛元福 孫小迎

n階行列式第一課的教學(xué)探討

文/毛元福 孫小迎

《線性代數(shù)》是理工科大學(xué)學(xué)生的一門必修基礎(chǔ)數(shù)學(xué)課程，生產(chǎn)實(shí)際和科學(xué)研究中有許多問題可以歸結(jié)為線性方程組，行列式正是對線性方程組的研究中建立起來的。行列式的計(jì)算是線性代數(shù)中的重點(diǎn)難點(diǎn)，特別是n階行列式的計(jì)算，學(xué)生在學(xué)習(xí)過程中，普遍存在很多困難，難于掌握。因而對于初學(xué)線性代數(shù)的同學(xué)來說，行列式的第一課尤為重要，既要讓學(xué)生較容易的掌握行列式的基本概念，還要激發(fā)學(xué)生進(jìn)一步學(xué)習(xí)行列式強(qiáng)烈愿望。本文就行列式的第一課做了一些結(jié)構(gòu)性的教學(xué)探索。

n階行列式的計(jì)算是線性代數(shù)中的一個(gè)重要問題，也是一個(gè)很復(fù)雜的問題，其技巧性很強(qiáng).理論上任何一個(gè)n階行列式都可以按定義計(jì)算，但是當(dāng)n較大時(shí)，直接按定義計(jì)算而不借助于計(jì)算機(jī)幾乎是不可能的.因此，探尋n階行列式的計(jì)算方法是十分必要的.

《線性代數(shù)》第一課一般安排的教學(xué)任務(wù)是一些基本的概念，比如排列，標(biāo)準(zhǔn)排列，逆序數(shù)，排列的奇偶性，對換，在此基礎(chǔ)上引入二、三階行列式的概念及其計(jì)算方法，這些概念學(xué)生也容易理解，但是由于學(xué)生還不了解二、三階行列式的運(yùn)用領(lǐng)域，這個(gè)時(shí)候?qū)W生只是被動接受二、三階行列式的計(jì)算方法，也不能調(diào)動學(xué)生學(xué)習(xí)《線性代數(shù)》新知識的積極性和興趣。

為引起學(xué)生的注意力和探索新知識的積極性，《線性代數(shù)》第一課可以做一些結(jié)構(gòu)性的調(diào)整。首先導(dǎo)入一個(gè)沒有難度系數(shù)的二元一次方程組，和學(xué)生們一起運(yùn)用熟知的加減消元法很快地求得方程組的解為，再引出二元一次方程組的一般形式，這里的x1，x2是未知數(shù)，a11，a12，a21，a22，b1，b2，均為常數(shù)，當(dāng)a11a22-a12a21≠0時(shí)，同樣運(yùn)用加減消元法容易得到方程組的解為，很顯然這可以作為二元一次方程組的一般形式在a11a22-a12a21≠0時(shí)的求解公式，其形式復(fù)雜，難于識記。

這時(shí)我們把二元一次方程組一般形式的未知數(shù)的系數(shù)a11，a12，a21，a22，按規(guī)律寫成數(shù)表，并記D==a11a22-a12a21≠0，也就是引入一種新的運(yùn)算法則（這個(gè)法則有些學(xué)生在初中見過），數(shù)表中的4個(gè)元素是有二元一次方程組的一般形式未知數(shù)的系數(shù)構(gòu)成的二行二列矩形數(shù)表，把這個(gè)二行二列矩形數(shù)表就定義為二階行列式，它的值就按D==a11a22-a12a21計(jì)算，即把左上角到右下角稱為主對角線，把右上角到左下角稱為副對角線，二階行列式的值就等于主對角線兩個(gè)元素的積減去副對角線兩個(gè)元素的積，這就是二階行列式運(yùn)算的對角線法則。

如果把b1，b2同樣看做一列去替換D=中的第一列可得D1==b1a22-a12b2，把b1，b2同樣看做一列去替換D=中的第二列可得D2==a11b2-b1a21，因而二元一次方程組的一般形式的解就可以簡單地表示為x1=， x2=，容易識記，但運(yùn)算量并未減少，體現(xiàn)不出這個(gè)公式的優(yōu)勢。這時(shí)提出解三元一次方程組能否運(yùn)用這種思想方法呢？啟發(fā)學(xué)生思考。

其中主對角線上3個(gè)元素的積取正號，副對角線上3個(gè)元素的積取負(fù)號（提示學(xué)生符號還有其它方法來確定，為后面講述逆序數(shù)等概念做鋪墊），且3個(gè)元素都取自不同行不同列，再將b1，b2，b3作為一列替換D中第一列得到D1=，替換D中第二列得D2=，替換D中第三列得D3=，當(dāng)D≠0時(shí)，可得這個(gè)三元一次方程組的解：x1=，x2=，x3=，其正確性可由來驗(yàn)證，運(yùn)算量顯然增加了，尤其是對角線法則不能適用16個(gè)元素排成的四行四列的四階行列式D=及n2個(gè)元素排成的n行n列的n階行列D=式的計(jì)算，而前面推導(dǎo)二元線性方程組、三元線性方程組解的公式形式卻可以類比運(yùn)用到四元線性方程組及n元線性方程組。

此時(shí)直接引出定理Cramer法則：設(shè)有線性方程組

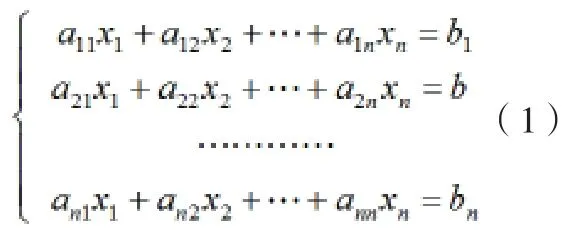
由定理Cramer法則讓學(xué)生們確信運(yùn)用行列式解n元線性方程組是一個(gè)行之有效的法則，到這里學(xué)生們明白了學(xué)習(xí)行列式的意義，因?yàn)橹灰苡?jì)算n階行列式D的值，就可以求解n元線性方程組，從而能激發(fā)學(xué)生們學(xué)習(xí)n階行列式D計(jì)算的濃厚興趣。這個(gè)時(shí)候回過來講解諸如排列，標(biāo)準(zhǔn)排列，逆序數(shù)，排列的奇偶性，對換等一系列基本概念，學(xué)生們表現(xiàn)更期盼學(xué)習(xí)下一節(jié)行列式的性質(zhì)與計(jì)算，變被動學(xué)習(xí)為主動學(xué)習(xí)。

（作者單位：南昌工學(xué)院 民族教育學(xué)院）