思維的增量在哪里
———以《20以內退位減法》復習課為例

孫其英

小學生學習數學的過程是一個不斷再創造，形成新的知識結構，并促進思維能力螺旋上升的過程。在這個過程中，每一節數學課的思維增量，支撐著學生思維能力的提高。

一、在學生想不到的地方設計問題，鍛煉思維的全面性

課堂片斷一：課始，出示（）－7=比6大，填填看，你是怎么想的？

學生紛紛進行填寫，反饋有兩種想法：

生1：填一個數字，算一算，看差是不是比6大，所以，填寫了 17、14、16 等。

生2：我也是，一開始試了10、13，發現差沒有比6大，后面試的都可以。

學生想不到的地方：一年級的學生思維還處于感性思維占主體階段，嘗試法是他們學習數學常用的方法，在這個練習中，學生利用嘗試法進行計算，得出結果。可以從幾開始想，答案有幾個，要注意什么，這些都是學生想不到的地方。

教學策略：針對學生的思維特點，設計問題：從幾開始寫？要注意什么？

課堂再現：

問題1：從幾開始寫？

師：剛才報了好多答案，那么，從幾開始寫呢？

生1：從14開始寫。我是從差開始想的，因為差要比6大，可以是7、8、9……，（ ）-7=7、（ ）-7=8、（ ）-7=9……所以，被減數就是 14、15、16……

生2：先寫13，我是與13-7=6進行對比，因為差要比6大，所以，被減數13是不夠的，那可以是 14、15、16……，所以，從 14 開始寫。

問題2：要注意什么？

將（ ）-7=比6大過渡到（ ）-7＞6，并出示13-（）＞6，填填看，從幾開始填？

生1：從6開始填。我想答案要大于6，可以是 7、8、9 等，13-（）=7,13-（）=8,13-（）=9，就可以得出（）從6開始填。

生2：從6開始填。我是與13-7=6進行比較，答案比6大，也就是減去的數要比7小，可以從6開始填寫。

師：要注意什么？

生3：要注意不要漏掉0，應該是6～0。

生4：是的，我剛才就是6～1。

【教學思考：問題“從幾開始寫”，讓學生的思維趨于有序，一開始的嘗試填寫，從無序填寫，到有序思考，是思維上的一個跨越。通過問題“要注意什么”，提醒學生要注意容易漏掉的“0”，使思維更趨于完整、全面。通過看似平常的兩個問題，在學生想不到的地方，關注了思維的有序性，關注了“0”這個易漏點，讓學生的思維經歷從一開始的無序到有序，從隨意到嚴謹，做到不重復、不遺漏。】

二、在學生想不深的地方資源鏈接，培養思維的深刻性

課堂片斷二：出示（）-（）=6，你有什么發現？

生1：7-1=6開始填寫，一直到20-14=6。

生 2：20-14=6，一直到 7-1=6。

生3：還有6-0=6，不能漏掉。

師：你有什么發現嗎？

生4：被減數有規律，減數有規律。

教學策略：學生對單列數據已經感悟到填寫規律，但不能深入思考算式整體之間的關系。這時，我采用資源鏈接法，用數形結合和生活中的年齡問題來幫助學生深入思考。

課堂再現：

師：這類問題比較抽象，讓圖形來幫助我們吧。

鏈接1：數形結合。

圖1　

圖2　

圖3　

圖4　

圖5　

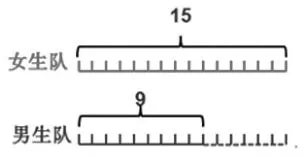
圖6　

從圖1到圖2，用長方形表示，兩個隊始終相差6，我們可以繼續表示一直到20-14=6；從圖2到圖3，把長方形豎起來，兩個隊還是相差6；從圖3到圖4，把長方形壓扁，變成小正方形，仍舊表示兩個隊相差6；從圖4到圖5，繼續壓扁，變成兩根線段，還是表示兩個隊相差6；從圖5到圖6，將相差部分從左邊移到右邊，也是表示相差6。

鏈接2：年齡問題。

師：（ ）-（ ）=6，還可以怎樣想呢？讓生活經驗來幫我們理解吧！

出示一組班級中小朋友的姐弟照片，出示他們的年齡：

師：他們都可以用（ ）-（ ）=6來表示，這就是生活中的數學問題。那么，小明10歲時，姐姐幾歲呢？姐姐20歲時，小明幾歲呢？

生：小明10歲時，姐姐16歲，因為（16）-（10）=6；姐姐20歲時，小明14歲，因為（20）-（14）=6。

【教學思考：從長方形到壓扁的小正方形，再到線段，是一個漸進的過程，也是從平面圖形到線段的抽象過程，為今后的線段圖學習奠定基礎。數學源于生活，生活中處處有數學。年齡是學生的生活經驗，遷移生活經驗來理解抽象的（）-（）=6，讓學生感受到數學不再是抽象的。在學生想不深的地方，運用資源鏈接，數形結合，遷移生活經驗，鍛煉思維的深刻性，思維就有了增量。】

三、在學生想不透的地方滲透代數結構，促進思維的靈活性

課堂片斷三：出示13-7=（ ）-6，你是怎么想的？

生 1：因為 7-1=8-2=9-3=……=6，所以，括號里填12。

生2：因為左邊等于6，右邊也要等于6，所以，括號里填12。

師：對了，這樣的題目我們以前叫它“火車車廂”算式（即將算式看成是一節“車廂”，每節車廂得數相等，類似天平原理），那你能填寫下面這題嗎？

出示：（ ）-7=（ ）-6，你有什么發現？

生3：根據“火車車廂”原理填的，兩邊都等于6，所以，填 13 和 12。

師：還有其他的嗎？

（學生進入思考，一時沒人舉手）

教學策略：像這一類比較抽象的等式問題，我采用滲透代數結構的方法，促進學生思維的靈活性。

課堂再現：

師：除了兩邊都等于6，還可以等于其他數嗎？

生1：可以等于5，那就填12、11，也可以等于其他數。

師：還可以怎么想？

生2：還可以這樣想，減數7到6減少了1，那被減數也減少1就好了，所以，只要是第一個被減數比第二個被減數大1的，都可以。

師：說得真好！要解決（ ）-7=（）-6，不僅可以考慮等號兩邊的關系，還可以考慮減數之間的規律導致被減數之間的規律，因為減數少1，要使差相等，被減數也要少1。這種從算式的結構角度去思考，叫代數結構思維，是系統解決問題的好辦法。

【教學思考：要解決（ ）-7=（ ）-6，不僅是一種逆向思維，要考慮等號兩邊的關系，還要考慮減數之間的規律導致被減數之間的規律，才能靈活地進行解決，這正是學生想不透的地方。從考慮數的規律到考慮算式整體的規律，學生的思維有了一定的增量，那么學生的思維就靈活了。】