開冪分的概念

合肥工業大學食品科學與技術學院生物工程16-1班 李澤宇

開冪分的概念

合肥工業大學食品科學與技術學院生物工程16-1班 李澤宇

在高中時期，我便第一次接觸了微積分，并學會了一些相關的知識，到了大學，我學的微積分又更上一個臺階，其中有泰勒中值定理，常微分方程，還有我印象最深的牛頓-萊布尼茨公式。牛頓-萊布尼茨公式巧妙地將一個看似無窮的連續函數值的和變成另一個函數的兩個值的差，這讓我領會到數學的奇妙。同時我也在想，牛頓—萊布尼茨公式實質上是一種求和轉換，那么有沒有一個公式是求積轉換呢？思考了很久，我終于找到了，其實只要把微積分里的加減換成乘除，把乘除換成次方和開方，那么就很容易地得到了一個新的數學概念，我把它叫作開冪分，也叫開分和冪分。那么首先像微積分里的微分一樣，我要先介紹一下開分的概念：

一、開分的定義

由開分的定義，我們可以輕易地得到下面的這個性質：

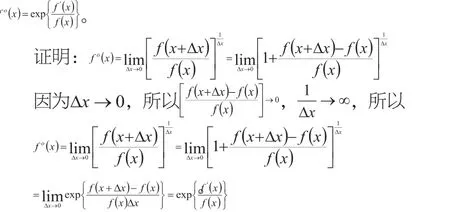
即證。

由這個性質，我們可以得知，如果一個函數可導，那么它一定可以開分。所以函數可以開分的充分條件就是函數可導。

二、基本初等函數的開分

三、開分的運算法則

因為有萬能的這個性質：所以我們可以根據求導的運算性質來做。下面給出一些：

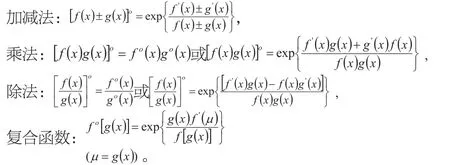
四、冪分的定義

介紹完開分，那么冪分就很好理解了，因為就像微分和積分一樣，冪分就是開分的逆運算，下面給出冪分公式的定義：

將區間[a，b]分成n-1個小區間，記：

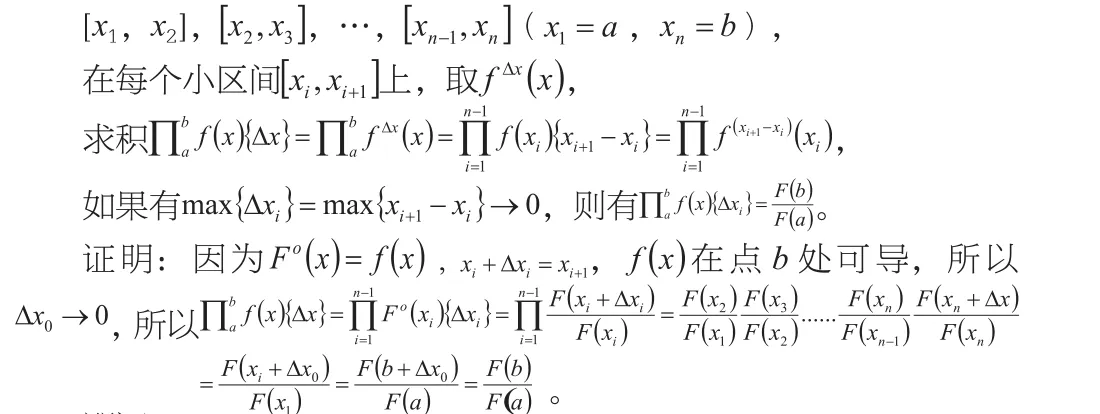
即證。

對于這個公式，在我看來，好像現實中沒有一個實例與它對應，可能是因為我的能力還不夠吧，但是單單從數學的角度來說，肯定是有這么一個公式。所以我希望將來的某一天，有人可以告訴我它的實例，讓我看到自己的這點努力的成果。