經歷過程溝通聯系促進發展
——《積的變化規律》教學

季仕健

【教學內容】

蘇教版數學四年級下冊第33頁“三位數乘兩位數”例4。

【教學過程】

一、探索規律

1.同一乘法算式中因數與積的變化。

（1）導入：同學們，20×3的積是多少？

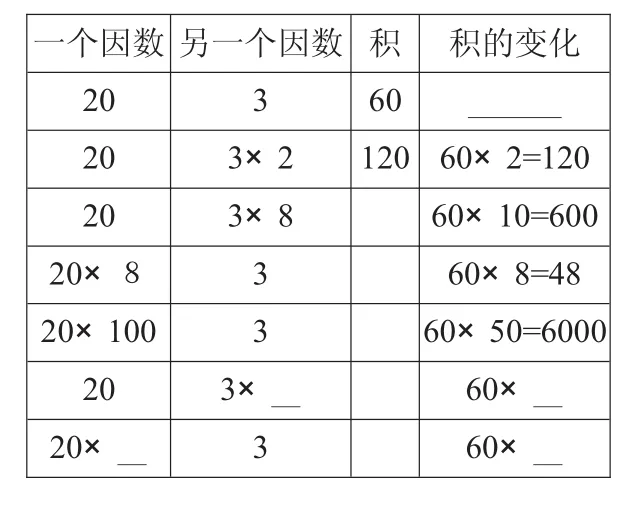
揭示：在20×3=60這個乘法算式中，20是一個因數，3是另一個因數，60是積。

課件：

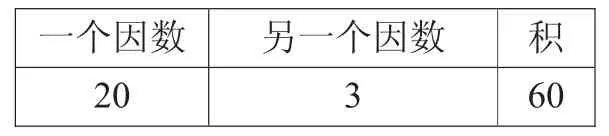
一個因數 另一個因數 積20 3 60

（2）課件：

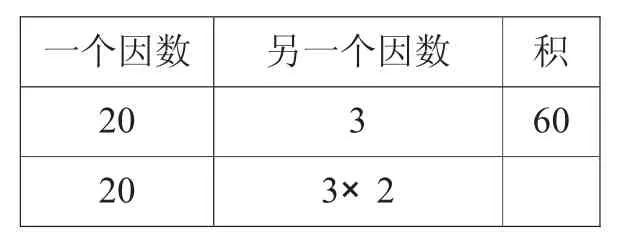
一個因數 另一個因數 積20 3 60 20 3×2

提問：現在20和3這兩個因數發生了怎樣的變化？（板書：一個因數不變，另一個因數乘2，所得的積？）所得的積等于多少呢？你能很快地算出來嗎？

匯報：你是怎么算的？

方法一：20×（3×2）=120；

方法二：60×2=120。

（補充課件：）

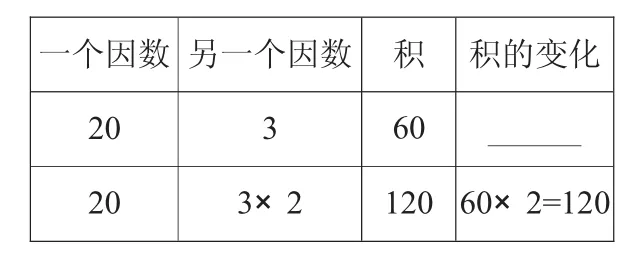
（補充板書：一個因數不變，另一個因數乘2，所得的積等于原來的積乘2）

（3）課件：

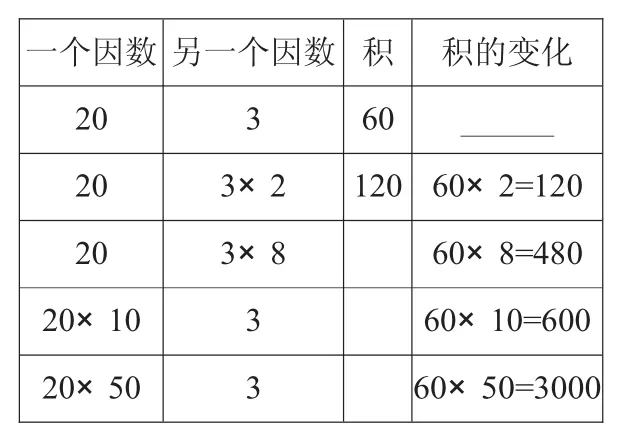
猜測：如果一個因數不變，另一個因數分別乘 8、10、50，所得的積是不是分別等于原來的積乘 8、10、50？

小結：經過驗證，我們發現一個因數不變，另一個因數分別乘 2、8、10、50，所得的積分別等于原來的積乘 2、8、10、50。

拓展：那么，是不是在這個算式中，一個因數不變，另一個因數乘幾，所得的積等于原來的積乘幾？你能不能再自己舉一些例子驗證一下。

課件：

【設計意圖：研究算式20×3=60中，因數20不變，另一個因數3乘2，所得的積等于原來的積乘2，使學生初步感覺到積是變化的。接著讓學生進行猜測，在算式20×3=60中，是不是一個因數不變，另一個因數乘幾，現在的積就等于原來的積乘幾。提出猜想后引發學生探究猜想是否成立，很自然地“逼迫”學生自己進行舉例驗證。在無形中幫學生積累了研究規律的基本經驗。】

2.不同乘法算式中因數與積的變化。

（1）過渡：剛才我們在20×3這個算式中發現了積的變化現象，那么在其他乘法算式中是不是也存在著相同的變化呢？你能不能再自己舉一些例子驗證一下。

探索：

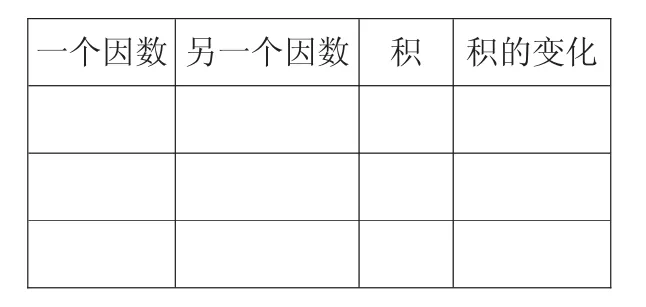
匯報：有沒有不符合這種變化的例子？

（2）總結：經過探索，我們可以發現積的變化規律“一個因數不變，另一個因數乘幾，所得的積等于原來的積乘幾。”

【設計意圖：本環節的教學使學生在交流、互動中傳遞驗證的方法；在對話中感受追尋科學意義驗證方法的迫切需要。這是一個科學嚴謹“做數學”的過程，而不完全歸納的思想恰恰蘊含其中。學生在這一過程中獲得的不是簡單意義上的“規律”，獲得的更是“規律”怎么來的過程，獲得是數學方法的內化。】

二、運用規律

1.規律的鞏固提升。

126×27＝3402

（1）126×（27×19）＝3402×（ ）

（2）（126 ×64）×27 ＝3402×（ ）

（3）126 ×（27 × ） ＝3402×270

（4） （126×△）×54＝3402×（ ）

2.規律的實際應用。

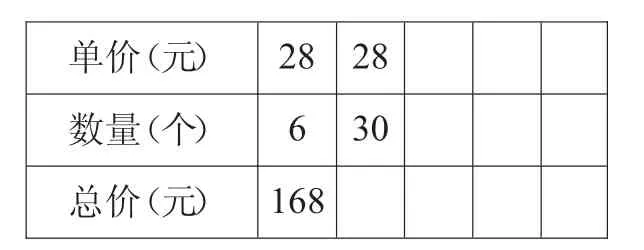
師：一個計算器單價是28元，買6個這樣的計算器要多少元？（168元）

師：買30個計算器呢？怎樣計算？

方法 1：168×5=840。

方法2：直接用28乘30等于840。

師：不運用積的變化規律而直接口算28×30也很容易。如果這種計算器的單價不告訴你（在課件中遮住或隱去題目中“單價是28元”這一個信息），只告訴你買6個這樣的計算器要168元，你能求出買30個計算器要多少元嗎？

一個計算器單價是28元，買6個這樣的計算器要168元，買30個呢？

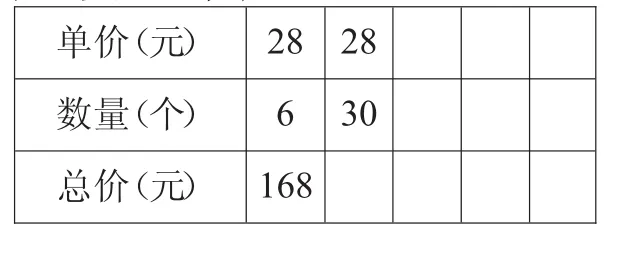
設疑：為什么這里的單價不知道，也能很快地求出后幾列的總價呢？

小結：因為單價×數量＝總價，而這里的單價一直都沒變，也就是一個數不變，另一個數乘幾，積也要乘幾。

【設計意圖：規律的鞏固設計有順向有逆向，從具體的數到抽象的符號，多層次提升了學生的理性思考；規律的實際應用使學生感受到學有所用，提高了學生學習數學的信心與欲望。】

三、溝通聯系

1.溝通規律與口算之間的聯系。

師：其實我們在以前的學習中已經悄悄地用過了積的變化規律，想一想我們是怎樣口算24×30的？能不能用今天所學的知識來解釋呢？

師：這就是可以這樣口算的理由。請你用積的變化規律很快口算出24×300的結果。

師：240×30的乘積與24×300相等嗎？為什么？

2.溝通規律與簡算之間的聯系。

師：你能很快說出18×45的結果嗎？

師：如果老師提供一個參考算式18×5=90，你能很快說出來了嗎？

用課件演示簡算方法：一個因數18不變，另一個因數5乘9，所得的積等于18×5的積90 乘 9，就是 810。

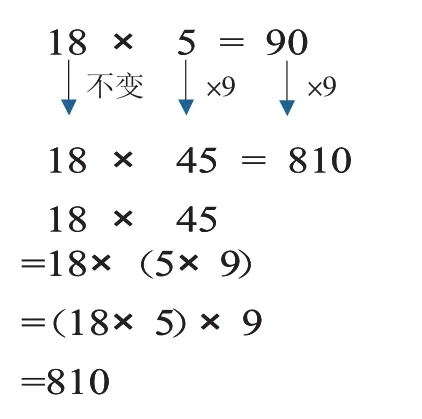
師：這一步“18×（5×9）=（18×5）×9”，你感覺熟悉嗎？運用了什么知識？（乘法結合律）

師：看來，今天學習的積的變化規律和以前學習的乘法結合律也有聯系。用a表示一個因數，b表示另一個因數，積如果用□表示，那么b乘c，就得到 a×（b×c），運用積的變化規律，所得的積等于□乘c，□也就是 a×b，這樣就得到 a×（b×c）=（a×b）×c。

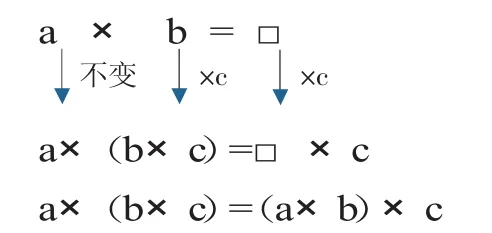
【設計意圖：此處設計溝通了積的變化規律與口算、乘法結合律的聯系，一方面體現了數學內在的統一性；另一方面彌補了規律的舉例驗證中不完全歸納的不足，從乘法結合律的角度對積的變化規律進行了“證明”與溝通。】

四、全課總結

小結：通過今天的學習同學們有了更多的猜想，這些猜想是否正確呢？可以怎么辦？