民用飛機隱蔽故障風險的定量評估方法研究

戴順安，王　燁，蔡　景

(1.中國民航上海航空器適航審定中心，上海　200335； 2.南京航空航天大學，南京　211106)

?

民用飛機隱蔽故障風險的定量評估方法研究

戴順安1，王燁1，蔡景2

(1.中國民航上海航空器適航審定中心，上海200335； 2.南京航空航天大學，南京211106)

摘要：對隱蔽性故障開展風險評估是保持民機持續適航的重要方面，針對隱蔽性故障的特點，結合ARP 5150的風險評估理念，開展了民用飛機隱蔽故障風險的定量評估方法研究，采用帶截尾數據的威布爾分布極大似然估計法，利用實際使用維修數據確定了隱蔽性故障的故障規律；分析了影響隱蔽性故障風險的因素，建立了新的隱蔽故障風險的定量評估方法；最后通過實例，對隱蔽性故障的風險進行定量評估及比較分析，結果表明了本方法的有效性和適用性。

關鍵詞：民用飛機；風險；隱蔽性故障；定量評估

本文引用格式：戴順安，王燁，蔡景.民用飛機隱蔽故障風險的定量評估方法研究[J].兵器裝備工程學報，2016(6):162-165.

Citationformat:DAIShun-an,WANGYe,CAIJing.ResearchonQuantitativeRiskAssessmentMethodforHiddenFailureofCivilAircraft[J].JournalofOrdnanceEquipmentEngineering,2016(6):162-165.

由于飛機空勤組在履行正常職責時，無法發現飛機的隱蔽性故障，因此隱蔽性故障對飛機而言，存在著重大的安全隱患，成為民機關注的焦點[1-3]。為了避免隱蔽性故障的發生，在以ATAMSG-3為指導的維修大綱制定中規定：“必須選擇有效和適用的維修工作，避免隱蔽故障的發生，否則必須重新設計”。對隱蔽故障的重視不僅體現在維修大綱的制定過程中，而且在飛機投入運營后，需持續評估隱蔽故障的風險，在ARP5150的附錄D1.6中對隱蔽性故障進行了解釋，并給出了簡單的定量評估隱蔽性故障風險的例子。例子中假定故障服從指數分布，而且假定每天都進行針對隱蔽故障的“故障發現檢查”(FailureFindingInspection，FFI)。雖然該例子簡單易懂，但滿足以上假定條件的隱蔽故障很少，因此，僅憑ARP5150附錄D1.6中提供的方法，難以在實際持續適航管理中開展針對隱蔽性故障的風險定量評估。

為此，本文以ARP5150附錄D1.6中提供的方法為基礎，結合多年從事持續適航風險評估的經驗，首先利用實際使用的維修數據，確定隱蔽性故障的故障規律；其次，根據隱蔽故障的“故障發現”維修策略，分析影響隱蔽性故障風險的主要因素；最后，建立隱蔽性故障風險的定量評估方法，并進行實例驗證。

1　隱蔽性故障的分布確定

ARP5150附錄D1.6的例子中，假定隱蔽故障服從指數分布。然而，根據美國宇航局統計數據表明，航空設備故障率大致分為6種類型，其中指數分布只占14%。目前在我國的民用飛機可靠性管理中，威布爾分布因能替代指數分布等，具有更強的通用性而被廣泛采用[4-5]。根據比例風險模型(proportionalhazardsmodel,PHM)或健康管理的理念可知，相同部件在不同使用環境下表現出來的故障規律各不相同，甚至差異很大，因此，必須根據部件實際的使用維修數據，擬合得到部件的故障分布參數[6-10]。

在實際的使用維修中，航空公司為了減少隱蔽性故障的風險，通常在實施多次“故障發現檢查”工作后，如未發現故障，就進行預防性更換，這其實就是體現了ATAMSG-3中的“綜合維修”工作的思想。隱蔽性故障的故障發現檢查和預防性更換的時序圖如圖1所示。

從圖1可以看出，部件有的是因失效而更換，這種失效是由檢查發現的，因此部件失效更換的時間不是部件真實的確切失效時間，但兩者非常接近，因此，可以近似為完全數據；而有的部件則是因預防性維修而更換的，屬于右截尾壽命數據[11]。假定收集了n組部件的更換數據，其中r組為完全數據，分別為t(1)≤t(2)≤…≤t(r)，n-r組為右截尾數據，預防性更換時間為tp。

已知兩參數威布爾分布的密度函數[12-13]為

因此，其對應的似然函數為

對上式取對數并求導，再整理簡化后可得：

(1)

這是兩個超越方程，需用數值方法迭代求解，以得到參數m和η。

2　隱蔽性故障風險的定量評估

2.1隱蔽性故障的風險因素分析

根據圖1分析可知，影響隱蔽性故障的發生概率來自兩個方面，已使用時間T，即隨著使用時間的推移，部件的故障率水平就越來越高，因此故障發生概率越來越高；如果檢查間隔τ越大，那么在一個檢查周期內發生故障的概率就越大。但是對于隱蔽性故障而言，故障的發生概率不等于安全風險，安全風險是隱蔽性故障概率與相關故障概率的結合。關于這一點，在ATAMSG-3中進行了詳細描述：隱蔽性故障是否對安全造成影響的判據是“一個隱蔽的功能故障和另一個相關的系統或者備用功能的故障之綜合對使用安全性有直接有害的影響嗎？”，此判據告訴我們，隱蔽性故障本身不會對安全造成影響，只有和其他故障結合了才會造成安全問題。譬如：燃油泄漏是一個隱蔽性故障，但該故障只有和點火源的失效同時發生才能引起火災，燃油泄漏的時間越長引起火災的概率自然就越高。這也就是ARP5150附錄D1.6中所描述的，隱蔽性故障的暴露時間(ExposurePeriod)越長，對應的風險就越大。

因此，對于給定的部件(故障服從參數為m和η的威布爾分布)，已使用時間T、檢查間隔τ、故障暴露時間和相關故障(即和隱蔽性故障結合對安全有害的故障)的失效率λ，共同決定了安全風險。為此，隱蔽性故障的安全風險可以定義為關于m,η,T,τ,λ的函數H(m,η,T,τ,λ)。

2.2隱蔽性故障的風險評估

根據2.1的分析，結合圖1的描述，可知H(m,η,T,τ,λ)由兩大部分構成：隱蔽性故障的發生概率P1，在隱蔽性故障暴露時間內相關故障的發生概率P2。

1) 蔽性故障的發生概率。P1是一個條件概率，即在時間點T之前部件不發生故障的條件下，在[T,T+τ]內發生故障的概率。因此

2) 在隱蔽性故障暴露期間內相關故障的發生概率P2。在[T,T+τ]內的t時刻發生故障，那么隱蔽性故障的暴露時間為T+τ-t，對應的隱蔽性故障暴露時間的期望為

再結合相關故障的失效率λ，因此

綜合以上的分析可得，隱蔽性故障的安全風險H(m,η,T,τ,λ)為

(2)

3　實例分析

某機型燃料管泄漏屬于隱蔽功能系統安全影響類，表1給出了燃料管的漏油失效更換和預防性更換的壽命記錄，單位為飛行小時，其中帶“*”的為預防性更換數據。

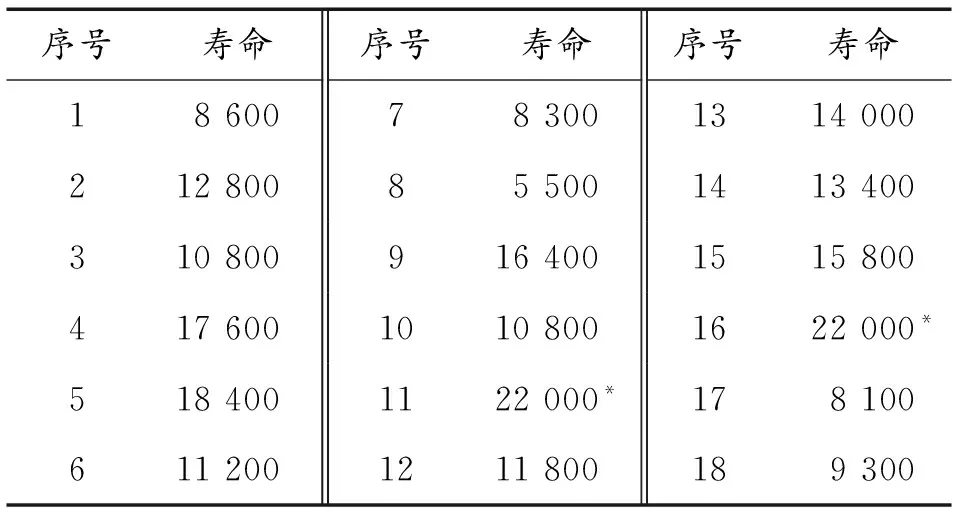
表1　燃料管的壽命數據

采用式(2)，對表1中的壽命數據進行威布爾參數估計，得到m=1.89，η=15 114，如將預防性更換數據簡單的視為失效數據，不采用基于截尾數據的威布爾參數極大似然法，得到參數為m=3.09，η=14 739，是否采用基于截尾的威布爾極大似然法的參數結果比較如圖2所示。

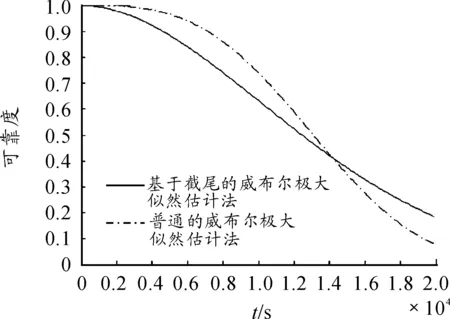
圖2　是否采用基于截尾的威布爾極大似然法的結果比較

根據ARP 5150附錄D1.6中給的實例，假定燃料管泄漏的相關故障點火源的失效率λ=0.000 05，采用式(2)，可得燃料管泄漏在相同檢查間隔τ下的不同使用時刻T的風險的變化，如圖3所示。以及相同使用時刻T下的不同檢查間隔τ的風險變化，如圖4所示。

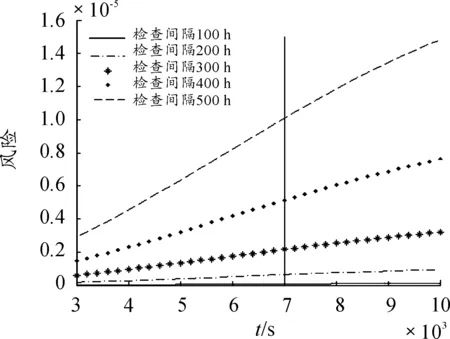
圖3　相同檢查間隔τ下不同使用時刻T的風險

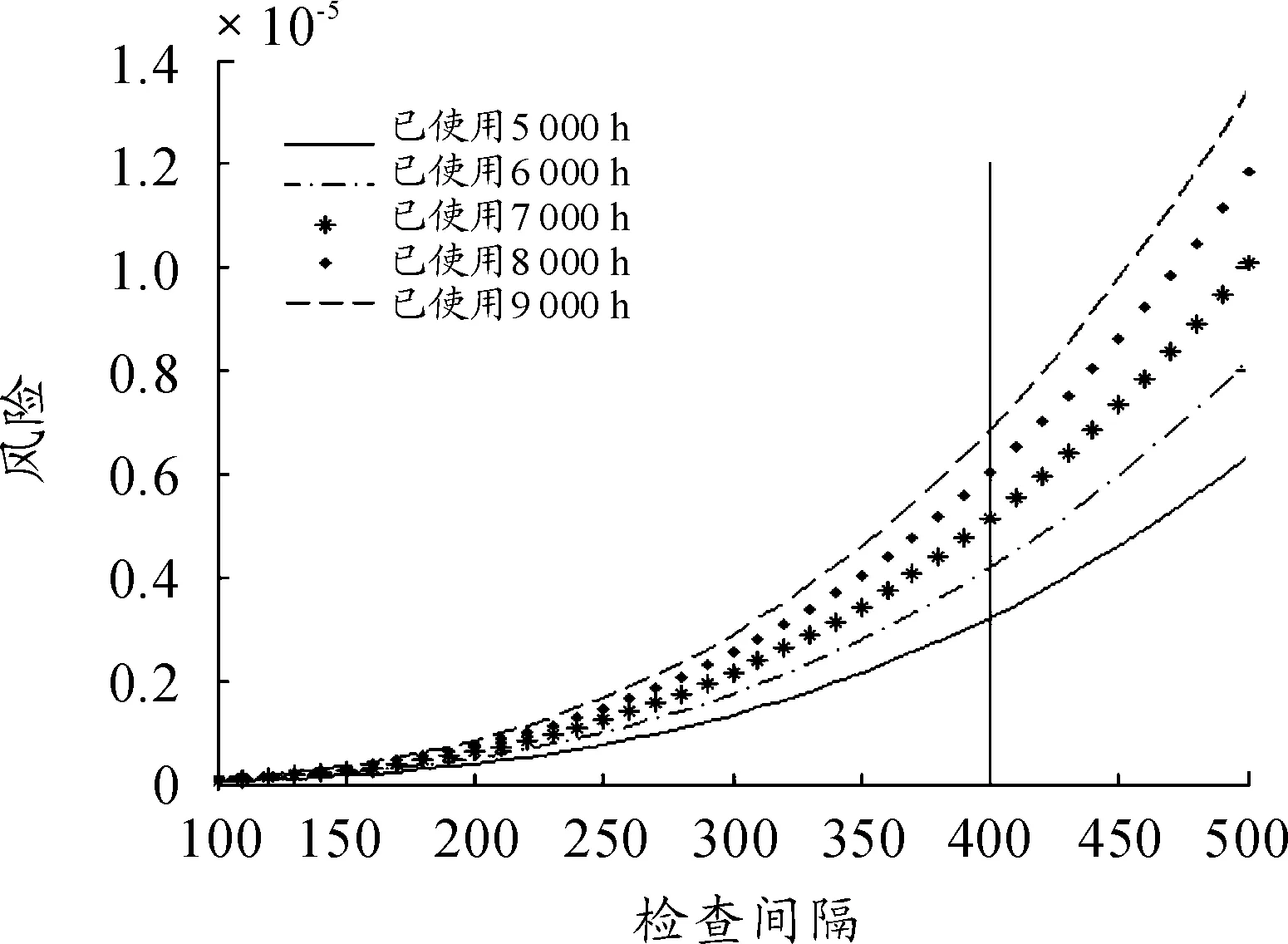
圖4　相同使用時刻T下不同檢查間隔τ的風險

圖3中共有5條曲線，其中曲線“——”代表在不同使用時間，采用500h的檢查間隔的風險。除5條曲線外，圖3中給出了一條豎直線，該豎直線與5條曲線分別相交，從下而上的5個交點，分別表示在T=7 000h時，如檢查間隔分別采用100h、200h、300h、400h、500h的對應風險，風險依次為：7.91×10-8、6.36×10-7、2.16×10-6、5.14×10-6、1.01×10-5。圖4中也有5條曲線，其中曲線“——”代表當使用時間為9 000h時，采用不同檢查間隔的風險。圖4中的豎直線與5條曲線的交點，從下而上分別表示，當使用時間為5 000h、6 000h、7 000h、8 000h、9 000h，如采用400h的檢查間隔所對應風險，風險依次為：3.22×10-6、4.18×10-6、5.14×10-6、6.05×10-6、6.87×10-6。根據圖3、圖4分析可以看出，使用時間越長風險越高，檢查間隔越長風險也越高，這一結果符合故障發生的普遍規律。如果按照ARP5150 附錄D1.6中的方法進行計算的話，那么得到的安全風險是一個定值，不僅不符合燃料管隨著使用時間推移，故障發生概率不斷增加的情況(如圖2所示，不可靠度隨著時間的推移在減低，即故障發生概率在增加)；而且沒有考慮檢查間隔的影響，與實際脫鉤。同時，本文提供的方法可以方便評估在任何時刻采取某種檢查間隔所帶來的定量風險，為快速維修決策，以及確保持續適航提供了有力的手段。

4　結語

民用飛機的隱蔽性故障對飛機構成了重大潛在風險，對隱蔽性故障開展定量風險評估是保持飛機持續適航的重要手段。本文參考APR5150理念，結合實際需求，建立了一種更實用的隱蔽故障風險的定量評估方法，對APR5150中的方法進行了擴充與完善，具有重要的理論意義和實際應用價值。

參考文獻：

[1]蘇義.機載設備隱蔽故障及維修策略[J].航空制造技術，2010(12):86-88.

[2]賈寶惠，劉濤，楊杭，等.民機隱蔽故障維修間隔優化方法研究[J].航空制造技術，2015(S1):20-23.

[3]郭中偉.淺談民用適航管理與航空安全[J].江蘇航空，2014(2):21-22.

[4]LIX,CAIJ,ZUOH.ResearchonReliabilitySequentialComplianceMethodforRollingBearings[J].JournalofInformationandComputationalScience，2015,12(14):5309-5318.

[5]WARDM,MCDONALDN,MORRISONR,etal.APerformanceImprovementCaseStudyinAircraftMaintenanceandItsImplicationsforHazardIdentification[J].Ergonomics，2010,53(2):247-267.

[6]王少萍.大型飛機機載系統預測與健康管理關鍵技術[J].航空學報，2014(6):1459-1472.

[7]于宏軍，韓建軍，張華，等.航空發動機健康管理系統標準探討[J].航空標準化與質量，2012(4):9-11.

[8]楊洲，景博，張劼，等.機載系統故障預測與健康管理驗證與評估方法[J].測控技術，2012(3):101-104.

[9]BAUSSARONJ,MIHAELAB,LéOG,etal.ReliabilityAssessmentBasedonDegradationMeasurements:HowtoCompareSomeModels?[J].ReliabilityEngineering&SystemSafety，2014,131:236-241.

[10]RYANPC,STEWARTMG,SpencerN,etal.ReliabilityAssessmentofPowerPoleInfrastructureIncorporatingDeteriorationandNetworkMaintenance[J].ReliabilityEngineering&SystemSafety，2014,132:261-273.

[11]蔣仁言，胡浩然.對由預防維修活動所產生的截尾數據的初步分析[C].中國運籌學會可靠性分會第九屆可靠性學術會議論文集.長沙:2013136-141.

[12]鄢偉安，宋保維，段桂林，等.威布爾部件的經驗貝葉斯評估[J].系統工程理論與實踐，2013(11):2980-2985.

[13]王繼霞，申培萍.定時截尾下Weibull分布參數估計的EM算法[J].河南師范大學學報(自然科學版)，2009(2):9-11.

(責任編輯楊繼森)

doi:10.11809/scbgxb2016.06.038

收稿日期：2015-12-17；修回日期：2016-01-22

基金項目:民航局重點科技項目(MHDR20150103)

作者簡介：戴順安(1962—)，男，高級工程師，主要從事民用飛機適航審定研究。

中圖分類號：V328

文獻標識碼：A

文章編號：2096-2304(2016)06-0162-04

ResearchonQuantitativeRiskAssessmentMethodforHiddenFailureofCivilAircraft

DAIShun-an1,WANGYe1,CAIJing2

(1.ShanghaiAircraftCertificationCenterofChinaCivilAviation,Shanghai200335,China; 2.NanjingUniversityofAeronauticsandAstronautics,Nanjing211106,China)

Abstract:Risk assessment of hidden failure should be carried out to maintain the continued airworthiness. With the concept of ARP 5150, a quantitative risk assessment method was researched based on the characteristics of hidden failure. A maximum likelihood estimation method with censored data for Weibull distribution was adopted, and the characteristic of hidden failure was determined by maintenance data; The factors affecting the risk of hidden failure were analyzed and quantitative risk assessment method was established. Finally, the method was applied by an example, and the results show the effectiveness and applicability of the proposed method.

Key words:civil aircraft; risk; hidden failure; quantitative assessment