近似公式在航天測控中的應用
倪 興,李曉勇,楊 磊,王旭良,袁小江
(中國衛星海上測控部,江蘇 江陰 214431)
?
近似公式在航天測控中的應用
倪興,李曉勇,楊磊,王旭良,袁小江
(中國衛星海上測控部,江蘇 江陰214431)
摘要:航天測控中,需要避免過于復雜的運算過程,提高計算速度時,常常運用一些近似公式。分析了近似公式的作用、來源,以及在航天測控中的一些應用情況。提出了一種航天測量船實戰使用的簡化的大氣折射修正公式,并對事后使用的精確公式進行了對比分析,結果表明,運用簡化的大氣折射修正公式處理后的數據在定軌精度上滿足要求,同時滿足了實時數據處理對計算速度的要求。
關鍵詞:航天測控;近似公式;大氣折射
本文引用格式:倪興,李曉勇,楊磊,等.近似公式在航天測控中的應用[J].兵器裝備工程學報,2016(6):174-176.
Citation format:NI Xing, LI Xiao-yong,YANG Lei, et al.Application of Approximate Formula on TT&C System[J].Journal of Ordnance Equipment Engineering,2016(6):174-176.
在航天測控中,尤其是在數據處理中,為了獲取高精度的數據,一些數學模型和計算手段比較復雜,處理時間相對較長,但在實時的數據處理中,要求盡可能快地將數據處理完畢,需要避免過于繁復的運算過程,提高計算速度,因此在保證一定精度要求的前提下,應用一些近似公式。有時為了估算或預報某些參數,利用近似公式。
1 近似公式的來源
獲取近似公式,大致有以下幾種方法。
1.1Tailer公式
如果函數f(x)滿足條件:① 在區間[a,b]上有定義;② 在此閉區間上有一直到n階的連續導數f′(x),…,f(n)(x);③ 當a 式中 常用的由Tailer公式而來的近似公式有 這些公式中,x的值越小,則結果越精確。 1.2精確公式的簡化 有些近似公式,是對計算條件做某種近似假設或將精確公式做適當化簡,例如,在計算飛行目標的地面高度時,便需要假設地球是個球形,設地球半徑為a,雷達的測量元素為R、E、A,由幾何關系和余弦定理可得 (a+h)2=a2+R2-2aRcos(90°+E) 對于航天器入軌段或低軌航天器運行段,有h?a,于是得近似公式 (1) 1.3經驗公式 還有一部分近似公式是根據試驗結果或觀測數據擬合的經驗公式,由于試驗結果不可避免含有誤差,因此與試驗曲線對應的經驗公式也都是近似公式。 例如,計算電波折射指數的史密斯—文特勞公式 (2) 便是一個經驗公式。 經驗公式不僅在工程運用上具有實用價值,而且在理論分析上具有一定的價值。建立經驗公式的主要步驟是配置公式類型、決定公式中的系數、對公式進行檢驗3個過程。配置經驗公式,并無一般的通用方法,其具體形式的確定,是根據理論的推斷或從試驗數據變化的趨勢推測而來。常用的決定系數的方法有圖解法、平均法、最小二乘法、相關分析法[2]。檢驗經驗公式時,可將已測知的自變量的值代入函數中,看計算出的函數值與實測值相差多少,若誤差太大,則需對經驗公式適當修改。 近似公式在航天測控中有著廣泛的應用,如用于數據處理、精度分析、實時計算等。 2.1數據處理 數據處理中應用的近似公式很多,如表示三維空間中的旋轉矩陣 (3) 當旋轉角度很小時,由Tailer公式sinα≈α、cosα≈1可得 (4) 其中A是一個反對稱矩陣 (5) 這種極小旋轉坐標變換公式在航天測控中是很多的,如地心固連坐標系與準地心固連坐標系之間的差別是極移的影響,這兩個坐標系之間的轉換矩陣為 (6) 由于極移量很小,于是其轉換矩陣可寫為 (7) 在數據處理中,有時候空間大地直角坐標與大地坐標需要互相轉換,由大地坐標轉換為大地直角坐標的公式是[3] (8) 式中,N,e2為卯酉圈曲率半徑和參考橢球第一偏心率。 而由大地直角坐標轉換為大地坐標的公式是 (9) 從上式的第二式可以知道,大地緯度B的計算公式是一個隱函數,不能直接求解,只能通過迭代法逐步求解。而由近似公式 (10) 式中 (11) (12) (13) (14) 則可以直接求得大地緯度B,經測算,當H<10 km時,公式的精度不低于0.000 01″,對一般數據處理而言,精度已足夠。 2.2精度估計 我國大部分雷達設備是使用極坐標的單站定位體制,主要的測量元素為R、E、A,對陸站而言,其設備位置可以通過大地測量精確獲得,并且固定不變,其定位精度就是測控設備的精度,而航天測量船在海上執行測控任務時是運動的,另外受風、浪、涌的影響,會產生船搖、變形,船載測控設備同樣受此影響,因此,測量船的誤差是測控設備、船搖、變形、船位誤差的合成[4]。即 (15) 式中:σP為總誤差;σPl為雷達位置誤差;σPy為船搖位置誤差;σPb為變形位置誤差;σPw為船位位置誤差。 測量船船位是由慣導系統實時獲得的,精度較低,是海上測量的主要誤差源之一。船位誤差對目標誤差的影響是一種平移偏倚誤差,因地球曲率而被放大,可以用下面的近似公式估計[5] (16) 式中:d站址誤差;D為站址誤差引起的目標位置誤差;Re為地球平均半徑;h為目標高度。由式(1)可得 (17) 船搖姿態誤差和船體變形誤差可以等效成設備的方位和俯仰角誤差,如果存在船體姿態誤差Δkc,Δφc,Δθc,產生的測量設備方位和俯仰角等效誤差為 (18) 于是有 (19) 若縱搖與橫搖等精度測量,即σφc=σθc,由船搖引起的目標位置誤差為 (20) 同樣,由變形引起的目標位置誤差為 (21) 雷達本身的目標位置誤差為 (22) 將式(17)、式(20)、式(21)、式(22)代入式(15)便可得測量船定位精度的近似估計。 2.3實時計算 電波射線在真空中以光速傳播,但在地球上空大氣中傳播時,由于空間各處大氣成分、濕度、溫度、密度和電離程度都不相同,介質特性也極其復雜,因此其傳播速度發生了改變,軌跡也發生了彎曲,因此電波傳播的路徑是曲線,即發生了折射[6-8]。空間目標的定位是用光學或無線電方法確定其方位、仰角、距離,由于大氣折射的影響,折射誤差可以遠大于設備本身的測量誤差,因此,必須修正大氣折射誤差。常用的精度較高的大氣折射修正有射線描跡法、高斯分層法,在航天測量船的實時數據處理中,對時間有嚴格的要求,如果要采用高斯分層法精確修正電波折射,隨著精度的提高和觀測仰角的不同,計算速度將會有所變化,無法滿足實時處理對計算速度的要求,因此采用以下簡化的電波折射誤差修正公式。假設未修正折射誤差的斜距和仰角分別為Re和Ee,而修正電波折射誤差后的觀測量分別為R和E,則電波折射誤差修正量為 ΔR=0.007 16N0cotEe(h/(h+5 000m)) (23) ΔE=N0cotEe(h/(h+10 000 m))10-6 (24) 式中:h為目標離測站地面的高度;N0為測站地面的電波折射指數。 由式(23)、式(24)兩式,則得到電波折射修正后的觀測量為 R=Re-ΔR E=Ee-ΔE 而外測數據事后處理采用的大氣折射修正為高斯分層法,較為復雜,感興趣者可查閱相關資料。分別利用實時簡化修正的處理數據和事后高斯分層修正的處理數據定軌,再與精軌做比較,結果如表1所示。 從統計結果看,事后高斯分層修正后的數據定軌精度略高,但在量級上兩種方法大致相當,而簡化大氣折射修正滿足實時處理對計算速度的要求,因而被廣泛地使用在實時數據處理中。 表1 兩種電波折射修正定軌結果與精軌差異結果統計 近似公式在航天測控中有著廣泛的運用,可以根據實際工作的需要,導出具有一定精度的近似公式,給分析問題帶來方便。 參考文獻: [1]《數學手冊》編寫組.數學手冊[M].北京:高等教育出版社,2009. [2]張普慶.經驗公式的系數計算及類型配置[J].山東師大學報:自然科學版,1987,2(2):158-165. [3]嚴莘稼,曾啟雄.空間大地直角坐標直接結算大地緯度的近似公式[J].北京建筑工程學院學報,1991(2):55-58. [4]倪興,李曉勇,薛國虎,等.測量船姿態誤差影響分析[J].四川兵工學報,2014,35(5):149-151. [5]簡仕龍,費加兵,劉冰,等.航天測量船海上測控技術概論[M].北京:國防工業出版社,2009. [6]劉利生,張玉祥,李杰,等.外彈道測量數據處理[M].北京:國防工業出版社,2002. [7]李輝芬,席震東,薛國虎,等.低仰角大氣折射誤差對初軌精度的影響分析[J].飛行器測控學報,2012,31(3):54-57. [8]張瑜,張潔寒.全國大氣折射率剖面預測方法[J].電光與控制,2011,18(7):46-48. (責任編輯楊繼森) doi:10.11809/scbgxb2016.06.041 收稿日期:2015-12-25;修回日期:2016-01-15 作者簡介:倪興(1976—),男,工程師,主要從事海上測量數據處理與精度分析研究。 中圖分類號:TJ01;V557 文獻標識碼:A 文章編號:2096-2304(2016)06-0174-03 Application of Approximate Formula on TT&C System NI Xing, LI Xiao-yong,YANG Lei, WANG Xu-liang, YUAN Xiao-jiang (China Satellite Maritime Tracking and Controling Department, Jiangyin 214431, China) Abstract:The approximate formula is often adopted to enhance the computation speed and avoid the complicated calculation. We briefly discussed the source and applications of the related approximate formulae in space-tracking engineering. At last, a new method of a simplified formula about atmospheric refraction correction used on TT&C ship was proposed, and then we compared it with an accurate formula used on accurate handling. The result shows that the accuracy of initial orbit based on simplified formula is satisfied and the speed of compute is satisfied. Key words:spaceflight test control; approximate formula; atmospheric refraction2 近似公式在航天測控中的應用
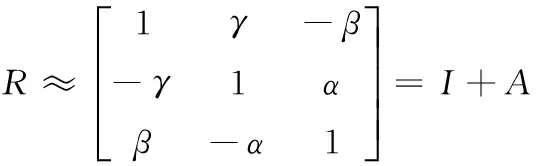
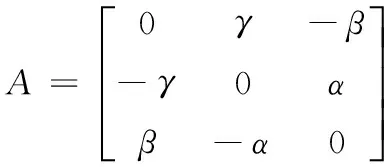

3 結束語

