含輸入時滯的電動汽車懸架系統(tǒng)有限頻域振動控制的研究

陳長征， 王　剛， 于慎波

(1. 沈陽工業(yè)大學 機械工程學院，沈陽　110870； 2. 遼寧省振動噪聲控制技術(shù)工程研究中心，沈陽　110870)

含輸入時滯的電動汽車懸架系統(tǒng)有限頻域振動控制的研究

陳長征1，2， 王剛1， 于慎波1

(1. 沈陽工業(yè)大學 機械工程學院，沈陽110870； 2. 遼寧省振動噪聲控制技術(shù)工程研究中心，沈陽110870)

由于輪轂電機驅(qū)動的電動汽車的驅(qū)動系統(tǒng)安裝在輪轂處，使得汽車懸架系統(tǒng)簧下質(zhì)量增加，造成舒適性變差及電機軸承磨損嚴重等問題。基于上述現(xiàn)象，并綜合考慮控制回路的輸入時滯及參數(shù)攝動因素，研究了該類懸架系統(tǒng)的有限頻域動態(tài)輸出反饋振動控制策略。對比于傳統(tǒng)的時滯全頻域的H∞控制方法，該方法能在人體對振動較為敏感的頻段內(nèi)取得更好的干擾衰減，同時也能保證相關(guān)的時域硬約束。為了降低車身加速度在非簧載模態(tài)頻率處的奇異值，并減少傳遞到電機軸承上的力，考慮將動力吸振器(DVA)安裝在電機軸承座上。通過Lyapunov-Krasovskii泛函及廣義KYP引理，以線性矩陣不等式的形式推導出基于動態(tài)輸出反饋的控制準則。最后，通過一個數(shù)值實例驗證該方法在頻域及時域的有效性。

有限頻域振動控制；主動懸架；輸入時滯；廣義KYP引理；H∞控制

隨著汽車工業(yè)的發(fā)展，以節(jié)能環(huán)保為主題的新能源汽車已經(jīng)成為行業(yè)開發(fā)的主要趨勢，諸如混合動力汽車及純電動汽車等一系列車型。而在純電動汽車當中，基于輪轂電機驅(qū)動的電動汽車具有其獨特的性能優(yōu)勢，除了可精確而快速的控制每個輪的轉(zhuǎn)矩外，還可提高汽車的穩(wěn)定及操縱等運動性能[1]，然而由于其驅(qū)動系統(tǒng)安裝在輪轂處，使得簧下質(zhì)量增加，且電機軸承直接承受著車身的重量，不僅造成舒適性變差，也造成電機軸承磨損嚴重等問題[2]。在路面的干擾下，輪胎傳遞到輪轂軸心的相對位移也會影響到電機的控制精度，諸多問題限制了該類型電動汽車的發(fā)展。由于懸架系統(tǒng)的各性能間存在一定的矛盾關(guān)系，諸如舒適性與懸架動行程及接地性等[3]，研究先進的控制方法來實現(xiàn)汽車懸架的多目標優(yōu)化，一直是近年來的研究熱點。隨著一種考慮約束限制的H∞控制方法的提出，大部分學者都將其應(yīng)用于懸架的振動控制當中[3-6]。該方法能在保證行程約束的情況下，最大化的在全頻域內(nèi)提高懸架的舒適性。然而根據(jù)國際ISO2361標準，人體對4～8 Hz范圍內(nèi)的振動最為敏感，且汽車的舒適性與該范圍內(nèi)的車身振動加速度密切相關(guān)[7-9]，如何將控制目標限定在低頻范圍內(nèi)，以實現(xiàn)懸架性能的權(quán)衡一直是一個難點問題。日本學者Iwasaki等[10]提出了廣義KYP引理，建立了頻域不等式與時域不等式的等價關(guān)系，為實現(xiàn)有限頻域控制提供了一種有效的方法。Sun等[7]應(yīng)用該引理實現(xiàn)了汽車懸架系統(tǒng)的有限頻域多目標控制，結(jié)果表明該方法優(yōu)于傳統(tǒng)的全頻域方法。Zhang[11]將其應(yīng)用于結(jié)構(gòu)抗震控制當中。考慮到在實際的應(yīng)用當中，控制回路不可避免的存在時滯現(xiàn)象，而輸入時滯對系統(tǒng)的性能有很大的影響，甚至會導致控制系統(tǒng)失穩(wěn)[12-14]。因此在設(shè)計懸架系統(tǒng)的控制方法時，輸入時滯是必須要考慮的因素。文獻[12-13]分別針對汽車懸架及座椅懸架設(shè)計了考慮輸入時滯的全頻域狀態(tài)反饋控制器，在一定時滯范圍內(nèi)，取得了很好的減振效果。文獻[9]通過廣義KYP引理提出了處理時滯懸架的有限頻域狀態(tài)反饋控制方法。考慮到全狀態(tài)反饋成本過高，安裝不便等問題，實際應(yīng)用難以實現(xiàn)，文獻[14]提出了基于動態(tài)輸出反饋的時滯全頻域H∞控制方法，結(jié)果表明對于選擇的可測狀態(tài)量，該方法在存在可行解的條件下，滿足一切性能要求。

基于上述分析，有必要研究考慮輸入時滯的輪轂電機驅(qū)動電動汽車主動懸架系統(tǒng)的動態(tài)輸出反饋控制策略。故本文針對該類型的主動懸架模型，結(jié)合動力吸振器，綜合考慮輸入時滯及參數(shù)攝動項，應(yīng)用廣義KYP引理推導出了基于動態(tài)輸出反饋的有限頻域H∞魯棒控制準則，并將其應(yīng)用于該類型電動汽車懸架系統(tǒng)的多目標控制當中，最后通過一個數(shù)值實例驗證了該方法的有效性。

符號標記：PT、PH、P-1分別表示矩陣P的轉(zhuǎn)置、共軛轉(zhuǎn)置、逆，(P)s=P+PT，P?0、P<0表示其分別為正定、負定矩陣，P?Q表示矩陣的克羅內(nèi)克積，*表示矩陣的相應(yīng)對稱塊矩陣，N{·}表示{·}的零空間，n表示n維的復空間，Hn表示n×n維哈密頓矩陣，Sn表示n×n維的實對稱矩陣，diag[·]表示對角矩陣，L2[0∞)表示平方可積的矢量函數(shù)空間。

1問題描述及必要引理

為了便于研究系統(tǒng)的動態(tài)特性，將圖1所示的物理模型簡化為如圖2所示的1/4主動懸架模型。其中ms、md、ma、mu分別代表簧載質(zhì)量、動力吸振器質(zhì)量、懸架臂和剎車部件及電機軸承座的集中質(zhì)量、非簧載質(zhì)量，ks、kd、ka、ku分別為懸架剛度、動力吸振器剛度、輪轂電機軸承處彈性支承的剛度、輪胎剛度，cs、cd為懸架阻尼及動力吸振器阻尼，u(t-d)為含輸入時滯d的主動控制力，xs、xd、xa、xu分別為簧上質(zhì)量的位移、動力吸振器位移、輪轂軸心位移，非簧載質(zhì)量位移，q為路面不平度激勵。

圖1　/4電動汽車主動懸架系統(tǒng)物理模型原理圖Fig.1 Schematic diagram of the physical quarter-car model of electric vehicles active suspension

圖2　基于DVA的主動懸架1/4車模型Fig.2 Quarter vehicle suspension model of an in-wheel motor driven electric vehicle with DVA

這里選取上述懸架系統(tǒng)的狀態(tài)變量為

x(t)=[x1x2x3x4x5x6x7x8]T

(1)

則如圖2所示的主動懸架系統(tǒng)可用如下的狀態(tài)空間方程描述：

(B +ΔB)u(t-d)+B1ω(t)

(2)

其中

這里定義待設(shè)計的全階動態(tài)輸出反饋控制器形式如下：

(3)

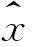
將上述性能指標歸一化并用下式描述為：

(4)

這里z1(t)為系統(tǒng)的控制輸出，代表車身垂直加速度，z2(t)為歸一化的系統(tǒng)約束函數(shù)。其中

M=ms+md+ma+mu

結(jié)合式(2)～(4)，可得：

(5)

其中:

這里要求上述的閉環(huán)系統(tǒng)(5)在干擾能量及時滯有界的情況下滿足：

(6)

為了得到本文的主要結(jié)論，這里首先介紹下列重要的引理。

引理1[11]假定F為實矩陣，Θ為一對稱矩陣，這里定義Φ∈S2、Ψ∈Η2，Λ(Φ,Ψ)為復平面上一條曲線，則下面兩個表述互相等價：

(1) 若s∈Λ(Φ,Ψ)，且對于所有的非零(u,υ)∈NLsF，有

(7)

(2) 對于所有的非零(u,υ)∈NLsF，存在對稱矩陣P，Q>0使得如下不等式成立：

FH(Φ?P+Ψ?Q)F+Θ<0

(8)

引理2[9]對于x∈RnP∈Sn，H∈Rm×n，若H的秩小于n，則下面表述等價：

xTPx<0，?Hx=0，x≠0，

??Y∈Rn×m，P+YH+[YH]T<0

引理3[16]給定對稱矩陣Q及一般矩陣H、R，若Q+HΣR+RTΣTHT<0?ΣΣT≤I，當且僅當存在常數(shù)λ>0，使得Q+λ-1HHT+λRTR<0。

2有限頻域控制結(jié)果

(9)

(10)

(11)

(12)

其中：

證明當ω(t)=0時，考慮如(13)所示的Lyapunov Krasovskii泛函:

(13)

其中P1>0、S1>0、R1>0，對上式求導可得：

這里應(yīng)用Jensen不等式[15]來處理上式中的積分項，則可得

(14)

(15)

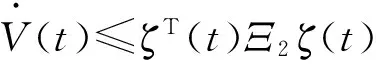
(16)

這里ξ(t)=(ζT(t)ωT(t))T，為了建立頻域不等式，這里將ξ(t)進行傅里葉變換，并根據(jù)Parseval等式[9]可得：

(17)

(18)

應(yīng)用schur補定理可將式(18)轉(zhuǎn)換為式(11)，式(12)形式，故定理1得證。

這里取LMI變換矩陣為：

(19)

將式(19)中的Δ1、Δ2、Δ3、Δ4及其轉(zhuǎn)置分別對式(9)～(12)進行同余變換，并定義如下變量矩陣：

(20)

可得如下推論。

(21)

(22)

(23)

(24)

其中

通過求解推論1，若存在可行解，則通過求解下列等式可唯一的確定控制器參數(shù)矩陣。

3數(shù)值實例分析

為了研究該方法的可行性，將推論1應(yīng)用到含輸入時滯的輪轂電機驅(qū)動電動汽車懸架系統(tǒng)的多目標控制當中，并與文獻[14]中處理時滯的全頻域動態(tài)輸出反饋方法進行比較。總求解目標可歸結(jié)為如式(25)所示的凸優(yōu)化問題。通過內(nèi)點法求解式(25)，可得到懸架系統(tǒng)在有限頻段內(nèi)的次優(yōu)H∞性能指標，相關(guān)的懸架系統(tǒng)仿真參數(shù)見表1。

minγ2

(25)

表1　主動懸架系統(tǒng)參數(shù)

3.1頻域分析

圖3　車身振動加速度奇異值響應(yīng)曲線Fig.3 MSVs response of body acceleration

圖4　(xa-xu)/xaumax的奇異值響應(yīng)曲線Fig.4 MSVs response of (xa-xu)/xaumax

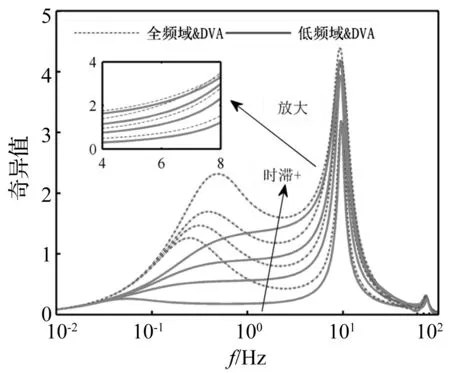
圖5　不同時滯下的加速度頻響Fig.5 Frequency responses of body acceleration for different delay

圖6　不同時滯下的(xa-xu)/xaumax頻響曲線Fig.6 Frequency responses of (xa-xu)/xaumax for different delay

3.2時域分析

為了進一步分析該方法對時域的硬約束響應(yīng)情況，這里選擇的路面輸入為短時的包塊沖擊激勵，其導數(shù)可用如下公式描述[8]：

(26)

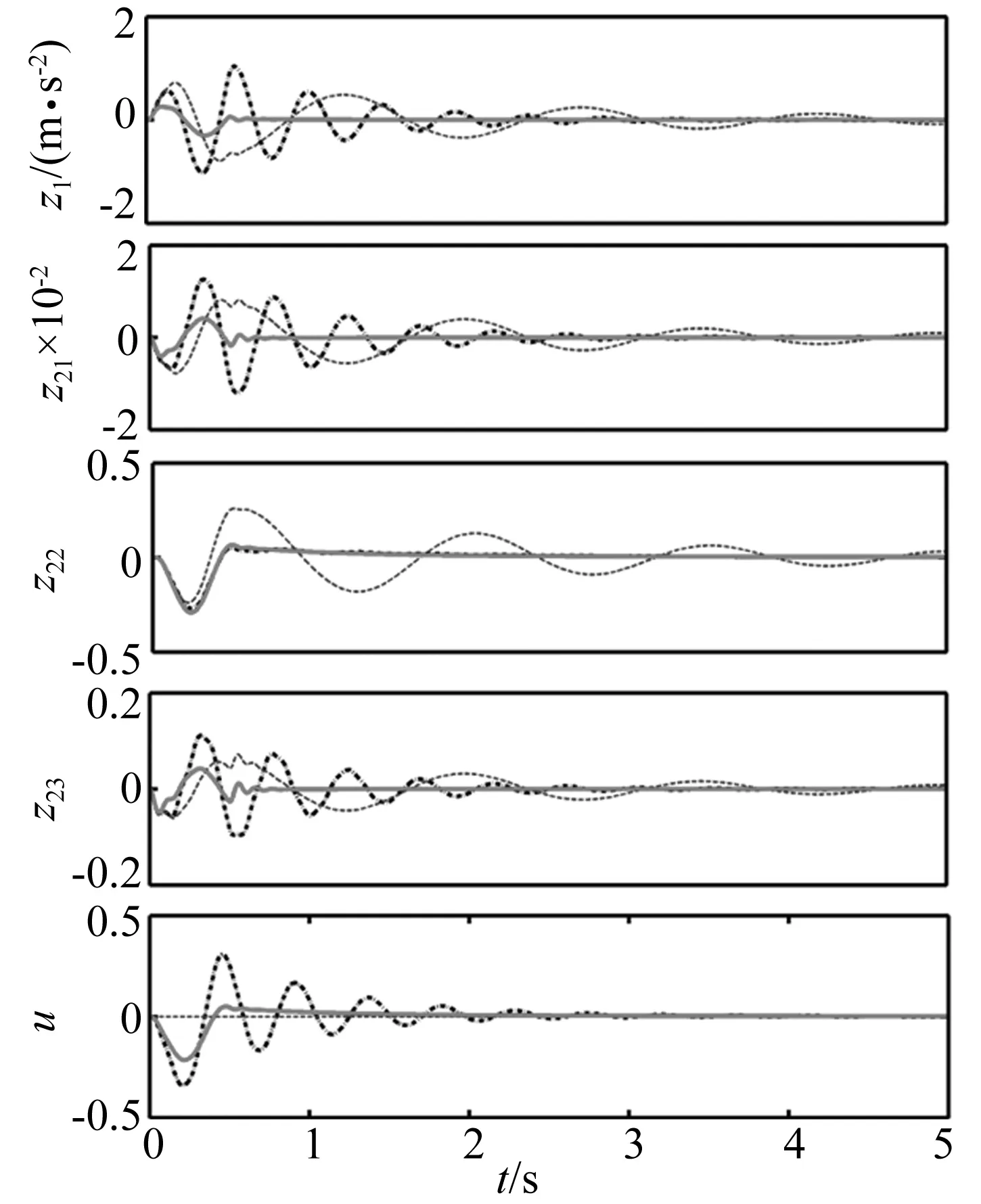
圖7　主動懸架控制輸出包塊時域響應(yīng)Fig.7 Bump response of controlled output for active suspension

(27)

式(27)中選擇激勵時間T=10 s。表中控制器Ⅰ，Ⅱ，Ⅲ分別對應(yīng)低頻域&DVA，全頻域&DVA，無控三種控制方法，從表中可看出，當時滯項依次增大時，在隨機路面激勵下，有限頻域的方法在各項性能指標上依然優(yōu)于傳統(tǒng)的全頻域方法。

表2　加速度均方根值

表3　(xa-xu)/xaumax均方根值

表4　懸架動行程比均方根值

4結(jié)論

本文針對輪轂電機驅(qū)動的電動汽車存在舒適性差及電機軸承磨損和控制精度等問題，研究了在該特定模型下的懸架低頻振動控制策略，且考慮到實際應(yīng)用當中，控制回路含輸入時滯及參數(shù)攝動現(xiàn)象，綜合上述因素，在匹配人體對振動較為敏感的特定頻段內(nèi)，結(jié)合動力吸振器，應(yīng)用廣義Kalman-Yakubovich-Popov (KYP) lemma，以線性矩陣不等式(LMI)的形式推導出基于動態(tài)輸出反饋的有限頻域H∞魯棒控制準則，理論分析與數(shù)值仿真驗證了該方法在頻域及時域的有效性，與傳統(tǒng)的時滯全頻域方法相比，更好的抑制了低頻處的振動，使得舒適性得到了很大的提高，且限制了輪胎傳遞到輪轂軸心的相對位移，為該類型的電動汽車懸架問題提供一種新的解決方案，注意到在該方法中，存在可調(diào)參數(shù)，使得該問題僅能得到次優(yōu)解，如何優(yōu)化可調(diào)參數(shù)得到問題的最優(yōu)解，也是需要考慮的因素。

[ 1 ] Wang R, Chen Y, Feng D, et al. Development and performance characterization of an electric ground vehicle with independently actuated in-wheel motors[J]. Journal of Power Sources, 2011, 196(8): 3962-3971.

[ 2 ] Wang R, Jing H, Yan F, et al. Optimization and finite-frequencyH∞control of active suspensions in in-wheel motor driven electric ground vehicles[J]. Journal of the Franklin Institute, 2015, 352(2): 468-484.

[ 3 ] Chen H, Guo K H. ConstrainedH∞control of active suspensions: an LMI approach[J]. IEEE Transactions on Control Systems Technology, 2005, 13(3): 412-421.

[ 4 ] 李榮, 焦曉紅, 楊超. 基于動態(tài)輸出反饋的半車主動懸架系統(tǒng)魯棒控制[J]. 振動與沖擊，2014, 33(7): 187-193.

LI Rong, JIAO Xiao-hong, YANG Chao. Output feedback-based robust control for a half-car hydraulic active suspension system[J]. Journal of Vibration and Shock, 2014, 33(7): 187-193.

[ 5 ] Li P, Lam J, Cheung K C. Multi-objective control for active vehicle suspension with wheelbase preview[J]. Journal of Sound and Vibration, 2014, 333(21): 5269-5282.

[ 6 ] Guo L X, Zhang L P. RobustH∞control of active vehicle suspension under non-stationary running[J]. Journal of Sound and Vibration, 2012, 331(26): 5824-5837.

[ 7 ] Sun W, Gao H, Kaynak O. Finite frequencyH∞control for vehicle active suspension systems[J]. IEEE Transactions on Control Systems Technology, 2011, 19(2): 416-422.

[ 8 ] Sun W, Li J, Zhao Y, et al. Vibration control for active seat suspension systems via dynamic output feedback with limited frequency characteristic[J]. Mechatronics, 2011, 21(1): 250-260.

[ 9 ] Sun W, Zhao Y, Li J, et al. Active suspension control with frequency band constraints and actuator input delay[J]. IEEE Transactions on Industrial Electronics, 2012, 59(1): 530-537.

[10] Iwasaki T, Hara S. Generalized KYP lemma: unified frequency domain inequalities with design applications[J]. IEEE Transactions on Automatic Control,2005,50(1): 41-59.

[11] Zhang H, Wang R, Wang J, et al. Robust finite frequencyH∞static-output-feedback control with application to vibration active control of structural systems[J]. Mechatronics, 2014, 24(4): 354-366.

[12] Du H, Zhang N.H∞control of active vehicle suspensions with actuator time delay[J]. Journal of Sound and Vibration, 2007, 301(1-2): 236-252.

[13] Zhao Y, Sun W, Gao H. Robust control synthesis for seat suspension systems with actuator saturation and time-varying input delay[J]. Journal of Sound and Vibration,2010,329(21): 4335-4353.

[14] Li H, Jing X, Karimi H. Output-feedback-basedH∞control for vehicle suspension systems with control delay[J]. IEEE Transactions on Industrial Electronics, 2014, 61(1): 436-446.

[15] Ali M S, Saravanakumar R. Novel delay-dependent robustH∞control of uncertain systems with distributed time-varying delays[J]. Applied Mathematics and Computation, 2014, 249: 510-520.

[16] Wu M, He Y, She J H, et al. Delay-dependent criteria for robust stability of time-varying delay systems[J]. Automatica, 2004, 40(8): 1435-1439.

Finite frequency domain vibration control for suspension systems of electric vehicles with actuator input delay

CHEN Chang-zheng1,2, WANG Gang1, YU Shen-bo1

(1. School of Mechanical Engineering, Shenyang University of Technology, Shenyang 110870, China;2. Liaoning Engineering Center for Vibration and Noise Control, Shenyang 110870, China)

For an in-wheel motor driven electric vehicle, its driving system is installed on the wheel hub position and the unsprung mass of the vehicle suspension system increases, they may severely deteriorate the riding comfort and cause problems like severe wear of motor bearings. Considering the above phenomena and the input delay and parametric uncertainties of control loop, the finite frequency domain dynamic output-feedback vibration control strategy for this kind of suspension system was studied. Compared with the traditional entire frequency domainH∞control approach, the proposed approach could achieve a better disturbance attenuation within a frequency band where a human body was more sensitive to vibration. Meanwhile, the related time-domain rigid constraints were also guaranteed. In order to minimize the singular value response of the vehicle body acceleration at the unsprung mass modal frequency and reduce the force transmitted to the motor bearing, a dynamic vibration absorber (DVA) was installed at the motor bearing seat. Using the generalized Kalman-Yakubovich-Popov(KYP) lemma and Lyapunov-Krasovskii functional, the control criterion based on dynamic output-feedback was derived in the form of LMIs. At last, a numerical example was given to verify the effectiveness of the proposed control method in frequency domain and time domain.

finite frequency domain vibration control; active suspensions; input delay; generalized KYP lemma;H∞control

10.13465/j.cnki.jvs.2016.11.020

國家自然科學基金(51175350)

2015-02-28修改稿收到日期：2015-06-04

陳長征 男，博士，教授，博士生導師，1964年生

王剛 男，博士生，1990年生

TP271；O328

A