考慮擺動效應的立式儲罐隔震分析簡化力學模型

孫建剛， 郝進鋒， 劉　揚， 王　振， 崔利富

(1.大連民族大學 土木工程學院,遼寧　大連　116600； 2.蘭州理工大學 土木建筑工程學院,蘭州　730050；3.東北石油大學 土木建筑工程學院,黑龍江　大慶　163318)

考慮擺動效應的立式儲罐隔震分析簡化力學模型

孫建剛1,2， 郝進鋒3， 劉揚3， 王振1， 崔利富1

(1.大連民族大學 土木工程學院,遼寧大連116600； 2.蘭州理工大學 土木建筑工程學院,蘭州730050；3.東北石油大學 土木建筑工程學院,黑龍江大慶163318)

對于基礎隔震大型立式儲罐的地震響應分析問題，考慮土壤與結構的相互作用和儲罐的擺動效應，從流體速度勢理論出發，結合儲罐儲液與罐壁的邊界條件，建立液體運動勢函數和相應的基底剪力、傾覆力矩及波高的理論表達式；并依據剪力和彎矩等效的原理，建立了具有擺動效應的基礎隔震儲罐的力學簡化模型，利用能量原理建立了考慮擺動效應的立式儲罐隔震體系的運動方程。同時，以15萬m3大型儲罐為例，進行了減震效應數值計算分析，并與無擺動效應的隔震體系的簡化力學模型進行了比較分析。結果表明：大型儲罐采用基底隔震裝置，可以有效地降低儲罐的基底剪力，對液體晃動波高的控制效果較差，建議在高烈度區，滿足晃動波高的前提下，儲罐上部結構可以降低烈度進行設計。

儲罐; 擺動; 隔震; 地震響應

儲罐震害調查表明：儲罐在地震中常出現“象足”式破壞、底角焊縫撕裂、儲液泄漏、甚至造成火災、爆炸和環境污染等[1-3]，為降低儲罐的地震響應，儲罐基礎可采用隔震措施。儲罐抗震及隔震設計時，一般將罐體液體分為與罐壁一起運動的剛性脈沖質量、罐壁與液體的液固耦合質量和液體晃動質量三部分，僅考慮上述三質點的水平運動，而不考慮罐體的擺動效應，建立體系的力學運動方程，由此進行儲罐的隔震設計。但是工程中，儲罐在地震作用下，儲液、基礎、地基、隔震裝置和罐體等作為一個整體系統而隨地震波一起運動，除了水平運動外，儲罐系統還可能產生擺動。鑒于此，本文主要考慮儲罐的擺動效應，依據速度勢理論，建立基礎隔震的大型立式儲罐的簡化力學模型和運動方程；選取15萬m3立式儲罐，采用時程分析方法研究大型儲罐地震作用下的隔震效果，并與不考慮擺動效應的基礎隔震儲罐進行對比分析。

1基本假定

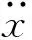
圖1　儲罐幾何坐標系統Fig.1 Geometric coordinate system of tank

2浮頂儲罐的速度勢

根據上述假定和流體力學知識，儲液的速度勢Φ(r,θ,z,t)應滿足如下的Laplace方程和邊界條件：

(1)

(2a)

(2b)

(2c)

(2d)

Φ(r,θ,z,t)=φ1(r,θ,z,t)+

φ2(r,θ,z,t)+φ3(r,θ,z,t)

(3)

2.1剛性速度勢φ1(r,θ,z,t)

(4)

2.2液固耦聯速度勢φ2(r,θ,z,t)

立式鋼制儲罐在振動中，可將罐壁簡化為梁式結構進行簡化分析[3]。在側向力作用下，梁式結構只能激發梁式振型，而不會出現環向振型。由儲罐產生的彈性變形w(z,t)cosθ引發的速度勢φ2(r,θ,z,t)應滿足Laplace方程式(1)；采用分離變量法，利用邊界條件式(2)，把φ2(r,θ,z,t)表示為：

圖2　kn隨n的變化趨勢Fig.2Variation trend of kn-n

2.3對流晃動速度勢φ3(r,θ,z,t)

一般情況下，地震的卓越周期比儲液晃動的自振周期小很多，研究對流晃動時，可近似地認為地面運動為脈沖形式，從而可以忽略表面重力波的影響；但是，當地震波譜中長周期成分占有很大優勢時，則不能忽略表面波的影響；此外，采用基礎隔震體系后，結構基本周期延長，此時也不能忽略表面波的影響，否則將引起較大的誤差。對流晃動速度勢φ3(r,θ,z,t)是由于在φ1(r,θ,z,t)和φ2(r,θ,z,t)作用下壓力不平衡產生的速度勢，根據Laplace方程，采用分離變量法，利用邊界條件可得：

φ3(r,θ,z,t)=

(6)

則總速度勢：

(7)

由總速度勢Φ所產生的儲液中任意一點的動液壓力滿足線性Bernoulli方程，從而可以得到作用于罐側壁(即r=R)上的動液壓力為：

(8)

作用在浮頂上的動水壓力：

(9)

儲液的晃動波高：

(10)

3簡化力學模型及運動方程建立

為建立浮頂儲罐隔震分析的簡化分析力學模型，首先研究在外激勵作用下罐壁和底板上所作用的剪力和彎矩。當有外激勵時，基礎隔震立式儲罐的基底剪力就是作用于罐側壁上沿罐壁高度的動液壓力的合力，可以通過對罐壁的動液壓力進行積分確定[14]：

(11)

作用于罐壁側板上的動液壓力產生的傾覆力矩，可表達為：

(12)

根據儲液系統的動能與等效質點的動能相等的原則，將罐壁運動w(t)轉化為液固耦合質點的運動，即：

(13)

式中：

ML=ρLπR2H，β1=1，

β7=

(14)

式(14)和式(15)可以簡化為如圖3所示的簡化力學模型。內部液體簡化為對流質量mc、脈沖液固耦聯質量mi和剛性質量m0的三質點模型；對流質量和液固耦合質量通過等效彈簧與儲罐罐體相連接，等效彈簧的剛度分別為kc、ki，阻尼常數分別為cc、ci；剛性質量隨罐壁一起運動。地基簡化為具有剛度kα和阻尼cα的轉動彈簧。隔震裝置剛度和阻尼分別為k0和c0。mb1和mb2分別為隔震層的上下墊梁的質量。基礎滑移位移、液固耦聯位移、對流晃動位移、地面運動位移分別用x0(t)、xi(t)、xc(t)和xg(t)表示。

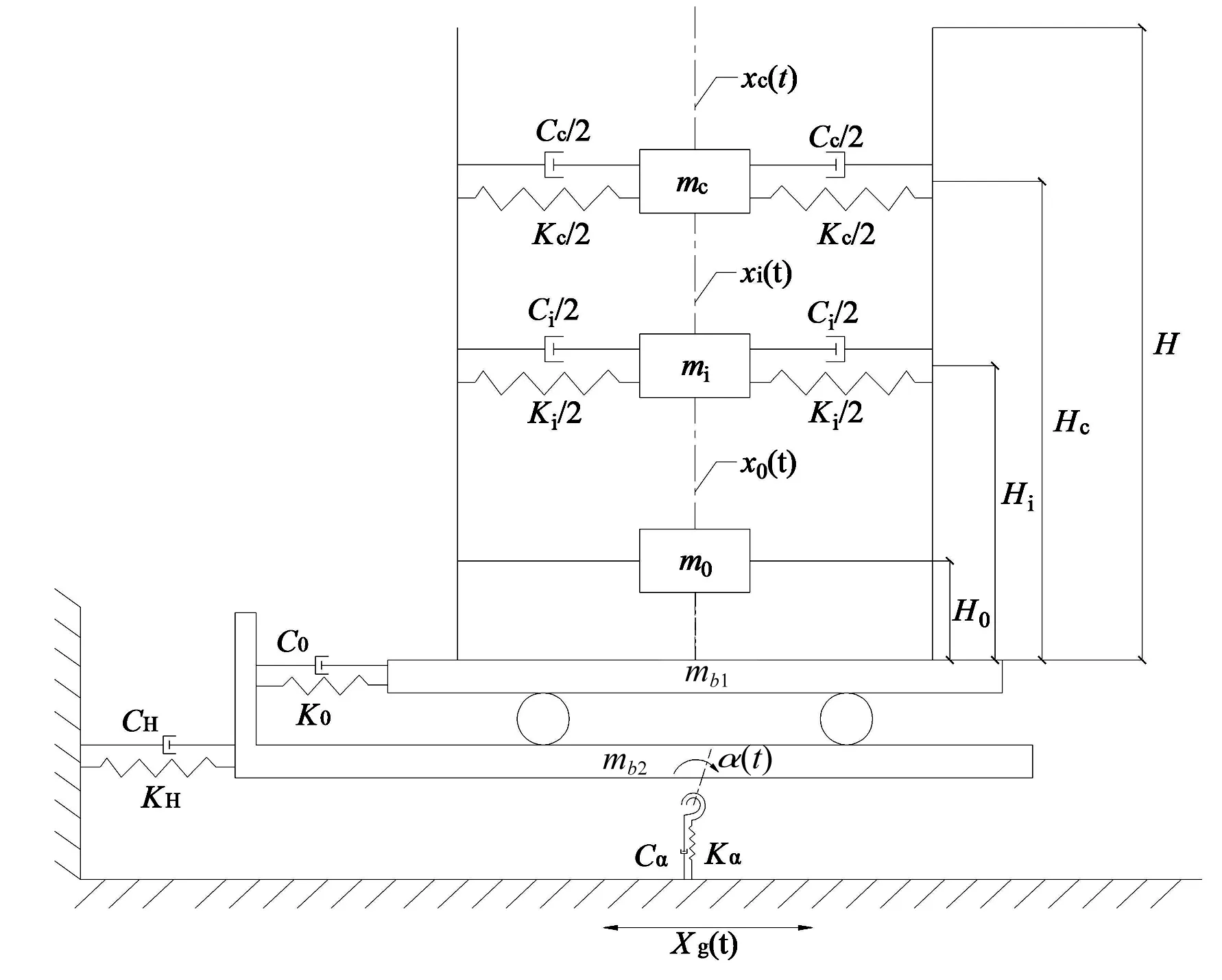
圖3　考慮轉動的基礎隔震浮頂儲罐簡化力學模型Fig.3 Mechanics model of floating roof base isolation tank with the rotation

圖3中晃動剛度由浮頂板的振動方程確定，忽略阻尼項的影響[4]，由浮頂板的振動與液體晃動的協調關系，可得：

(16)

圖3中的k0，c0為隔震層的剛度和阻尼，可由工程設計的隔震周期按單質點體系確定。一般在隔震裝置中加入高阻尼材料，隔震層的阻尼比ζ0可取0.1～0.3。

地基運動可簡化為平動和擺動兩種運動，其水平剛度kH和阻尼cH，轉動剛度kα和阻尼cα等參數按文獻[6]確定：

由文獻[6]可知，場地土類別不同，場地的剪切波速也不相同。關于大于9度地區的石油化工鋼制設備抗震設計，由于缺乏相關地震資料和數據，結合儲罐設備的特點，不考慮土的塑性變形，仍按現行規范進行理論分析；對于座落在不同場地土上的大型儲罐，其儲罐的地震響應可以按照現行的抗震規范確定，主要有與場地土的特征周期有關；若按照時程分析時，可以考慮場地土的水平剛度kH和阻尼cH，轉動剛度kα和阻尼cα隨著場地土的剪切波速而變化，這也反映了場地土對儲罐地震響應的影響。

從圖3的力學模型中，各質量點的質量和高度等參數隨著儲罐徑高比R/H的變化曲線見圖4和圖5。

圖4　各質量點隨徑高比的變化Fig.4 Quality varies with the ratio of D/H

圖5　各質量點高度隨徑高比的變化Fig.5 Quality varies with the ratio of D/H

從圖4和圖5中可見，各質點參數的變化僅與D/H相關，當徑高比加大時晃動質點和剛性質點的質量減小，液固耦聯質點的質量增加，這說明：當儲罐為矮胖罐時，短周期的液固耦聯振動項占主導作用；對于細高罐，晃動沖擊項的慣性作用較大。等效質點的高度隨徑高比的加大而降低，但是當徑高比D/H大于3.0時，液固耦合質點的高度變化不大，趨近于0.45H，這也和我國及日本、美國等有關儲罐地震基底彎矩計算時，脈沖壓力作用的中心高度取液體深度的0.45倍是一致的。

針對簡化分析力學模型，將其視為線性隔震系統時，利用Hamilton原理得出體系相應的運動方程：

(17)

4數值分析

4.1基本參數

以15萬m3儲罐為例，研究儲罐的隔震效果。15萬m3儲罐的基本參數：儲罐直徑D=96.0 m，罐壁高度L=22.8 m，儲液高度H=21.0 m，底圈壁板厚度t1=40.0 mm，罐底邊緣板厚度tb=23.0 mm，鋼材采用日本生產的SPV490。基礎隔震裝置按隔震周期T=3 s進行考慮，隔震裝置的阻尼比取ξ0=0.1。

地基土壤天然密度統一取1 700 kg/m3，土壤泊松比ν=0.3。不同場地土的剪切波速取自文獻[5]，按照推薦的剪切波速值的平均值確定，具體數值見表1。

表1　　建筑場地的剪切波速

4.2自振特性

利用式(17)的質量陣和剛度陣，由特征方程即可得到考慮擺動效應的儲罐結構的自振周期，并與文獻[4]中不考慮擺動效應的儲罐的自振周期和石油化工鋼制設備抗震設計規范(GB50761-2012，以下簡稱規范GB50761)計算結果進行對比分析，具體結果見表2。

表2　　15萬m3儲罐自振周期

由表2 可知，隔震儲罐的液固耦合周期較非隔震儲罐的液固耦合周期明顯拉長，由0.562 s～0.801 s拉長到1.581 s～1.599 s(周期拉長了1.996倍～2.833倍)，即對應于地震加速度反應譜曲線由高峰平臺段向右移動到衰減下降段，地震影響系數的降低而使儲罐的水平地震作用隨之降低；隔震儲罐的晃動周期與非隔震儲罐的晃動周期相接近，變化幅度在3.16%以內，也就是說隔震裝置對控制液體晃動波高效果較差。

規范算法計算結果與非隔震儲罐進行對比分析可知：① 液固耦合周期對比分析，規范算法所得結果與本文及文獻[4]所計算的Ⅰ類場地、Ⅱ類場地、Ⅲ類場地上非隔震儲罐的計算結果相接近，而與Ⅳ場地上非隔震儲罐的計算結果差異較大，誤差達到43.8%，這可能是與儲罐對建造場地要求較高而規范主要考慮堅硬場地土有關，建議儲罐設計時，液固耦合周期應考慮場地土的影響；② 液體晃動周期對比分析，規范算法所得的晃動周期與考慮擺動效應的非隔震儲罐計算結果非常接近，誤差在0.3%以下，而與不考慮擺動效益的非隔震儲罐的晃動周期差異較大，誤差達到18%，這說明規范給出的計算自振特性的公式是考慮儲罐的擺動效應，建議在儲罐的抗震設計中，除考慮儲罐的平動外，還應考慮儲罐的擺動效應。

場地土類別對于隔震儲罐的自振特性影響較小，這主要是因為隔震裝置較柔，隔震儲罐的振動主要集中在隔震層位置；但是場地土類別對于非隔震儲罐的液固耦合周期影響較大，特別是在Ⅳ場地土上儲罐的液固耦合周期明顯增大，且與規范GB50761算法所得結果相差43.8%，所以對于非隔震儲罐的液固耦合周期應考慮場地土的影響。

4.3地震響應

鑒于反應譜理論只反映了地震動的振幅(地震影響系數最大值)和頻譜(周期、振型等)兩個要素，始終不能反映地震動持續時間對結構破壞程度的重要影響。為有效地反映地震動輸入過程中儲罐結構各個時刻的地震響應，本文利用Matlab編寫程序，每類場地分別輸入三條不同地震波，考慮Ⅸ度設防烈度，計算用地震波加速度峰值取0.4 g，采用Wilson-θ法進行時程分析，得出儲罐在四類不同地震波(或場地)作用下的基底剪力和晃動波高等地震響應。因基底彎矩響應時程曲線與基底剪力響應時程曲線基本一致，為節省篇幅，本文僅給出了15萬m3儲罐在考慮擺動時，在金門地震波(Ⅰ類場地)、外交公寓地震波(Ⅱ類場地)、El Centro地震波(Ⅲ類場地)和Pasadena地震波(Ⅳ類場地)作用下的基底剪力和晃動波高的時程曲線，其地震響應時程曲線見圖6；在其它地震波作用下，儲罐的基底剪力、基底彎矩和晃動波高等地震響應的最大值見表3。

圖6　15萬m3儲罐地震響應時程曲線(考慮擺動)Fig.6 Earthquake response time curves of 150 000 m3 tank(Swing)

計算內容場地類別地震波Ⅰ類場地金門Mendocino帝王谷Ⅱ類場地外交公寓CedarhillNorthridge忽略擺動影響非隔震8.5317×1071.0332×1082.6895×1074.9684×1081.1378×1082.8566×107基底剪力Q/N隔震1.7827×1074.1106×1071.6294×1081.0639×1081.2659×1072.3541×108減震率%79.1060.2183.4978.5988.8787.87非隔震8.0525×1081.0142×1092.4069×1084.6694×1091.1522×1092.4043×108基底彎矩M/(N·m)隔震2.0021×1083.7549×1081.5433×1099.1590×1081.4427×1082.2520×109減震率%75.1462.9884.4080.3887.4889.32非隔震0.3130.2830.5680.3640.0170.164晃動波高hv/m隔震0.2910.2670.6090.3790.0070.163減震率%7.035.8276.628-4.1258.680-0.735考慮擺動影響非隔震8.6909×1071.0452×1082.6530×1075.0113×1081.1235×1082.9451×107基底剪力Q/N隔震1.7087×1074.1054×1071.6545×1081.0946×1081.2698×1072.3566×108減震率%80.3460.7283.9778.1688.7087.50非隔震8.2472×1081.0298×1092.3528×1084.7275×1091.1452×1092.4852×108基底彎矩M/(N·m)隔震1.9616×1083.7447×1081.5737×1099.5145×1081.4520×1082.2744×109減震率%76.7263.6485.0579.8787.3289.07非隔震0.1900.1880.3640.1830.0120.105晃動波高hv/m隔震0.1870.1800.3810.2640.0050.107減震率%1.584.4804.612-44.2660.8391.383考慮和忽略擺動影響的對比分析基底剪力誤差%非隔震1.871.16-1.360.86-1.263.10隔震-4.15-0.131.542.890.310.11基底彎矩誤差%非隔震2.421.54-2.251.24-0.613.36隔震-2.02-0.271.973.880.640.99晃動波高誤差%非隔震-39.30-33.57-35.92-49.73-29.41-35.98隔震-35.74-32.58-37.44-30.34-28.57-34.36計算內容場地類別地震波Ⅲ類場地ElCentro波CanogaparkElMonteⅣ類場地Pasadena波金銀島天津波忽略擺動影響非隔震3.3520×1083.2307×1084.9684×1083.7407×1082.7453×1081.9703×108基底剪力Q/N隔震5.6997×1077.0799×1071.0639×1081.9702×1081.7254×1084.1095×107減震率%83.0078.0978.5947.3337.1579.14非隔震3.3074×1093.0795×1094.6694×1093.3622×1092.4128×1091.9779×109基底彎矩M/(N·m)隔震4.8453×1086.0141×1089.1590×1081.6650×1091.4581×1093.6941×108減震率%85.3580.4780.3850.4839.5781.32非隔震0.8960.3950.3640.8470.2950.168晃動波高hv/m隔震0.8950.4530.3790.7400.4150.160減震率%0.11-14.815-4.1212.633-40.5104.551考慮擺動影響非隔震3.3013×1083.2141×1085.0113×1083.6773×1082.7546×1081.9543×108基底剪力Q/N隔震5.9941×1077.5554×1071.0946×1082.0443×1081.7536×1084.1990×107減震率%81.8476.4978.1644.4136.3478.51非隔震3.2910×1093.0989×1094.7275×1093.3666×1092.4641×1091.9909×109基底彎矩M/(N·m)隔震5.2198×1086.4849×1089.5145×1081.7575×1091.5036×1093.8347×108減震率%84.1479.0779.8747.8038.9880.74非隔震0.6080.2900.1830.3850.1980.112晃動波高hv/m隔震0.6020.3010.2640.4630.2800.117減震率%0.99-3.848-44.26-20.079-41.892-4.667考慮和忽略擺動影響的對比分析基底剪力誤差%非隔震-1.51-0.510.86-1.690.34-0.81隔震5.176.722.893.761.632.18基底彎矩誤差%非隔震-0.500.631.240.132.130.66隔震7.737.833.885.563.123.81晃動波高誤差%非隔震-32.14-26.58-49.73-54.55-32.88-33.33隔震-32.74-33.55-30.34-37.43-32.53-26.88

由表3和圖6分析可知，不同地震波輸入下(或不同場地上)的隔震儲罐的減震效果不同。采取隔震措施后，基底剪力的減震效果明顯，而波高的控制效果較差，甚至有放大波高的效應。

由圖6和表3可以看出，采取隔震措施后，對于四種不同種類場地土地震波輸入時，儲罐基底剪力和基底彎矩的隔震效果明顯；由表3計算結果可知：隔震后基底剪力和基底彎矩與隔震前的基底剪力和基底彎矩相比，在堅硬場地土(Ⅰ類場地、Ⅱ類場地、Ⅲ類場地)上的減震效果明顯好于軟弱場地IV類場地)土的減震效果，其減震率達62%以上；對于Ⅳ類場地(軟土)土，隔震儲罐的基底剪力和基底彎矩的也有明顯的減震效果，其減震率也可以達到40%以上。

由表3時程分析計算結果可知，儲罐的基底剪力在考慮地基基礎擺動和不考慮地基基礎擺動兩種情況下，基底剪力最大誤差在7.62%，基底彎矩的最大誤差在7.83%，基本可以滿足工程設計的要求，所以在基底剪力和基底彎矩計算時，可以不考慮基礎擺動的影響；但是對液體的晃動波高來說，考慮擺動影響比不考慮擺動影響時，最大晃動波高一般相差較大，最大晃動波高相差20%～55%，這也與文獻[13]中給出的波高計算公式考慮長周期反應譜調整系數影響相一致，建議儲罐設計時，應考慮儲罐的擺動影響。

對于晃動波高的減震效果分析，不同場地土上隔震儲罐的減震效果差異較大，有時隔震對晃動波高有放大效應。在外交公寓地震波(Ⅱ類場地)和金銀島地震波(Ⅳ類場地)作用下，基礎隔震儲罐的晃動波高較非隔震儲罐的晃動響應明顯增加，隔震后晃動波高較隔震前的晃動波高增加了40%以上；而其他地震波作用時，基礎隔震儲罐的晃動波高與非隔震儲罐的晃動波高相比變化不大。

總之，隔震儲罐比傳統非隔震儲罐的基底剪力明顯降低，由結構抗震知識可知，當隔震后減震率在75%時，相當于抗震烈度降低2度，當隔震后減震率在50%時，相當于抗震烈度降低1度。綜上分析，建議在高烈度地區建造儲罐保證液體晃動波高的要求下，可以采用基礎隔震，采用降烈度設計。

5結論

(1) 依據速度勢理論，考慮地基土壤與結構的相互作用及其儲罐擺動效應的影響，建立了考慮擺動效應的基礎隔震立式儲罐的地震響應分析簡化力學模型。

(2) 考慮擺動影響的非隔震儲罐液體晃動周期與規范計算結果吻合程度較好，說明規范GB50761給出的公式考慮了儲罐擺動的影響，但是沒有考慮場地土類別的影響；場地土類型對儲罐的液固耦合周期影響較大，建議在儲罐抗震設計中，應考慮不同場地土類別的影響。

(3) 采用基礎隔震后，液固耦合周期較非隔震儲罐的自振周期明顯增長，而隔震前與隔震后的液體晃動周期相比變化不大。

(4) 時程分析結果表明，隔震可有效地降低儲罐的基底剪力，且隔震儲罐在堅硬場地上的減震效果好于軟弱場地上的減震效果，在工程設計中可以采用降烈度設計，一般堅硬場地土的隔震儲罐的地震作用可以按降低1度～2度考慮，軟弱場地土上的隔震儲罐的地震作用可以按降低0.5度～1度設計。

[ 1 ] 孫建剛. 大型立式儲罐隔震——理論、方法及實驗[M].北京：科學出版社，2009，12.

[ 2 ] 土木學會新瀉震害調查委員會.新瀉地震震害調查報告[R].東京：土木學會新瀉震害調查委員會1966：1-20.

[ 3 ] 孫建剛. 立式儲罐動響應若干問題研究[D]．哈爾濱：哈爾濱工程大學，2005．

[ 4 ] 孫建剛，崔利富，郝進鋒,等. 考慮浮頂影響的隔震儲罐簡化力學模型及地震響應[J].哈爾濱工業大學學報, 2013,45(10):118-122.

SUN Jian-gang,CUI Li-fu,HAO Jin-feng, et al.The simplified mechanical model and the seismic response for isolation tank with floating roof[J]. Journal of Harbin Institute of Technology，2013,45(10):118-122.

[ 5 ] (GB50011-2010).中華人民共和國國家標準，建筑抗震設計規范[S].北京：中國建筑工業出版社,2010,8.

[ 6 ] Haroun M A. Parametric study of seismic soil-tank interaction. I: horizontal excitation[J]. Journal of Engineering Mechanics, ASCE, 1992, 118(3): 783-797.

[ 7 ] 郝進鋒，孫建剛，劉揚，等. 15萬m3儲油罐樁基礎的隔震設計[J]. 地震工程與工程振動，2014,34 (2):233-239.

HAO Jin-feng, SUN Jian-gang, LIU Yang, et al. Seismic isolation design of 150 000 m3tank pile foundation[J]. Earthquake Engineering and Engineering Vibration， 2014,34(2): 233-239.

[ 8 ] 孫建剛,郝進鋒,王振.儲罐基底隔震振型分解反應譜計算分析研究[J]. 哈爾濱工業大學學報,2005,37(5):649-651.

SUN Jian-gang, HAO Jin-feng, WANG Zhen.Research on the calculation of the mode analysis response spectrum of the seismic base isolation steel storage tank[J]. Journal of Harbin Institute of Technology，2005,37(5):649-651.

[ 9 ] 孫建剛,崔利富,鄭建華.大型全容式 LNG 儲罐基礎隔震地震響應分析[J]. 哈爾濱工業大學學報, 2012,44(8):136-142.

SUN Jian-gang, CUI Li-fu, ZHENG Jian-hua.Seismic response of large-scale full capacity LNG storage tanks with base isolation[J]. Journal of Harbin Institute of Technology，2012,44(8):136-142.

[10] 孫穎,孫建剛,崔利富,等.大型立式浮頂儲罐基礎隔震數值研究[J]. 世界地震工程,2011,27(3):121-123.

SUN Ying, SUN Jian-gang, CUI Li-fu, et al. Numerical research on large base isolation vertical storage tanks with floating roof[J].Word Earthquake Engineering,2011,27(3):121-123.

[11] 孫建剛,崔利富,張營,等.土與結構相互作用對儲罐地震響應的影響[J].地震工程與工程振動，2010,30 (3):141-146.

SUN Jian-gang, CUI Li-fu, ZHANG Ying, et al.Research on seismic responses of storage-tanks considering soil-structure interaction[J]. Earthquake Engineering and Engineering Vibration， 2010,30(3): 141-146.

[12] 孫建剛,王向楠,趙長軍.立式儲罐基底隔震的基本理論[J].哈爾濱工業大學學報, 2010,42(4):639-643.

SUN Jian-gang, WANG Xiang-nan, ZHAO Chang-jun. Base theory of seismic isolation of the storage tanks[J].Journal of Harbin Institute of Technology，2010,42(4):639-643.

[13] (GB50761-2012).中華人民共和國國家標準，石油化工鋼制設備抗震設計規范[S].北京：中國計劃出版社.

[14] 崔利富.大型LNG儲罐基礎隔震與晃動控制研究[D]．大連:大連海事大學，2012,6:27-36．

[15] Ayman A S, El-Sharkawy M. Seismic response of base isolated liquid storage ground tanks[J]. Ain Shams Engineering Journal，2011，2:33-42.

Simplified mechanical model for vibration isolation analysis of a vertical storage tank considering swinging effect

SUN Jian-gang1,2, HAO Jin-feng3, LIU Yang3, WANG Zhen1, CUI Li-fu1

(1. College of Civil Engineering, Dalian Nationalities University, Dalian 116600, China;2. College of Civil & Architecture Engineering, Lanzhou University of Technology, Lanzhou 730050, China; 3. College of Civil & Architecture Engineering, Northeast Petroleum University, Daqing 163318, China)

For seismic response analysis of large vertical storage tanks with base isolation, the interaction of soil and structure and the swinging effect of storage tank were considered. Starting from the theory of fluid velocity potential, the boundary conditions of storage tank, storage liquid and tank wall were combined, liquid movement potential function and the corresponding theoretical expressions of base shear, overturning moment and wave height were established. According to the equivalent principle of shear and moment, the simplified mechanical model of a base-isolated tank with swinging effect was established, the motion equation of a vertical storage tank vibration isolation system considering swinging effect was established using the energy principle. At the same time, taking a 15 000 m3large scale storage tank as an example, the vibration isolation effect numerical analysis was performed, and the comparative analysis between the simplified mechanical model of the system and that of the same system without swinging effect was conducted. The results showed that the large scale storage tank with based isolated device can effectively reduce the base shear of the storage tank, it has a poor control effect on liquid sloshing wave height; in a high intensity earthquake area, in the promise of meeting the requirement of sloshing wave height, the upper structure of the storage tank can be designed on the basis of reducing the earthquake intensity.

storage tank; swinging; isolation; seismic response

10.13465/j.cnki.jvs.2016.11.004

國家自然科學基金項目(51478090)；中央財政自主基金(DC201502040403)

2015-03-16修改稿收到日期：2015-05-25

孫建剛 男，博士，教授，1959年4月生

崔利富 男，博士，講師，1982年3月生

TU352.1；TU473.1

A