浙教版八上幾何教學策略
袁丹 孫燕波
摘 要:幾何是初中數學的重要組成部分,而幾何部分的教學又是比較困難的,特別是八年級。其實,在學習幾何時,只要學生掌握好的方法踏踏實實完成,也可以學得輕松有趣。
關鍵詞:幾何教學;基礎知識;應用;歸納總結
幾何難學、難教是一個老話題了。現在我們老師都可以看到這樣兩個現象:一是近幾年寧波中考數學卷上幾何得分率較低,二是新浙教版教材對幾何的要求有所提高。新浙教版教材七年級的幾何學習中以實驗幾何偏多,對演繹推理的要求較低,而八年級上冊第一章是“三角形的初步知識”(其中第三節就是“證明”)、第二章是“特殊三角形”。這樣的安排顯然對八年級學生的幾何學習和教師的幾何教學都是一種挑戰。如何克服這個困難?八上一冊一學期教學下來有以下幾點粗淺的看法:
一、抓好基礎知識很重要
幾何這塊的基礎知識主要包括概念和定理。講清幾何概念和定理,使學生正確理解和靈活運用,這是提高教學質量和培養學生能力的前提條件。
1.關于幾何概念教學的幾點看法
(1)利用教輔工具直觀呈現幾何概念方便學生理解
波利亞說過:“教師的作用在于:系統地給學生發現事物的機會,并給予恰當的幫助,讓學生在情境中親自去發現盡可能多的東西。”學生的認知活動總是從感知開始,由感性認識上升到理性認識。因此利用各種教輔工具直觀呈現幾何概念的形成過程就能使學生容易接受。
例如,八上1.4在講“全等圖形”這個概念時,多呈現一些圖片(有形狀大小完全相同的、有形狀相同大小不同的、有形狀大小都不同的),然后請學生拿兩張疊合試試,就能輕松地發現:形狀大小完全相同的能重合。這時提出“全等圖形”的概念,學生就會感覺直觀、自然,很容易接受這個新知。
(2)通過比較突出概念間的差異加深學生理解
比較,就是將同類事件、人物、現象進行鑒別,找出異同、分清正誤的思維方法,它是提高學生認識事物的重要方法。所以在介紹完新概念后可以舉同類概念的例子要求學生比較差異,這樣有助于加深理解。
例如,八上1.2定義與命題這節中,“命義”“真命題”“假命題”“定理”這幾個概念很容易混淆,特別是“真命題”與“定理”。教學中我讓學生仔細比較發現它們的區別和聯系:定理都是真命題,但真命題不一定都作為定理。
(3)發現概念中的重點字詞使學生的思維更上一層樓
數學概念都簡潔精悍,通過找關鍵字詞及對其的分析能有效提高學生的數學思維。
例如,七年級在講“平行線”概念時,可以請學生分析概念中的重點字詞,如果沒有這些詞會出現什么現象?提示有困難的同學可以找兩支筆代表直線來演示。通過擺弄學生會發現異面直線(當然學生只能感知這樣的線存在卻說不出它的名字),從而知道了“同一平面內”這些字的重要性。這樣不僅開闊了學生的視野,也使學生的數學思維更上一個層次。
2.關于幾何定理教學的幾點看法
定理是解決幾何問題的依據。能根據已知條件和相應的定理正確書寫證明過程的前提是學會對幾何定理的書寫,因為幾何定理的符號語言是證明過程中的基本單位。為了做好幾何定理的教學,我采用“一找、二畫、三寫”三步驟。下面以八上2.3等腰三角形性質定理2:“等腰三角形的頂角平分線、底邊上的中線和高線互相重合“為例說明。
一找:就是要找出命題的條件和結論。有兩個問題:一是只找到“等腰三角形“這一個條件,二是認為“等腰三角形”“其頂角平分線”“其底邊上的中線和高線”都是條件,這樣的認識在實際應用中是有問題的。我認為條件是:“等腰三角形”“三線中的其中之一”,結論是:“另兩條線”,所以嚴格來講這個命題可以分為三個命題來分析。
二畫:在一找的基礎上,畫出相應的圖形。這個步驟中考慮問題要全面、周到。比如等腰三角形你要畫哪類三角形?不同類型的等腰三角形中三線的位置會不會不同?在這里因為鈍角和直角只能作為等腰三角形的頂角,所以底邊上高線的位置只能在三角形內部,所以不會有不同結果,那么只需畫一個類型的等腰三角形
即可。
三寫:有了一找和二畫的基礎,這個過程就相對簡單了。只要將文字語言翻譯成數學語言,將條件放在“∵”后,將結論放在“∴”后。如:∵在△ABC中,AB=AC,AD平分∠BAC,∴BD=DC,AD⊥BC。
二、及時應用新知很必要
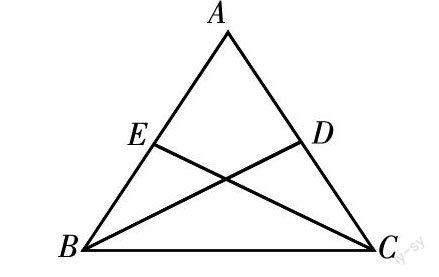
概念、性質的運用是必須的。同時初中生的心理也有好應用、好體驗成功的快樂的特點。所以在概念、性質教學后,通過典型的例題教學是很必要的。八上2.3等腰三角形的兩個底角相等這個性質定理教學后,我安排了這樣一個范例:已知:如圖,在△ABC中,AB=AC,BD、CE是△ABC的角平分線。求證:BD=CE。由于剛接受了新知,學生容易發現∠ABC=∠ACB,又結合角平分線的條件得到∠DBC=∠ECB,從而得到△EBC≌△DBC。這樣一個分析過程對學生來講相對簡單,大多數學生都可以嘗到成功的喜悅,然后在具體書寫時規范一下書寫就可以了。在實際課堂中我并沒有局限于這步,而是從以下幾個方面對這個問題做了挖掘:(1)你有沒有其他的證明方法?(2)你還能發現哪些其他結論?(3)條件中的兩條底角平分線改成腰上的高線或腰上的中線結論還成立嗎?等等。針對這些問題我請學生說說思路就可以了。這樣的安排使學生對幾何性質進行了實際應用,也訓練了學生的幾何思維模式,使學生又一次獲得了成功。最后我也鼓勵全體學生在學習過程中要養成勤思考、多發問的好習慣。
三、做好歸納總結很關鍵
幾何難學的一個主要原因是問題、圖形變化性強,其中的一個條件、圖形甚至只是圖形中的某個點變換一下就可以成為一個新的問題。那么只單單解題是沒有用的,經常做些歸納總結是很關鍵的。課標指出:應該給學生留下足夠的時間內化、整合知識點。關于指導學生歸納總結幾何知識(主要以八上內容為例)我是從以下三個方面入手的:
1.歸納總結常見著眼點
一個幾何問題經常由若干個條件、圖形和結論組成。一個條件或結論往往是解決問題的一個著眼點。以證明相等兩條線段為例,有下列幾種情況:(1)若這兩條線段在同一個三角形中可以考慮等角對等邊來證;(2)若這兩條線段在兩個看似全等的三角形中就可以考慮全等三角形來證;(3)若是上述情況以外的可以考慮通過“第三者”等量代換來證。
2.歸納總結常見特征圖形
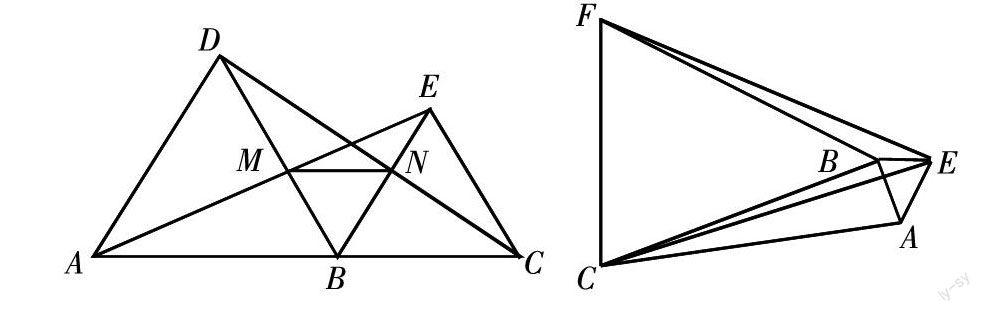
熟悉典型的特征圖形能幫助學生快速解題。比如:(1)如圖:A、B、C三點共線,在AC的同側分別以AB、BC為邊作等邊△ABD與等邊△BCE,AE與BD交于點M,CD交BE于N。可以得到:△ABM≌△DBN、△MBE≌△NBC、△MBN是等邊三角形、MN∥AC等主要結論。在此基礎上遇到下面的問題就會比較容易:以直角△ABC的兩直角邊AB、BC為一邊,分別向外作等邊△ABE和等邊△BCF,連接EF、EC。試說明:(1)EF=EC;(2)EB⊥CF。
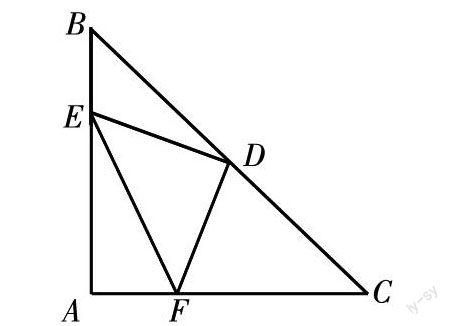
(2)如圖,△ABC是等腰直角三角形,AB=AC,D是斜邊BC的中點,E、F分別是AB、AC邊上的點,且DE⊥DF。通過添加輔助線AD,可以得到:DE=DF;BE 2+CF 2=EF 2;四邊形AEDF的面積總是△ABC面積的二分之一等主要結論。在此基礎上結合后續的函數、四邊形等知識解決一些動態的、綜合性問題就比較容易了。
3.歸納總結常見輔助線
根據條件不能直接解決時要考慮添加輔助線,收集了八上學習中一些輔助線的添法口訣:圖中有角平分線,可向兩邊作垂線;線段垂直平分線,常向兩端把線連;角平分線平行線,等腰三角形來添;要證線段倍與半,延長縮短可試驗。另外在直角三角形中若出現斜邊上的中點可以考慮連斜邊上的中線,在等腰三角形中若出現點邊上的中點可以考慮連底邊上的中線。
綜上所述,學好幾何必須在牢固掌握基礎知識的基礎上,注意平時的點滴積累,多做歸納總結工作。這當然要有一定數量的練習積累,雖然我們不提倡搞題海戰術,但做適量的練習還是必要的,只有量的積累才能帶來質的飛躍。
編輯 范昕欣

