認知系統的邏輯秩序：讓學習真正發生的“道”

【摘 要】理解性學習是讓學習真正發生的基本要素，而數學實驗正是實現理解性學習的一種方式。從數學實驗的視角，構建認知系統的邏輯秩序，是讓學習真正發生的“道”。這里的邏輯秩序包括基礎性的知覺目標、層次性的變異思維、概括性的具身經驗以及科學性的審美關系，它們分別是讓學習真正發生的“頻道”、“通道”、“跑道”和“航道”。

【關鍵詞】初中數學；數學實驗；邏輯秩序；認知系統

【中圖分類號】G633.6 【文獻標志碼】A 【文章編號】1005-6009（2016）33-0023-04

【作者簡介】孫朝仁，江蘇省連云港市教育科學研究所（江蘇連云港，222006）所長，正高級教師，江蘇省特級教師，初中數學實驗手冊副主編。

“讓學習真正發生”，這是第11屆江蘇省“杏壇杯”蘇派青年教師課堂教學展評活動的主題。筆者有幸聆聽了幾位蘇派青年教師的課堂教學，在領略了蘇派青年教師教學風采的同時，也一直在揣摩這一主題的真實內涵。我們知道，學生是教學過程中的主體，“教學從學生出發”是課堂教學最重要的特征之一。但是，受學科特點的影響及呈現形式等因素的制約，教材通常是以靜態的方式直接呈現知識結論，這些結論對于成人來講是很容易理解的，但對學生來講，卻不容易理解。毋庸置疑，不理解性的學習，就不可能深入學科的本質，也不可能觸及學生的心靈，更不可能促進學生對于知識的持續建構，這樣的學習一定不會真正發生。因此，筆者認為，理解性學習是讓學習真正發生的前提。

從數學學科來說，由于其“高度的抽象性、嚴密的邏輯性以及廣泛的應用性”而顯得學習“枯燥無味”，學生的學習便不會真正意義上得以發生。基于此，在傳統的數學課堂教學中，引進數學實驗這一學習方式可以助推學習的真正發生。數學實驗是學生通過動手動腦，以“做”為支架的數學教與學的活動方式，是在教師的引導下，學生運用有關工具，通過實際操作，在認知與非認知因素參與下進行的一種發現數學結論、理解數學知識、驗證數學結論的思維活動。可以說，數學實驗充分突出了“智者明‘法，慧者通‘道”的學習秩序與法理，是數學理解性學習的基本方式。“明法”就是合目的性、合規則性、合法理性；“通道”就是學習范式符合“道”的要義（一生二、二生三、三生萬物）。換言之，數學實驗是打通讓學習真正發生的“道”。這里的“道”就是構建認知形態系統的邏輯秩序，關乎知覺認知目標的確立，關乎變異認知思維的激發，關乎具身認知經驗的積累，更關乎審美認知關系的梳理。

一、知覺目標：認知形態系統的基礎性邏輯秩序，找準讓學習真正發生的“頻道”

知覺是解釋外界客體和事件產生的感覺信息的加工過程，是對現實的感性反映，具有整體性、恒常性、意義性和選擇性特征。目標是課程的精神統領和行動指南，是教學設計與實施的思維線索。“經歷”“體驗”“探索”是對“做數學”行為目標的生動刻畫，與知覺目標具有內部關系的一致性，反映初中段學生的感性思維好于理性思維的“思維事實”。數學實驗突出“做”“視”“說”“用”的知覺特征，用“感知”“感受”“感悟”“領悟”等感官類動詞刻畫知覺目標。

梅洛·龐蒂從知覺現象學出發，認定身體是認識世界的通道，身體知覺具有認識世界的能力，是人認識世界的基點。[1]數學實驗的本質就是通過身體“做”數學的行為獲得對新概念、新原理和新方法的領悟與理解，因此，這樣可以很好地找準讓學習真正發生的“頻道”。在“做”數學實驗范疇，知覺目標涵蓋“四個頻道”：一是通過“觀察”，感知概念的局部屬性；二是通過“知覺選擇”，感受概念的本質屬性；三是通過“建立表象”，感悟概念的整體屬性；四是通過“意義表征”，領悟概念間的內部關系。在課堂教學中，如果調適好這“四個頻道”，不僅可以體現數學實驗在數學教學中的補注作用，而且也可以發揮提升學生學力的功能，更可以構建知覺在學理意義上的邏輯秩序，“四個頻道”協調運作，學習自然會真正發生。

以“認識簡單幾何體”主題活動為例：首先，讓學生觀察長方體，借此認識棱柱和棱錐，并根據圖形特征進行分類；其次，讓學生折疊棱柱和棱錐，并進行觀察和描述；最后，以小組合作的形式進行集體活動，摸出指定的幾何體并分工描述其特征。為此，確立的知覺目標是：學生通過對實物圖片的欣賞和生活中物體的觀察，抽象感知幾何圖形，會用數學的眼光觀察世界；學生經歷對幾何圖形的分類過程，感受立體圖形和平面圖形之間的區別，對幾何圖形的抽象有進一步的認識，會用數學的思維分析世界；學生經歷折紙和摸幾何體的數學實驗，感悟立體圖形和平面圖形之間的內部關系，并通過小組合作，描述幾何體的活動，領悟用幾何語言表達世界的意義。

就主題活動的邏輯秩序來說，“觀察”“欣賞”幾何體行為是知覺認知目標的邏輯起點，“折疊”“描述”幾何體行為是知覺認知目標的邏輯過程，“摸出”“表征”指定幾何體行為是知覺目標的結果狀態，反映認知形態系統的邏輯理序。就數學學習論來說，觀察是知覺認知的邏輯基礎，操作是知覺加工的邏輯手段，表征是知覺學習的邏輯通道，有了這些，學生對于“認識簡單幾何體”的學習才有了真正發生的基礎。本次展評活動中，有一節“正方形中的45°美”的課，執教者通過“在正方形中旋轉三角板”創設認知情境，找準了認知的邏輯起點，繼而讓學生自主尋找要探究的問題，完善了認知過程，最后讓學生“學以致用”，反映了知覺目標的結果狀態，“三位一體”奏出了“讓學習真正發生”的和諧音符。

二、變異思維：認知形態系統的層次性邏輯秩序，構筑讓學習真正發生的“通道”

變異思維作為數學命題認知的一種思維方式，得到馬頓（Marton）變異理論的強有力支撐。[2]該理論的核心思想是“學習源于變異”，也就是說，變異（Variation）、審辨（Discernment）和同時性（Simultaniety）是讓學習真正發生的基礎要素，變異思維是學習的基本通道。而數學實驗正是在突出概念變異、原理變異以及經驗變異的審辨與同時性特征的基礎上，形成概念法則的邏輯連貫性認識體系，進而促進心理概念圖的建立和認知形態系統邏輯秩序的規范形成。

米山國藏的《數學的精神、思想和方法》一書從變異思維的邏輯出發，認定數學是由簡單明了的事實與邏輯推理結合一步一步構成的。[3]這里的“一步一步”就是對變異思維的具體刻畫，前“一步”思維是后“一步”思維的基礎，后“一步”思維是前“一步”思維的變異，正因為如此，學生的學習在這“一步一步”的過程中得以真正的發生，實現學生接受“更好的教育”的質量目標也才能實現。[4]因此，我們規約操作范式邏輯秩序為：一是變異情境維度，突出概念審辨思維的立體遷移；二是變異問題發問方向，突出原理加工程序的概括性特征；三是變異經驗現有發展區（由單稱現有經驗發展區到復稱事實經驗水平區），突出新舊經驗的同時性重組與同時性改造的特征，以此構筑變異思維初始目標良性遷移的通道。

例如：在探索“基本圖形性質”這一主題時，通過“折紙與證明”這一數學實驗，突出變異思維特征，完成對“合情推理”認識的變遷，最終把握基本圖形內部關系。具體活動安排如下。首先，實驗目標是經歷折紙過程，感受證明的必要性以及合情與演繹的內部關系，進一步發展合乎邏輯的思考秩序和有條理的表達能力。其次，讓學生在折紙活動中，體驗目標的適配性和可接近性。從三個維度進行思維聚焦：一是讓學生用長方形紙片折出一個正方形，說明理由并進行可行的驗證；二是讓學生用長方形紙片折出一個菱形，并在說理的基礎上驗證結論的合理性；三是讓學生用正方性紙片和長方形紙片各折出一個等邊三角形，并在推演的基礎上驗證結論的可靠性。最后是讓學生設計盡可能多的“‘做菱形”的方案，并探究如何用足夠長的紙條折出一個正五邊形。

目標是思維的依據，變異目標的確立為實驗活動的邏輯展開提供了思維秩序，構筑了思維通道。如果說“折正方形→折菱形→折等邊三角形”思維變化過程是情境變異思維秩序的集中表現，那么“變異目標的建立→變異問題反應塊的組織→后實驗方案的編制”的思維秩序，是程序性加工概念圖得以建立的具體表現，而探究折正五邊形的思維流變行為是變異經驗發展區的內部秩序，反映了認知系統的層次性邏輯秩序，體現了程序性加工審辨的科學性以及信息流的適配性。本次展評活動中來自南京市蓮花實驗學校初中部的金明明老師執教的“平面圖形的密鋪”一課，就是讓學生經歷“選擇一種形狀、大小完全相同的正多邊形進行密鋪”到“從邊長相等的正三角形、正四邊形、正六邊形和正八邊形中選擇兩種合適的正多邊形進行密鋪”再到“用形狀、大小完全相同的任意三角形、任意四邊形進行密鋪”這樣“一步一步”的“變異”過程，既動手又動腦，真正學習自然發生。

三、具身經驗：認知形態系統的概括性邏輯秩序，規劃讓學習真正發生的“跑道”

具身認知（Embodied Cognition）主張“認知是通過身體的體驗及其行為活動方式而形成”。[5]這就強調人的身體在認知過程中起到了不可替代的作用。已有研究表明：身體的物理屬性對認知的內容具有直接的作用，這種作用不僅體現在現實物質概念上，同樣體現在抽象的理性概念上。[6]當然，這些抽象概念的獲得與保持不完全依賴于身體的具身經驗（感覺經驗），這也是數學活動經驗需要在“做”的過程和“思考”的過程中逐步積累的邏輯根據。這里的“做”突出“現實物質概念”的本體特征，而“思考”側重突出“理性概念”特征，從而形成具身經驗產生式系統（做數學→理解數學→具身經驗）。

在經典學習心理學理論中，大腦的學習方式主要可以分為兩種：聯想學習（associative learning）和觀察學習（observational learning）。[7]把“神經學”借用到數學實驗范疇，則可以把“觀察學習”看作是“做”數學的邏輯手段，“聯想學習”看作是“用”數學的邏輯思維，這也是讓學習真正發生的兩條“跑道”，缺一不可，需要我們科學地規劃。這些經驗性和擬經驗性的邏輯秩序，內在地支配著認知形態系統的概括性能力。當然，觀察學習始于現實經驗，終于重組經驗，對行為模仿、社會技能習得、文化傳播以及價值觀形成起到關鍵作用。聯想學習始于定向經驗，終于素養經驗，對記憶、情緒、習慣以及獎懲系統的形成至關重要。因此，數學實驗在具身經驗層面的邏輯秩序可從三個維度進行規劃：一是讓學生在相似情境經驗中，進行同化性具身實驗；二是讓學生在半開放問題解決中，進行順應性具身實驗；三是讓學生在“中間變量”（機體的內部變化）的行為中，進行重組性具身實驗，形成具身經驗可靠性范式。

例如，在進行“估算”這一概念教學時，設計了易于實踐的“折紙”活動，集中反映具身經驗獲得的邏輯秩序。具體流程概括如下：首先，讓學生取出一張標準報紙，嘗試對折8次，猜想、驗證疊后報紙的厚度，并算出一張報紙的可能厚度；其次，讓學生解決一張報紙連續對折30次后，其厚度的估計值，并與珠穆朗瑪峰的海拔高度相比較；再次，讓學生估計《數學實驗手冊》的厚度，并說明個體結論獲得的過程；最后，讓學生設計編制估算蘇科版七年級《數學》上冊教科書厚度的預案，以及如何估測該書100頁、50頁、10頁和1頁的厚度。另外，讓學生逆向估計多少本這樣的教科書壘成的高度才能為1米，并用1米高的課桌驗證結論的接近度。

僅從具身認知邏輯秩序來說，“折→疊→猜測→估算→驗證→比較”等具身認知行為，是同化概念經驗的具體表現；“編制→估計→度量→推算”一本書的厚度、部分書頁的厚度，是順應概念經驗的逆向思維表現；“估測報紙的厚度→估測手冊的厚度→估測教科書的厚度”以及由“執行方案”到“制定、實施方案”是“中間變量”重組建立新經驗體系的過程，反映具身經驗在問題解決與提出中的改造作用。經歷這樣的反復認知與實踐過程，在“觀察”與“聯想”這兩條“跑道”上行進，學生對“估算”這一概念的學習自然是真正的發生。本次展評活動中的“函數”一課，執教者通過創設動態的“汽車加油”情境，讓學生有“身臨其境”的具身感，后續學習的通道自然打開。

四、審美關系：認知形態系統的科學性邏輯秩序，開通讓學習真正發生的“航道”

審美是數學學習的開端，“哪里有數，哪里就有美。”（普洛克拉斯語）審美關系是直覺思維的表現形式，帶有強烈的“天地與我共生，萬物與我為一”的整體性特征。這就好比孩子認母親，都是從“整體”來觀察，可以說這種審美的整體性就是讓學習（認知）真正發生的“航道”。數學實驗是直覺思維的重要載體，能讓學生在科學方法的選擇中不斷地發展審美邏輯秩序。數學實驗的整體性表現在審美選擇關系層面、審美建構關系層面以及審美邏輯關系層面，認證活動對象的整體屬性本身就是審美關系科學建構的結果狀態。龐加萊“從直覺是一種無意識思維活動的觀點出發”，證實“在無意識的活動中，審美情感發揮著選擇作用”，從而認定選擇的直覺經常表現為美的直覺。[8]實踐表明：讓學習真正發生的“好課堂”“好念頭”抑或是“好問題”往往帶有數學審美特征。數學實驗作為“好課堂”重視心理審美環境的建設，“數學實驗室”的建立就是對環境審美的外化，“課題學習”就是好念頭或好問題做出選擇的心理范式，從這一意義層面來說，數學實驗也是建立審美關系的“航道”，反映認知形態系統的科學性邏輯。

許多數學家從數學是藝術出發，認定一個科學理論成就的大小，事實上就是它的美學價值的大小；科學結論的合理性要在它的審美價值中去尋找，并用它來判定科學方法的合理性。[9]在數學實驗審美關系范疇，可以從以下三條“航道”直達美的直覺：一是變化問題情境，突出思維的相似性特征；二是變換問題角度，突出思維可辨性特征；三是變化監控方式，突出思維的獨立性特征。

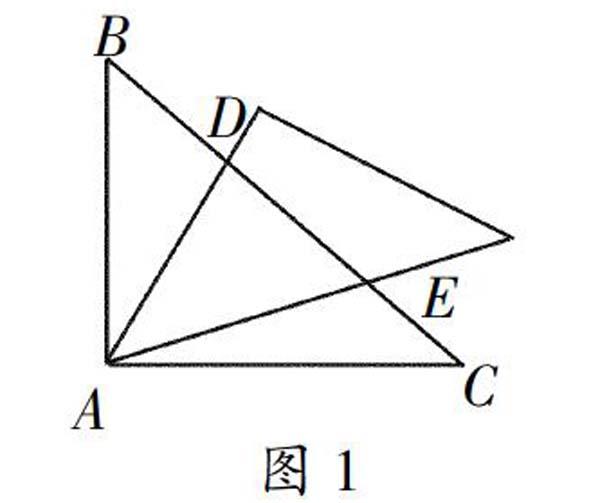
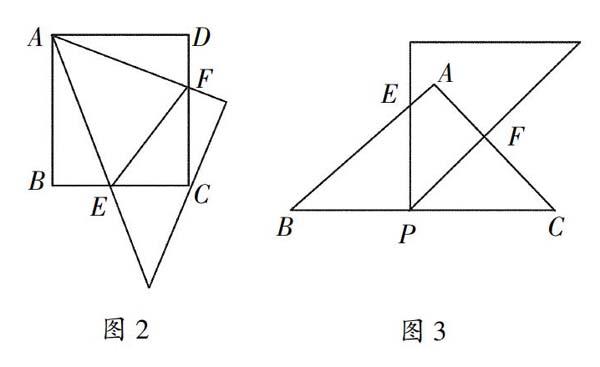
例如，為揭示“旋轉不變”的邏輯屬性，基于審美關系我們設置了“玩三角板”的數學實驗，其基本流程如下——首先，讓學生剪出一對全等的直角三角形紙板，并取其中一張沿直角頂點，經過兩次折疊，折出一個45°角。其次，讓學生（兩人合作）將全等的等腰直角三角板按圖1的方式放置，寫出其中非全等的相似三角形以及線段BD、DE、CE之間的數量關系并說明理由。第三，讓學生按圖2方式疊放正方形紙板和等腰直角三角形紙板，猜想線段BE、DF、EF之間的數量關系并說明理由；連接圖2中的線段BD交AE于點M，交AF于點N，直接寫出BM、MN、ND之間的關系。最后，讓學生按圖3的方式疊放全等的等腰直角三角板，并繞點P旋轉，寫出旋轉過程中所有非全等的相似三角形，并說明理由以及寫出可能存在的函數關系。

審美是自由的表征，是自由創造的途徑和中介，是持續性學習（真正發生的學習一定是持續性學習）的潤滑劑。“剪出→折出→疊放→旋轉”行為動作是審美關系得以建立的直覺基礎，突出情境相似性特征，反映認識形態系統的科學統一性；“單稱相似變換→復稱全等變換→復稱相似變換”的直覺思維運動行為是審美關系建立的邏輯基礎，突出“變換角度看問題”的審美意義，反映認識形態系統的可辨性特征；“不穩態二次數量關系→穩態一次數量關系→穩態二次數量關系→穩態函數關系”的審美行為是審美關系得以提升的邏輯秩序，帶有強烈的獨立性特征，反映數學實驗在科學與審美范疇的共通性價值秩序。前文所提到的“正方形中的45°美”一課，其審美關系的建立也是可圈可點的，讓學習真正發生的“航道”非常暢通。

綜上，認知系統的邏輯秩序，存在于每一個具體行為的背后，揭示讓學習真正發生的“道”。其中，知覺目標的確立是其邏輯根據，變異思維和具身經驗是邏輯基礎，審美關系是邏輯線索，四者共同作用，可使得學習真正發生。

【參考文獻】

[1]楊曉.知覺教學：身體現象學對教學改革的啟示[J].課程·教材·教法，2015（12）.

[2]王光明.數學教育研究方法與論文寫作[M].北京：北京師范大學出版社，2010：44.

[3]米山國藏.數學的精神、思想和方法[M].毛正中，吳素華，譯.成都：四川教育出版社，1986：56.

[4]楊孝如.“更好的教育”：基礎教育發展的時代命題——專訪江蘇省委組織部副部長、中國教育學會副會長胡金波[J].江蘇教育研究，2015（9A）.

[5]葉浩生.具身認知：認知心理學的新取向[J].心理科學進展，2010（05）.

[6]殷明，劉電芝.身心融合學習：具身認知及其教育意蘊[J].課程·教材·教法，2015（07）.

[7]陳巍，汪寅.基于鏡像神經元的教育：新“神經神話”的誕生？[J].教育研究，2015（02）.

[8]蕭柏榮.數學教育探索五十年[M].南京：南京大學出版社，2012：50.

[9]王欽敏.感受數學美的兩個重要途徑[J].數學教育學報，2014（02）.