發(fā)動機軸承故障診斷方法的研究

許同樂，高朋飛，陳 康，侯蒙蒙

（山東理工大學 機械工程學院，山東 淄博 255049）

發(fā)動機軸承故障診斷方法的研究

許同樂，高朋飛，陳 康，侯蒙蒙

（山東理工大學 機械工程學院，山東 淄博 255049）

針對EMD（Empirical Mode Decomposition）方法中存在的端點效應和IMF（Intrinsic Mode Function）虛假分量過多的問題，提出了基于互相關的EMD方法。首先，對非平穩(wěn)性信號進行互相關延拓消除端點效應；其次，對消除端點效應的信號進行EMD分解，并將分解后的IMF與原信號作互相關，保留與原信號最相關的IMF；最后，作出信號的Hilbert邊際譜，識別信號的頻域特征。仿真結果表明該方法能夠有效地克服端點效應，分離出真實IMF。將其應用于船舶發(fā)動機滾動軸承故障診斷中，能有效地識別出故障特征。

EMD分解；端點效應；相關選擇法；故障診斷；IMF

0 引 言

感應電動機在船舶中應用得非常廣泛。一旦電機發(fā)生故障，就可能威脅船舶航行的安全。軸承是電機的重要部件，其故障率在電機故障中是最高的，為了發(fā)現電機軸承早期的故障，本文應用EMD方法研究電機軸承的振動信號，以減少船舶在航海中出現危險。但是EMD存在端點效應、IMF個數過多等問題。端點效應會使分解的IMF數據兩端產生振蕩現象。這會引起兩個問題，一是對IMF的影響會逐漸向內“污染”整個數據序列而造成分解結果嚴重失真；二是對IMF進行Hilbert變換時，信號兩端也會產生發(fā)散現象，得到的Hilbert譜將不能反映信號的特征[1-3]。因此，船舶發(fā)動故障診斷領域中，應用EMD方法處理故障信號，須克服端點效應，才能進行準確的Hilbert分析。

1 EMD分解原理

EMD方法可以將任何一個復雜信號分解成若干個IMF之和，它基于兩個基本假設：任何一個復雜的信號都是由若干個不同的IMF組成的，每一個IMF都具有相同數量的極值點和過零點，在相鄰的兩個過零點之間只有一個極值點，而且上下包絡線關于時間軸局部對稱；任何一個信號都可以包含有若干個IMF[4-7]。在此假設基礎上，EMD方法可以對任何信號進行分解。其分解步驟為：

這樣，信號x（t）分解成了若干個IMF和殘余量之和的形式，如下式

不同的IMF反映了信號中不同的頻率成分，先分解出的IMF分量為高頻分量，后分解出的IMF分量為低頻分量，直至殘余項變?yōu)閱握{的趨勢項。因此，EMD方法完全由信號本身決定，是一種自適應的信號分解方法。

2 端點效應及解決方法

由EMD分解原理可知，必須確定出信號所有的極值點，才能作出信號的包絡線，獲得準確的IMF。當信號端點不是極值點時，在包絡線的擬合過程中會出現誤差，表現為得到的IMF數據兩端產生振蕩現象。這種由端點不是極值點而造成的端點振蕩稱為端點效應。

目前，很多學者對于端點效應問題采取的大都是數據延拓的方法，如胡勁松等[8]應用AR模型預測端點極值進行延拓，證明了其有效性，并將其應用于轉子橫向裂紋的時頻分析，取得了較好的效果；曹端超等[9]對鏡像延拓法、平行延拓法、極值延拓法和多項式擬合延拓法4種抑制端點效應方法進行了比較，提出了端點效應評價指標，最終得出鏡像延拓法效果最好，仿真分析與實際分析都對此做了證明。但是對于數據延拓這種方法，本身存在有一種內在的誤差，對于不同的信號，其延拓精度也會有很大的差別，因此，其應用存在一定的局限性。為此，本文提出一種新的抑制端點效應的方法。

由于軸承屬于旋轉機械設備，其振動信號必有一定的周期性。也就是說，排除誤差干擾，端點處的數據必然在若干個周期后再次出現，因此，可以通過尋找與端點處數據最相近的波形進行延拓，具體步驟如下（以左端點為例）：

（2）從tp3時刻開始，選取長度為L的波形，記為A2；以此類推，依次向右移動1個數據點，選取長度為L的波形，分別記為A3,A4,…。

（3）將A1與A2,A3,A4,…分別進行互相關計算，公式如下：

式中：n為信號長度，x，y為各個采樣點上的信號值。

按同樣的步驟進行右端波形的延拓，這樣就獲得了延拓后完整的波形。然后對此信號進行EMD分解，在將延拓后的部分去掉，就能得到比較準確的結果，有效地克服了端點效應。該方法很好地考慮了信號內部的變化，使信號延拓后能光滑地過渡，而且對于內部的奇異數據點也能很好地處理，具有較強的自適應性。

3 IMF的選擇方法

端點效應產生的誤差會向內傳遞給整個數據，這樣就會產生一些虛假的本征模分量，對于分解出來的低頻成分來看，問題尤其嚴重。當數據比較復雜，噪聲比較大時也會出現這一問題。如果不將它們剔除，無疑將誤導人們對信號的分析。因此，有必要將這些虛假分量找出，并將它們剔除。

由于本征模分量是由原始信號分解得到，是對原信號的一種近似正交的表達，因此那些真實的本征模分量與原信號之間有很好的相關性，而那些由端點效應和噪聲得到的虛假的本征模分量和原信號之間的相關性則很差，因此本文提出了一種相關選擇法。將EMD分解后的本征模分量和原信號的相關系數作為一個指標，來判斷哪些是真實的本征模分量，哪些是虛假的、無意義的本征模分量，并將虛假的本征模分量累加至殘差部分。

為了避免把一些幅值較小的真實的本征模分量剔除，將原信號與IMF作歸一化處理。這樣，所得到的最大相關系數為1。假設得到所有的相關系數為μi，作以下處理：

4 仿真實驗與實際診斷實例

4.1 仿真實驗

為驗證改進方法的分解效果，論文進行了模擬仿真。構造信號x如下：

采樣點數為512，選取信號的范圍在1～2 s區(qū)間內，原始信號如圖1所示。

由公式（7）可知，原信號中包含有兩種頻率成分，還有部分噪聲。但是圖2分解結果卻有6個IMF,而且IMF兩端都有振蕩現象。這說明分解過程中發(fā)生了端點效應，使分解的IMF數據兩端振蕩，而且由于內部數據受到端點效應的影響，進而產生了一些虛假的IMF，而使IMF個數過多。對IMF做Hilbert邊際譜，結果如圖3所示，由圖中可以看出，振蕩現象以及過多的IMF影響了Hilbert分析的準確性，圖中低頻處較混亂，不易辨別信號的真實頻率。

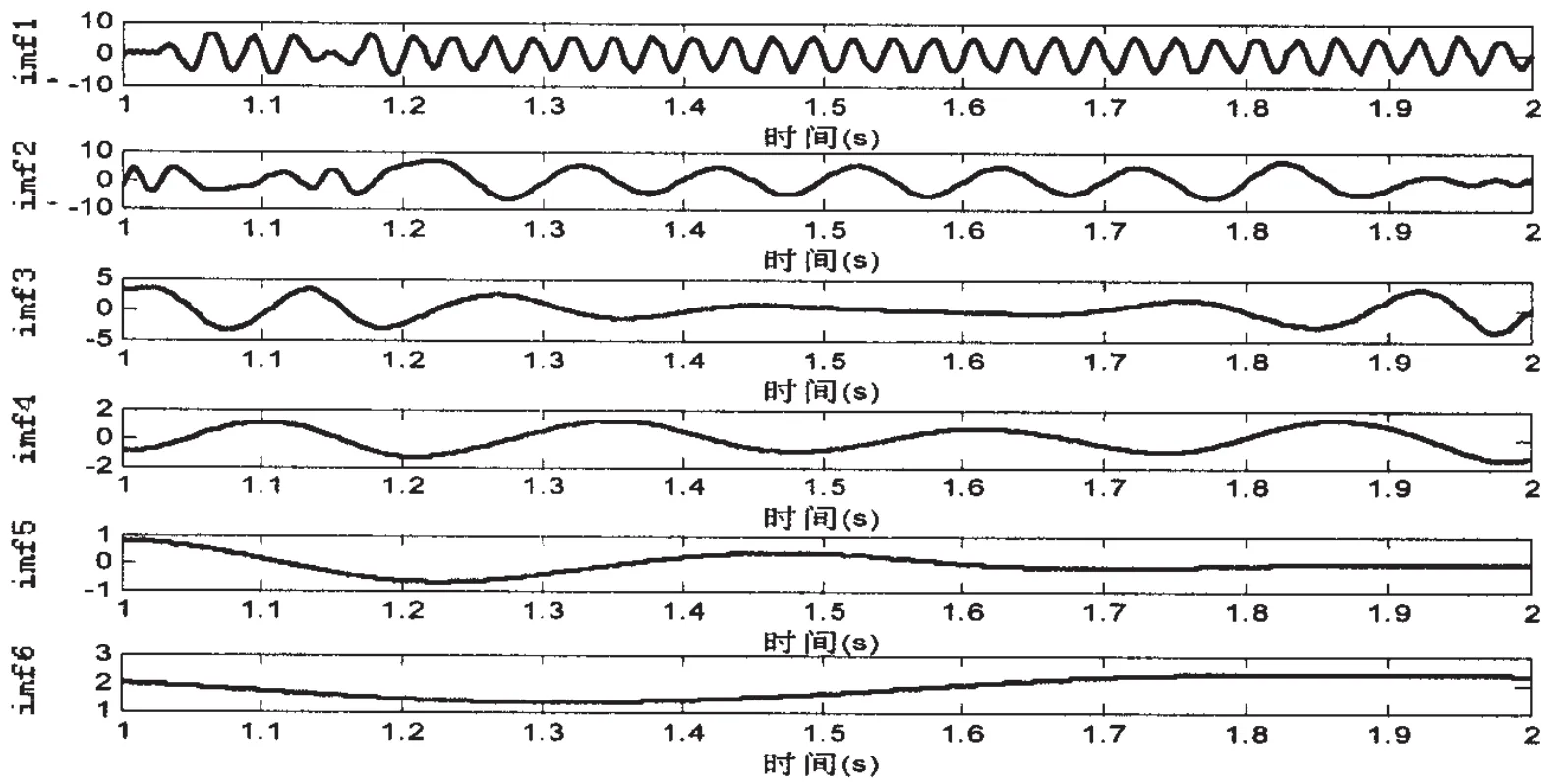
圖2 直接EMD分解結果Fig.2 The decomposition result by direct EMD

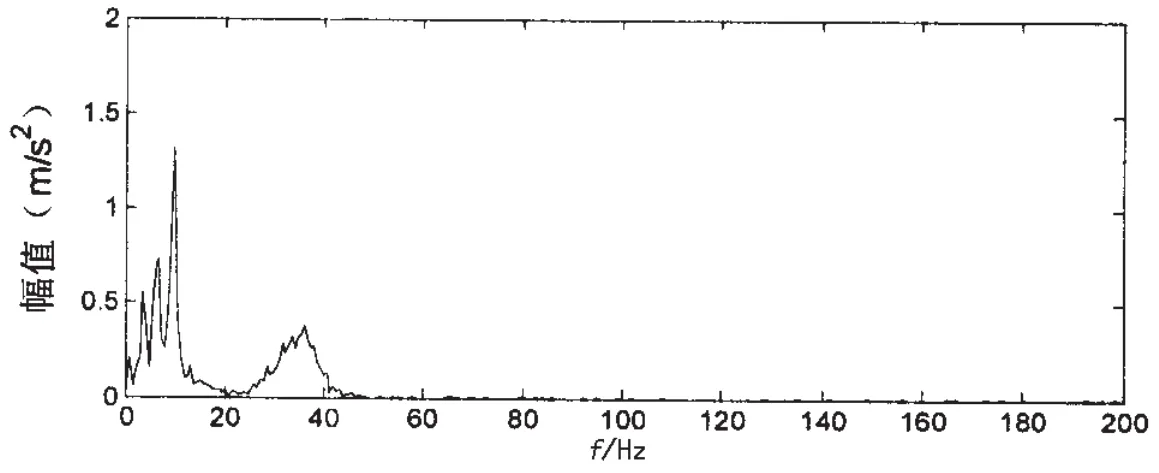
圖3 直接EMD分解結果的Hilbert邊際譜Fig.3 The Hilbert marginal spectrum of direct EMD decomposition results

表1 IMF與x相關系數表Tab.1 Tables of the IMF and original signal x correlation coefficient

為便于比較，使用消除端點效應方法對信號做EMD分解，分解結果如圖4所示。

由圖4可以看出，EMD的端點效應得到了有效的解決，IMF數據兩端的振蕩現象消失，但是分解結果多了一個頻率分量，這是由于EMD分解的自適應性決定的。圖中可以看出該分量幅值很小，屬于噪聲成分，應當予以剔除。

使用相關選擇法對消除端點效應的信號進行EMD分解，相關系數如表1所示。將相關系數小于閾值的分量剔除，疊加到殘差里面。分解結果如圖5所示。

由圖5可以看出，該方法克服了端點效應和IMF虛假分量過多的問題，已經基本實現了原始信號的頻率分離，而且誤差error恰好是信號中的殘余分量。對分解結果進行Hilbert分析，如圖6所示，由圖中可以看出，Hilbert邊際譜很完美地將信號頻率成分分離開來，經過計算，兩條頻率成分恰好為原始信號的兩個頻率分量，仿真效果很好。

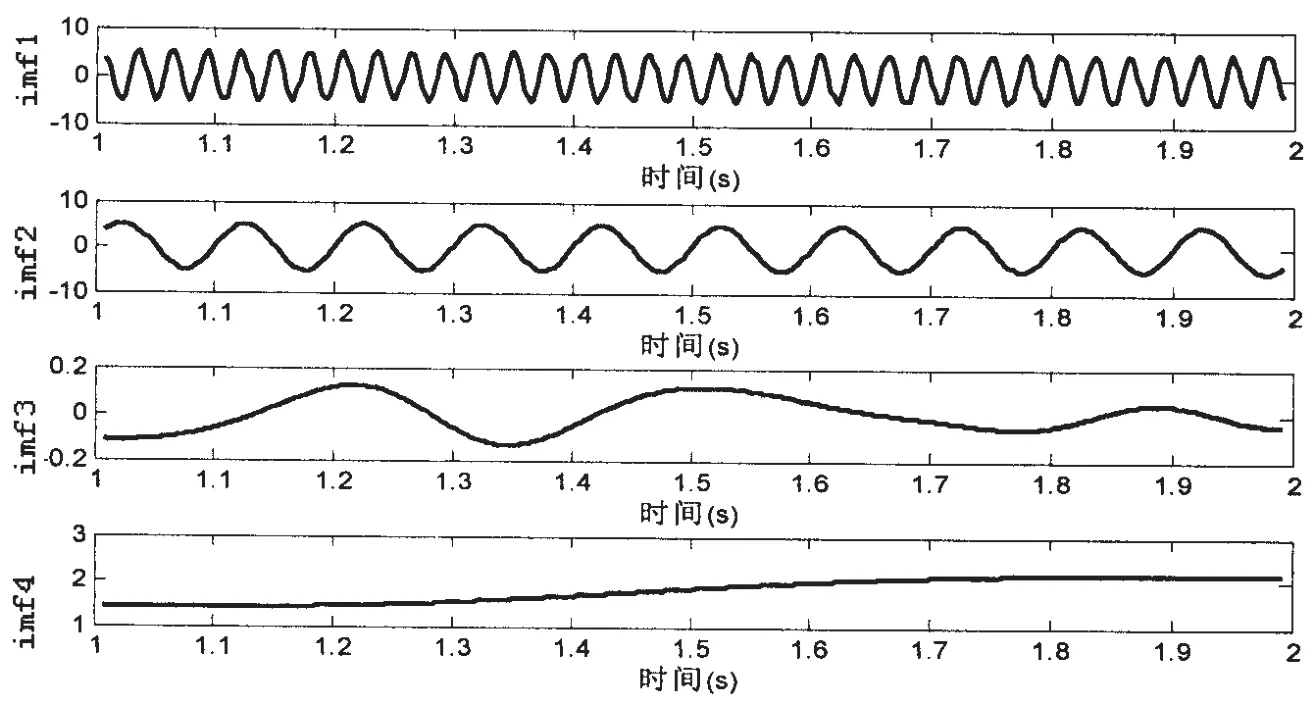
圖4 消除端點效應后的EMD分解結果Fig.4 The EMD decomposition result after eliminate end effect

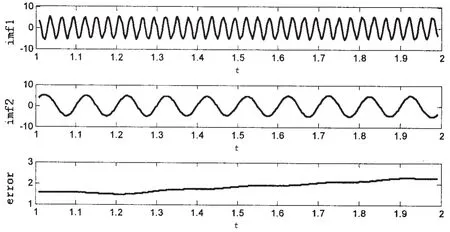
圖5 相關選擇后的EMD分解結果Fig.5 The EMD decomposition result after correlative selection

圖6 相關選擇后EMD分解的Hilbert邊際譜Fig.6 The EMD decomposition results of Hilbert marginal spectrum after correlative selection

4.2 實際診斷實例

本文根據該方法對輪船發(fā)動機軸承進行故障診斷，如圖7為滾動軸承外圈故障振動信號，轉速為855 rpm，采樣頻率為6 000 Hz。經EMD分解如圖8所示，由圖中可以看出信號被分解為11個從高頻到低頻排列的本征模函數，而且端點存在著明顯的振蕩現象。這是因為原信號本身是一種復雜的信號，包含有各種頻率幅值的有用信號，還有周圍環(huán)境的噪聲影響，信號的復雜性決定了EMD必然會分解出一些虛假分量；而且由于端點不是極值點使得端點效應問題凸顯。這些問題顯然不利于對信號的進一步分析，由圖9信號的Hilbert邊際譜可以看出頻率分量較多，而且故障頻率不明顯，無法做出診斷。

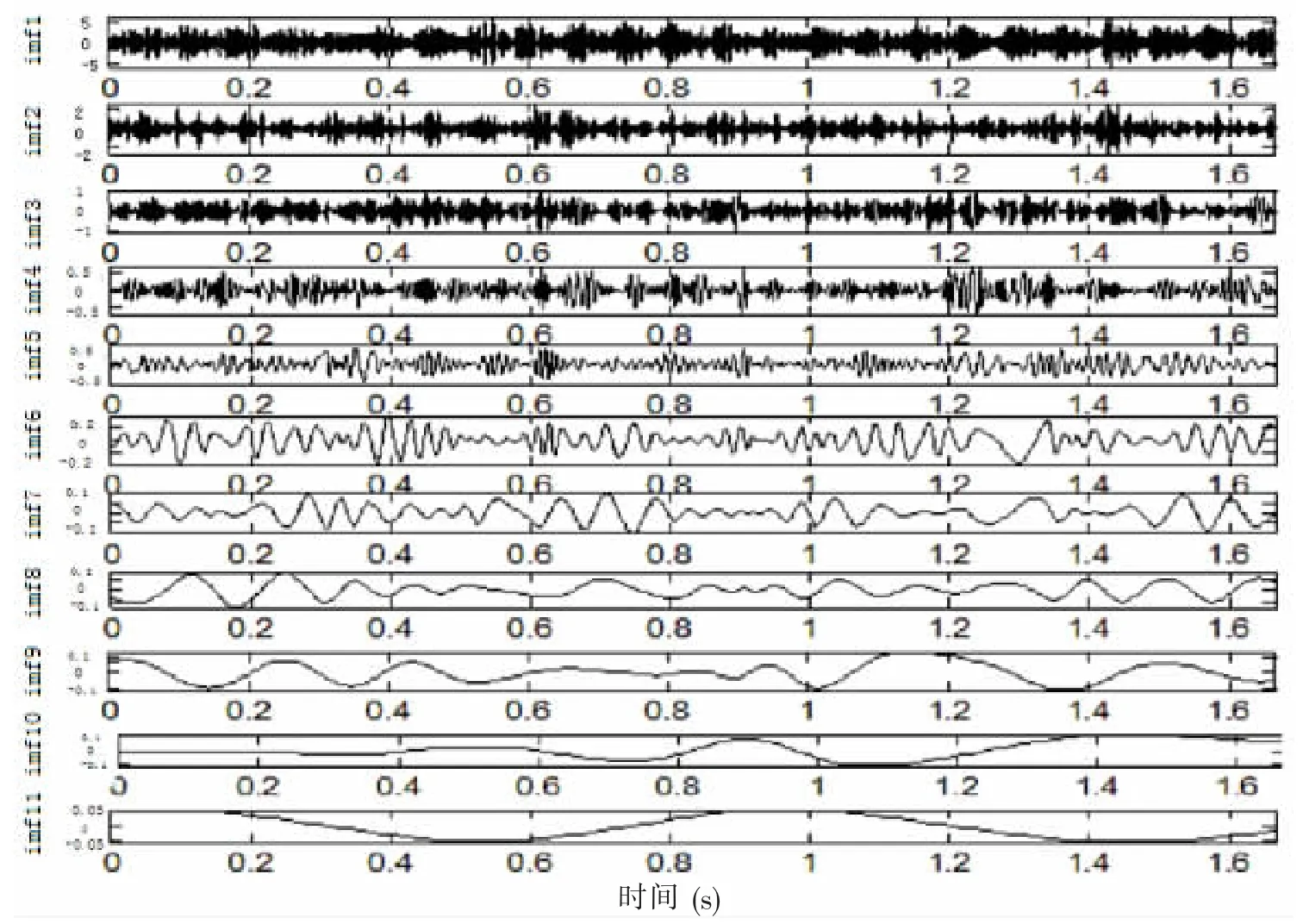
圖8 EMD分解IMf1-IMF11Fig.8 The EMD decomposition results of IMf1-IMF11

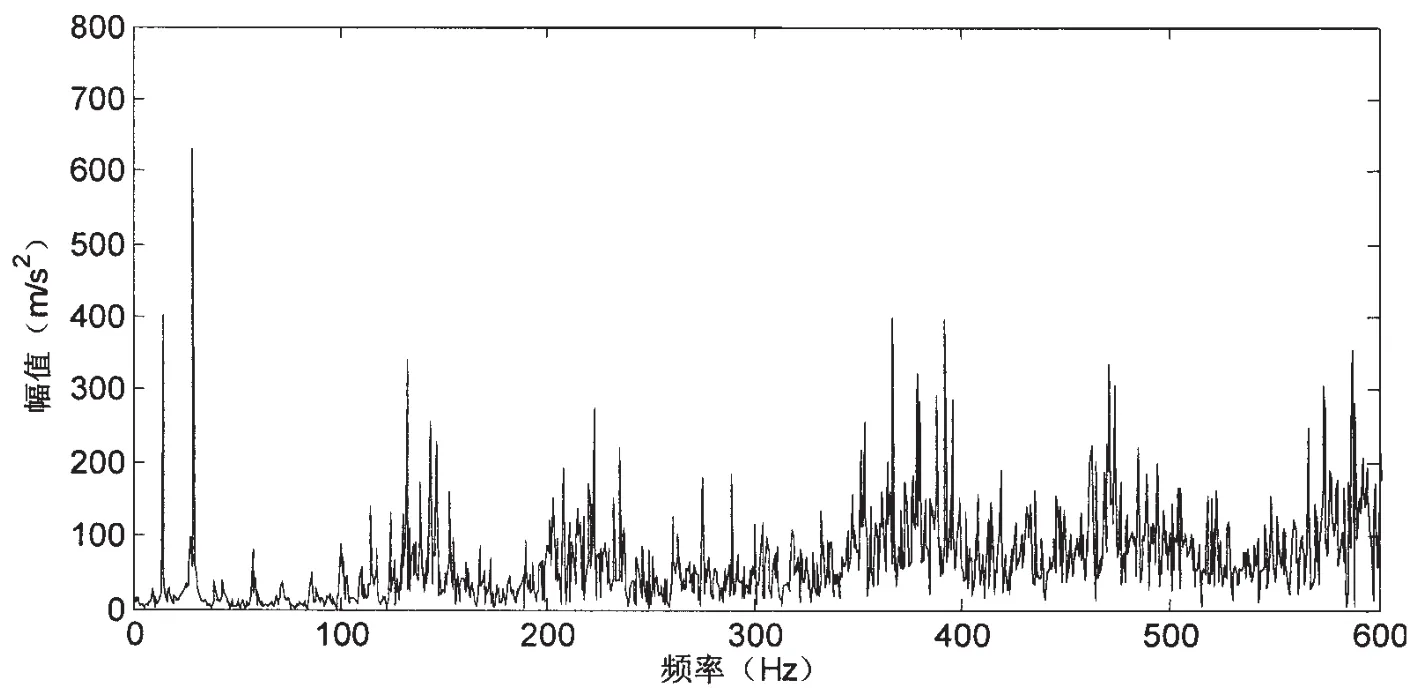
圖9 EMD分解信號的Hilbert邊際譜Fig.9 The Hilbert marginal spectrum of EMD decomposition results

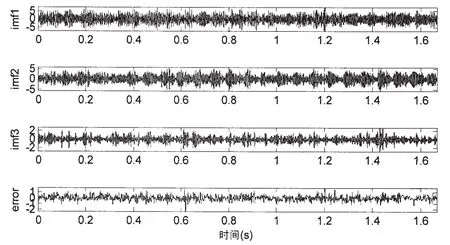
圖10 本文方法EMD分解結果Fig.10 The decomposition results by the presented method in this paper

圖11 本文方法EMD分解的Hilbert邊際譜Fig.11 The Hilbert marginal spectrum by the presented method in this paper

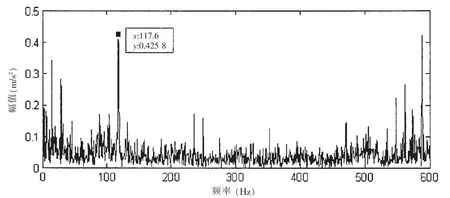
圖12 本文方法Hilbert包絡譜Fig.12 The Hilbert envelope spectrum by the presented method in this paper

使用基于相關分析的EMD方法進行分解，可以克服端點效應和虛假分量過多的問題。分解結果如圖10所示，由圖中可以看出，結果中有3個本征模函數分量以及一個error分量，很好地解決了虛假分量過多的問題，而且對端點效應的抑制也取得了很好的效果。

從時域圖中不容易看出一些特征信息，作出其Hilbert邊際譜，如圖11，從中可以清晰地辨認出14 Hz、28 Hz、117 Hz、235 Hz、352 Hz、471 Hz、587 Hz等頻率分量。14 Hz是轉軸的轉頻，在28 Hz幅值較大說明轉軸或軸承存在不對中現象。而117、235、352、471、587 Hz是軸承外圈故障頻率的基頻和諧頻，可以推斷出軸承外圈存在故障。圖12是信號的Hilbert包絡譜，在基頻117 Hz和其諧頻處也存在較大幅值，可以確定為軸承外圈發(fā)生故障。

通過采用互相關分析的EMD方法進行分解，可以最大程度地分解出信號的特征信息，而且便于進一步分析，正確地識別信號的頻率成分，從而可以進行故障的診斷。

5 結 語

在對船舶電動機軸承故障信號分析過程中，如果對信號直接進行EMD分解，會產生端點效應問題以及過多的虛假分量，這會對診斷結果產生不利影響。為此本文提出了基于波形互相關分析的EMD方法，波形互相關延拓很好地克服了端點效應，IMF的相關選擇方法則剔除了過多的虛假分量。將該方法應用到船舶電動機軸承故障分析中，結果表明改進的方法能夠有效地克服端點效應現象，多余的虛假分量被剔除；診斷結果表明，該方法能有效地診斷電動機軸承的早期故障，提高了船舶航行中的安全性。

[1]張 超,陳建軍,徐亞蘭.基于EMD分解和奇異值差分譜理論的軸承故障診斷方法[J].振動工程學報,2011,24:539-545. Zhang Chao,Chen Jianjun,Xu Yalan.A bearing fault diagnosis method based on EMD and difference spectrum theory of singular value[J].Journal of Vibration Engineering,2011,24:539-545.

[2]郭明威,倪世宏,朱家海.基于EMD-HMM的BIT間歇故障識別[J].振動、測試與診斷,2012,32:467-470. Guo Mingwei,Ni Shihong,Zhu Jiahai.Intermittent fault diagnosis for built-in test system based on EMD and HMM[J]. Journal of Vibration,Measurement&Diagnosis,2012,32(3):467-470.

[3]鄭軍林.EMD方法在內燃機故障診斷中的應用[J].內燃機,2012:55-58. Zheng Junlin.Application of EMD in internal combustion engine trouble-shooting[J].Internal Combustion Engines,2012: 55-58.

[4]Zhao Xiaomin,Patel T H,Zuo Ming J.Multivariate EMD and full spectrum based condition monitoring for rotating machinery[J].Mechanical Systems and Signal Processing,2012,27:712-728.

[5]時培明,丁雪娟,李 庚,等.一種EMD改進方法及其在旋轉機械故障診斷中的應用[J].振動與沖擊,2013,32(4):185-190. Shi Peiming,Ding Xuejuan,Li Geng,et al.An improved method of EMD and its applications in rotating machinery fault diagnosis[J].Journal of Vibration and Shock,2013,32(4):185-190.

[6]Kacha A,Grenez F,Benmahammed K.Time-frequency analysis and instantaneous frequency estimation using two-sided linear prediction[J].Signal Processing,2005,85:491-503.

[7]許同樂,張新義,裴新才,等.EMD遺傳神經網絡方法[J].北京郵電大學學報,2012,35(5):68-72. Xu Tongle,Zhang Xinyi,Pei Xincai,et al.EMD genetic neural networks method[J].Journal of Beijing University of Posts and Telecommunications,2012,35(5):68-72.

[8]胡勁松,楊世錫.EMD方法基于AR模型預測的數據延拓與應用[J].振動、測試與診斷,2007,27:116-120. Hu Jinsong,Yang Shixi.AR model prediction-based EMD method and its application to data extension[J].Journal of Vibration,Measurement&Diagnosis,2007,27(2):116-120.

[9]曹端超,康建設,趙勁松,等.EMD端點效應抑制方法仿真比較與實例分析研究[J].機械傳動,2013,(3):83-87. Cao Duanchao,Kang Jianshe,Zhao Jinsong,et al.Research on the comparison with methods of restraining ending effect of EMD and its application in fault diagnosis[J].Journal of Mechanical Transmission,2013,(3):83-87.

Study of bearing fault diagnosis method in marine engine

Xü Tong-le,GAO Peng-fei,CHEN Kang,HOU Meng-meng
(School of Mechanical Engineering,Shandong University of Technology,Zibo 255049,China)

An EMD method based on cross-correlation is proposed in view of the end effects and excessive false component of IMF.First,extension using cross-correlation analysis of non-stationary signal is applied to eliminate the end effect.Second,signal after eliminating end effect is decomposed with EMD,and keep the best IMF through cross-correlation between IMF and original signal.Finally,the Hilbert marginal spectrum of signal can be obtained and frequency feature is identified.The simulations reveal that the EMD method based on cross-correlation can solve the end effects perfectly and true IMF can be separated out effectively.The method is applied in rolling bearing faults diagnosis in marine engine.The result shows that the fault can be identified exactly.

EMD(Empirical Mode Decomposion);end effects;cross-correlation;fault diagnosis; IMF(Intrinsic Mode Function)

TP274

A

10.3969/j.issn.1007-7294.2016.08.012

1007-7294（2016）08-1028-08

2016-04-20

山東省自然科學基金計劃（ZR2013FM005）；山東省高等學校科技計劃項目（J10LG22）

許同樂（1965-），男，博士，教授，E-mail:xutongle@163.com；高朋飛（1988-），男，碩士研究生，E-mail:gpf_ok@163.com。