波浪水池中畸形波生成的研究綜述

鄧燕飛，楊建民，李 欣，肖龍飛

（上海交通大學 海洋工程國家重點實驗室，上海 200240）

波浪水池中畸形波生成的研究綜述

鄧燕飛，楊建民，李 欣，肖龍飛

（上海交通大學 海洋工程國家重點實驗室，上海 200240）

畸形波具有異常大的波高，容易對海洋結構物造成巨大破壞。世界各大海域均有畸形波發生及其引起的海難記錄，其生成機理正引起人們越來越多的關注。在實測畸形波時歷的基礎上，有必要在實驗室中實現畸形波的生成，從而揭示畸形波的生成機理及其對海洋結構物的作用機理。目前，國內外許多學者根據畸形波所產生的海洋環境條件提出了多種多樣的畸形波成因假說，并相應地形成了多種畸形波生成模型。色散聚集方法通過控制成分波相位使波浪能量定時定點聚集，簡單高效，仍為大多數的畸形波生成研究的首選。在此基礎上，部分學者提出或應用了迭代方法對畸形波模擬結果進行優化，以修正非線性波波作用引起的相位、幅值偏離。另一方面，薛定諤方程呼吸子解作為畸形波的一個原型，也在畸形波的生成模擬中得到成功應用。該文針對上述畸形波在數值波浪水池或物理水池中的模擬方法作了綜述，可為進一步開展畸形波的機理研究及其對海洋結構物作用機理研究提供基礎。

畸形波；生成模擬；波浪水池；綜述

0 引 言

隨著全球經濟的發展，陸上及近海的資源已經遠遠滿足不了人類的需求，深海油氣礦產資源開發越來越受到各國的重視。各種適應深海惡劣環境的浮式結構物不斷涌現，而如何確保結構物及人員的海上安全成為了海洋工程領域研究的重要課題。強非線性波浪可以引起海上結構物波浪爬升，抨擊等非線性問題發生，帶來極大的波浪載荷，是海上結構物安全的巨大威脅。

畸形波（Freak Wave）就是這樣一種強非線性極端波浪，具有波高極大，波峰突出，能量集中，破壞力大等顯著特征。1965年Draper[1]首次提出了畸形波的概念，此后畸形波這一現象及其對海上結構物的影響受到廣泛關注。人們又將畸形波稱為“深海怪獸”，形容其如同一面水墻，突然出現，然后很快消失得無影無蹤。目前，已發現畸形波廣泛存在于世界各個海域，可出現在深海和近海，風暴天氣和一般天氣，但以風暴天氣居多。

盡管畸形波的報道常常出現，但由于畸形波多在偶然情況下發生，海上實測存在很大困難，可依據的畸形波實測資料仍然匱乏。國內外學者對畸形波進行了多方面的探索，主要集中在畸形波生成機理、畸形波的模擬和畸形波對海洋結構物的強非線性作用上。畸形波可能會對海上結構物以及航行中的船舶帶來致命威脅，關于畸形波引起的海難記錄比比皆是[2-7]。研究人員希望通過在物理水池或數值水池中重現實測的畸形波時歷或生成符合畸形波定義的強非線性波浪時歷，以此研究畸形波的水動力特征以及其對結構物的非線性作用，從而為深入認識畸形波的生成機理，海上結構物的安全設計提供參考。

1 畸形波的特征及成因假說

1.1 畸形波特征

不同文獻中對畸形波的描述各有側重，但普遍認為畸形波具有一個突出的大波或者連續的幾個大波，波陡極陡且升高快，具有很強的非線性。

“新年波”是其中最著名的一個畸形波記錄，它是1995年1月1日15時20分在北海Draupner平臺被觀測到的最大波高達25.63 m的大波[8]。如圖1所示，新年波在水深為70 m的海域中發生，具有一個突出的大波。在長度為1 200 s的記錄中，有義波高為11.92 m，最大波高為有義波高2.15倍，波峰值達到18.5 m，該波浪嚴重損壞了挪威海域的Draupner石油平臺。此外，帶有連續幾個大波的波浪時歷，又稱三姐妹波（“Three Sister”wave），也是畸形波的一種常見的形式。Wolfram等人[9]對北阿爾文（North Alwyn）1994年至1998年的畸形波記錄進行統計分析，并對畸形波單波前后的波浪特征予以關注。分析顯示畸形波前后兩個波的波陡大約等于周圍波浪波陡有義值的一半，而前后兩個波的波高約等于有義波高，即一個畸形波時歷先后包含Hs，2*Hs，Hs三個波高的單波。

目前，畸形波并沒有一個明確的定義，普遍認為最大波高大于有義波高2倍的單波可以稱為畸形波[10]。

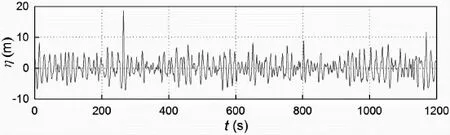
圖1 “新年波”波浪時歷Fig.1 New Year wave sequence

1.2 畸形波的成因假說

由于畸形波的發生不可預測，實測獲得的畸形波數據僅僅是某一位置的波浪升高時程，缺少畸形波演化發展過程的全面數據。迄今，針對畸形波的產生機理，學者們只能根據有限的實測數據，畸形波發生時的海況環境，提出多種的畸形波生成假說。Chien,Kao和Chuang[11]總結了前人的假說，并將其分成外部環境影響和波浪內部作用兩大類。其中，外部環境作用包括風暴能量持續輸送給波浪[12-13]、海底不平引起波浪變化[11,14]、反向流引起波浪的變形放大[15-17]以及波浪反射、折射或水深變化等引起的波浪能量集中[11]；波浪內部作用則包括波浪能量的線性疊加[18]以及波浪調制不穩定性引起的波群能量非線性自聚焦[19-20]等。

Mori,Liu和Yasuda[21]對日本海1986至1990年期間的實測波浪數據進行小波分析，發現在畸形波產生的過程中，波浪譜能量迅速集中并向高頻部分轉化。盡管對于畸形波的生成機理，眾說紛紜，但是這些假說無不與能量的轉移和集中有關。為了研究海上結構物在畸形波作用下的響應問題，研究人員廣泛采用能量集中方法，在物理水池或數值水池中使波浪能量在特定的時刻與地點匯聚，生成符合畸形波定義的能量高度集中的強非線性波浪。

2 畸形波在波浪水池生成研究進展

畸形波是海浪中的一種特殊現象。大量海上實測資料表明，海浪可以看作是平穩的，各態歷經的，具有高斯正態分布的隨機過程。根據Longuet-Higgins波浪模型[22]，深水波浪波高符合Rayleigh分布，其超值累積概率為：

根據畸形波的定義，令H/Hs=2.0，可以得到超值累計概率為3.35×10-4，即大約3 000個波浪中才出現一個符合畸形波定義的波浪。因此，通過隨機波浪理論生成畸形波的效率十分低下，而且畸形波出現的位置和時間無法預計，一般不予采用。

2.1 畸形波生成的色散聚焦模型

根據色散關系ω2=gktanh k（ ）h，不同波頻或波數的前進波在水中傳播時存在傳播速度不同的“色散”現象。在畸形波的生成模擬中，為了使波浪能量定點定時匯聚，可以使各成分波在某一位置同時達到最大值，疊加形成一個突出的大波。通常，在波浪水池中，可以先產生速度比較慢的短波，再產生速度快的長波，通過長波追上短波的方法，獲得符合畸形波定義的波浪。目前，基于色散聚集原理，學者們已經提出了多種在實驗室中生成畸形波的模型，并在數值或物理水池中實現。

2.1.1 瞬態波模擬

瞬態波的模擬由來已久，或是通過生成包含各頻率成分的波浪時歷，研究結構物在各頻率波浪下的響應問題，或是通過生成一個突出的接近破碎的大波，研究波浪破碎問題。Chaplin[23]總結了實驗室內通過聚焦手段生成瞬態波的三種方式，分別為相速度方法、逆傳播方法以及波群速方法。其中，最常用最方便有效的方法是相速度方法。

根據Longuet-Higgins波浪模型[22]，隨機波浪的分布可以表示為無數個隨機的正弦波浪線性疊加的形式，即

其中：N為組成波數目，An，kn，ωn，εn分別為第n個組成波的波幅、波數、圓頻率和隨機相位，An通過給定的波浪譜獲取則通過色散關系換算得到。為了使所有組成波在特定位置xc及特定時刻tc同時達到最大值，隨機相位εn可以設為εn=knxc-ωntc。這樣，波浪的分布可以描述為

Longuet-Higgins[24]采用這種方法在波浪水池中定點生成陡波，用來研究波浪破碎問題。Rapp和Melville[25]也同樣利用該方法生成接近破碎的波浪，研究波浪破碎過程中能量的耗散、波浪破碎極限等問題。Baldock,Swan和Taylor[26]研究了線性疊加生成的聚焦波浪下，波浪的運動學和動力學特征，并將實驗結果和線性理論、二階理論結果進行了對比。對比結果顯示，實驗生成的瞬態波具有更高更窄的波峰，且前后的波谷相對更寬更淺，呈現出強烈的非線性特征。

Tromans,Anaturk和Hagemeijer[27]提出了能夠模擬給定波峰值的瞬態波的“新波”（NewWave）理論。“新波”理論的標準型可以表達為波升值的自相關函數形式，即

式中：δω為能量譜的頻率間隔，σ2是波浪譜的方差。通過可以獲得與給定波峰值一致的瞬態波波浪升高的時程表達。引入空間變量x，單向入射波聚焦模型可以表示為

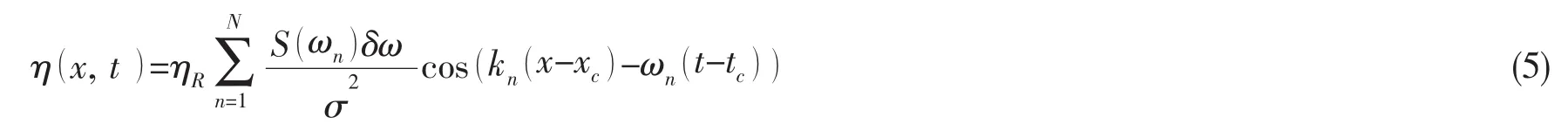
Johannessen和Swan[28]利用“新波”理論在實驗室中生成了三維瞬態波，并通過改變目標波峰值研究了瞬態波從接近線性到接近破碎的特征變化。Ning,Zang,Liu,Eatock Taylor,Teng和Taylor[29]在波浪水池中生成瞬態波，同時與考慮二階Stokes波的非線性數值波浪水池的模擬結果進行對比，結果顯示波-波非線性作用對畸形波的重要影響。Westphalen,Greaves,Williams,Zang和Taylor[30]則通過兩種商業軟件（STAR CCM+和CFX），建立速度入口的數值波浪水池，利用“新波”理論生成了瞬態波。

上述瞬態波的模擬是在波浪譜所有能量在特定位置特定時刻匯聚這一假設下進行的，這種假設帶來的后果是在聚焦前后波面近乎平靜，這與實際情況是不符的。為了使畸形波的模擬與隨機海況一致，學者們在瞬態波的模擬上增加了背景波浪成分。

2.1.2 波列組合模型

目前，在實驗室中大部分的畸形波模擬實驗是基于雙波列組合模型開展的。雙波列組合模型是基于瞬態波的模擬方法，把部分成分波的能量或者成分波中的部分能量分配到背景波浪中，使生成的畸形波與實際海況相符，同時保持波浪譜的統計特性（如有義波高、譜峰周期）與目標值一致。

（1）約束式“新波”理論

Cassidy[31]通過把“新波”嵌入到隨機波浪中，并保持聚焦時刻的波峰值和波升值梯度（即為0）不變，得到約束式“新波”理論。在聚焦位置處，波浪的時程表達為

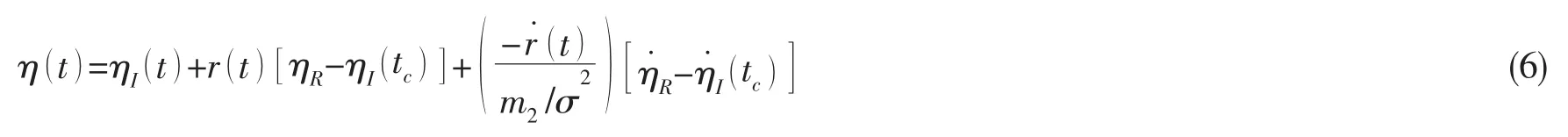
其中：m2為波浪譜的二階矩。

（2）Kriebel雙波列組合模型

Kriebel和Alsina[18]提出了在真實背景波浪中嵌入瞬態波以生成符合真實海況的畸形波的方法。該模型組合了利用隨機相位生成的隨機波和利用人工干預相位生成的瞬態波，即

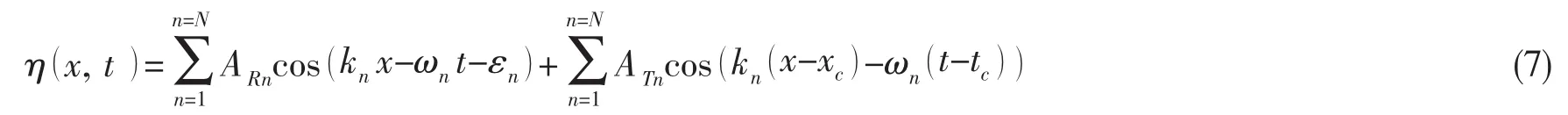
Kriebel和Alsina[18]利用上述組合模型在物理水池中生成畸形波時歷，結果顯示，只需要15%的能量進入瞬態波時歷，即可生成與海上觀察到的畸形波相符的波浪時歷，且模擬的波浪能量譜與目標譜接近。由于該模型思路清晰，實現容易，模擬效果較好，因而在物理水池和數值波浪水池生成畸形波中被廣泛采用[32]。

為了提高畸形波模擬生成的概率，同時嚴格控制瞬態波的能量配比以免模擬波浪譜的統計值偏離目標值，Hu,Tang和Xue[33]基于概率分析，研究了Kriebel組合模型下組成波數對畸形波模擬出現概率的影響，并在數值波浪水池中利用較小的瞬態波能量配比生成了畸形波。研究顯示，在某一PM譜下，基于上述組合模型生成畸形波的概率可表達為

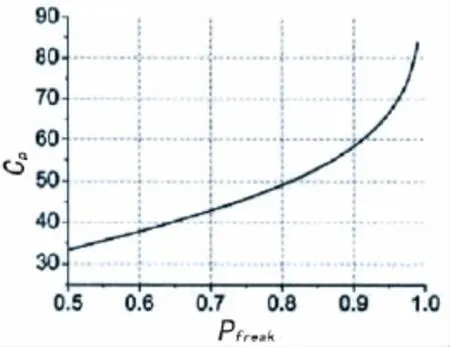
圖2 畸形波模擬生成概率與參數Cp的關系曲線Fig.2 Relationship between simulated occurrence probability of freak waves and parameter Cp

其中：erf為誤差函數，γ=ηmin/ηmax取決于ωm，且在ωm＜2 rad/s時變化范圍不大。令（N為組合波數），可得到畸形波生成概率與Cp的關系曲線，如圖2所示。

（3）三波列組合模型

裴玉國[14]基于Kriebel的組合模型，提出了一個三波列組合模型，將目標譜能量分配到一個隨機波列和兩個瞬態波列中，即

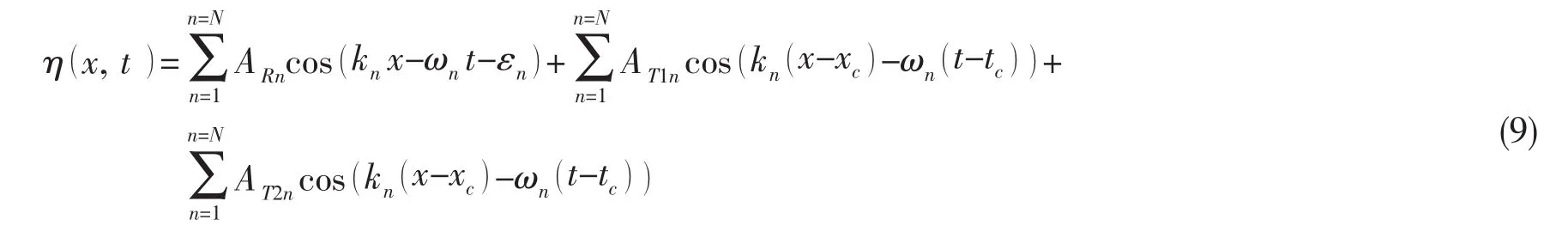
在物理水池中，分別基于雙波列和三波列組合模型模擬畸形波，對比結果顯示當瞬態波能量配比相同時，三波列組合模型生成的畸形波波高更大，非線性更強，提高了畸形波模擬的效率。

（4）部分組成波聚焦模型

趙西增[34]針對在有限空間和時間內模擬出畸形波，提出了有效模擬畸形波的部分組成波聚焦模型。在組成波的隨機初相位非均勻分布的條件下，使部分組成波構成背景波浪，另外一部分組成波在給定的時間和位置聚焦，從而達到在隨機波列中模擬畸形波的目的

其中：N1是構成背景波的組成波數目，N-N1是用于聚焦瞬態波的組成波數目。

2.1.3 相位調制模型

上述波列組合模型，均是通過在背景波浪中嵌入完全聚焦的瞬態波來實現。為了生成滿足畸形波定義的波浪，在前人研究的基礎上，人們又提出通過調制各組成波的相位，使較多的波浪能量在給定的時間和位置匯聚，從而形成一個大波，此為相位調制模型。

趙西增[34]通過調制相位角的分布范圍，使各組成波的初相位分布在相對狹窄的范圍內，從而提高隨機波列中模擬得到畸形波的概率

式中：εn為第n個組成波的初相位，在內均勻隨機分布，α為內的常數。一般來說，α越小，各組成波的能量就分布在越狹窄的空間內，從而更容易生成畸形波。

此后，劉贊強[35]在部分組成波聚焦模型和相位調制模型的基礎上，提出了新的相位調制方法。該調制方法的波面表達形式為

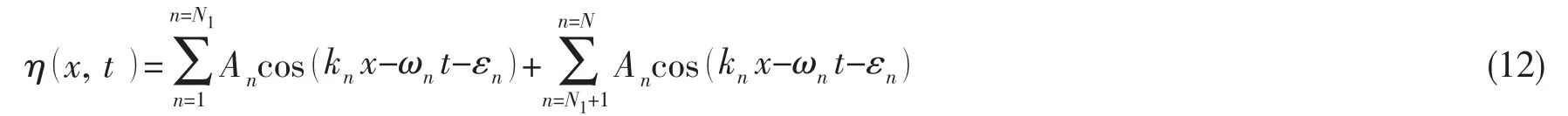
其中：上式第二項為調制聚焦項，當n＞N1時，利用調制N-N1個組成波的初相位εn，使其滿足Ancos（ knxωnt-εn）＞0。通過基于純線性理論的數值模擬對比，結果顯示新的相位調節模型生成畸形波效率高，相位分布隨機性好，模擬結果具有微調性。基于上述新的相位調制方法，劉贊強[35]在物理水池中模擬了“新年波”、日本海畸形波等實測畸形波時歷，證明了該方法實現實測畸形波的物理生成的有效性。

2.1.4 特定畸形波時歷的生成

由于畸形波的出現不可預測且持續時間短，現有的“新年波”、北海畸形波等實測資料均是在某一點的波面時程記錄。通過數值波浪水池或物理水池復演實測畸形波時歷，有助于分析畸形波的生成演化過程以及其動力學特征。

Liang,Yang,Li和Li[36]通過把特定的波浪時歷分解成一系列規則波的疊加形式，繼而得到造波板處的波浪升高，并轉化成造波板運動信號，實現了給定瞬態波時歷在數值波浪水池的模擬。對于給定的不規則波時歷根據Longuet-Higgins波浪模型[22]，可以表示成

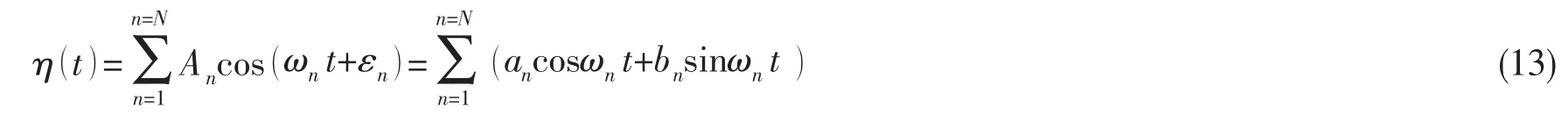
其中：

通過使目標函數獲得最小值，可以得到系數an、bn的表達式：

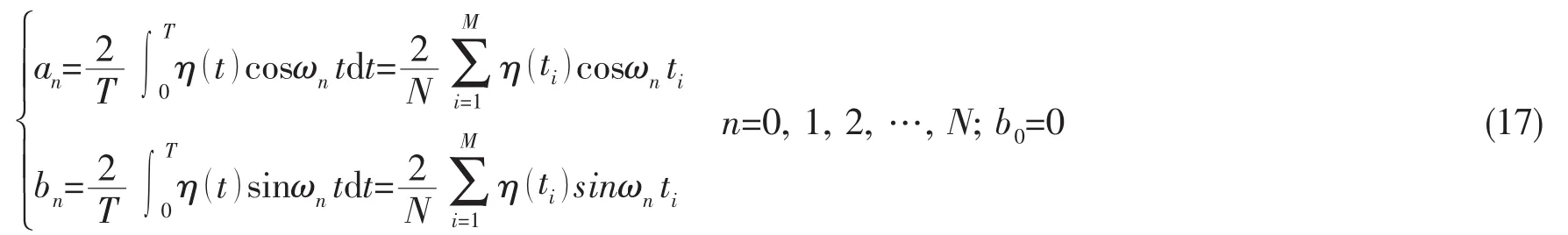
崔成[37]通過傅里葉分解包含“新年波”的實測波面時歷，獲得如（13）式表示的各組成波疊加的形式，從而確定數值造波的邊界條件，在數值波浪水池中模擬得到與實測“新年波”時歷較為符合的結果。如圖3所示，模擬的“新年波”時歷與實測時歷保持一致，最大波高與有義波高比值Hmax/Hs為2.28，與實測值2.15相近，而最大波峰與最大波高比值ηmax/Hmax為0.72，與實測值相符。可見，利用此方法生成特定的畸形波時歷有較好的效果。

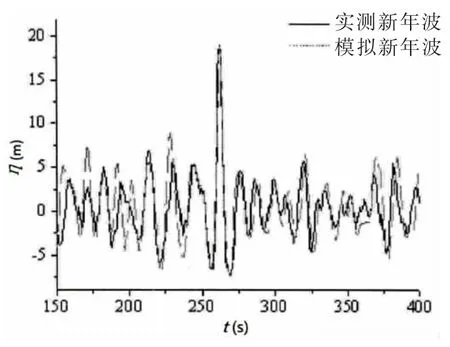
圖3 實測和模擬的“新年波”時歷對比Fig.3 Comparison of the recorded(solid line)and numerical(dash line)New Year wave sequences

2.1.5 色散聚焦的二階修正

線性疊加理論是真實波浪環境的一種近似。對于波高較大，水深較淺的情況，采用更加準確的二階理論能夠在一定程度上提高波浪模擬的精度和效率。

對于采用速度入口的數值波浪水池，根據Stokes波浪理論，可在入口邊界上直接輸入二階波面升高和二階速度剖面生成波浪時歷。Ning,Zang,Liu,Eatock Taylor,Teng和Taylor[29]采用二階Stokes波浪理論，在數值波浪水池中生成聚焦波浪，并對其演化過程及運動學特征進行了分析。

在實驗室中，通過推板或搖板進行仿物理造波時，造波板附近將會產生自由子諧波或高階諧波，這些諧波會極大地干擾波浪的聚焦過程。Madsen[38]給出了推板造波運動公式的近似修正，用于消除規則波中的自由波成分，避免在波浪傳播過程中由于自由波相速與主波差異導致的波形不穩定。實驗證明，在的范圍內，利用修正后的二階推板運動公式，如下式，可以產生具有穩定波形的Stokes二階波。

其中：

S0為推板沖程，h0為水深，a為波幅。查晶晶[39]采用Madsen二階造波理論，在數值波浪水池中生成了具有穩定波形的Stokes二階波浪，如圖4所示。

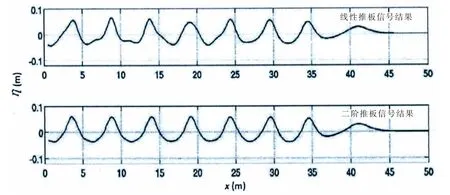
圖4 推板線性和二階造波運動波面曲線對比（t=21.8 s時刻）Fig.4 Comparison of wave elevations with linear and second-order wave maker signals(t=21.8s)

Sch?ffer[40]推導了一種改進的二階控制信號，用于減少造波板附近衍生的自由子諧波或高階諧波。通過增加一個二階信號，加入Longuet-Higgins和Stewart[41]提出的反向散射驅動信號中，以消除自由波的影響，能夠達到生成穩定的聚焦波的目的。然而，這一方法的較復雜且計算量大。Schlurmann, Lengricht和Graw[42]采用Sch?ffer[43]提出的漸近合成法在物理水池中生成了瞬態波，并利用particle image velocity（PIV）方法研究了波浪破碎時波峰下水質點的速度和加速度分布情況。

2.2 畸形波生成的迭代優化方法

為了研究浮體結構在特定波浪中的響應問題，如傾覆試驗，抨擊研究等，在物理水池或數值波浪水池中生成具有特定波形和局部波浪特征的波浪是有重要意義的。為了實現這一目的，學者們先后提出了相位—幅值迭代模型和優化波模型。

3.2.1 相位—幅值迭代法

根據Longuet-Higgins波浪模型[22]，任意波浪時歷可以分解成足夠多的規則波疊加的形式，即組成規則波的相位譜和幅值譜直接決定了波浪時歷的形態和大小。在實驗室造波時，由于波浪在傳播過程中存在各種各樣的非線性因素，其在采樣位置的波浪時歷不可能與基于線性理論的結果完全一致。因此，有必要調整組成波的相位、幅值，使在采樣位置的波浪時歷不斷接近目標時歷。

Chaplin[23]在生成瞬態波的研究中，首先提出了相位迭代的方法，即通過測量相位譜與目標相位譜對比，調整造波板運動的相位信息。相位迭代過程如下表述

式中：φold為初始造波板控制信號或上一次造波板控制信號的相位角，φnew為新的造波板控制信號相位角，φrecorded則為實驗得到的波浪時歷組成波相位角，φtarget為目標波浪時歷組成波的相位角。

Schmittner,Kosleck和Hennig[44]在相位迭代方法的基礎上，提出了相位—幅值迭代模型，對組成波的幅值也進行相應的迭代優化，使生成的畸形波的波峰值不斷接近目標時歷的波峰值。相位—幅值迭代模型同樣通過（21）式進行相位優化，同時，通過下式優化聚焦波浪的波峰值：

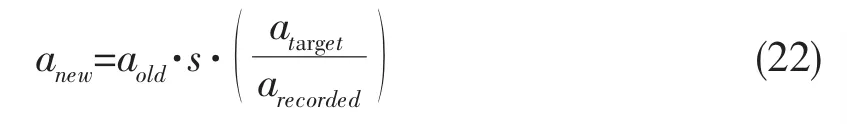
式中：aold為初始造波板控制信號或上一次造波板控制信號的對應各組成波的幅值，anew為新的造波板控制信號幅值，arecorded則為實驗得到的波浪時歷組成波幅值，atarget為目標波浪時歷組成波的幅值。s為比例因子，用于加速迭代過程，而當測量波浪幅值譜接近目標譜時，s設為1。Schmittner,Kosleck和Hennig[44]利用上述相位-幅值迭代方法在物理水池中生成了與目標時歷接近的波浪時歷，迭代優化過程獲得的波浪時歷對比如圖5所示。

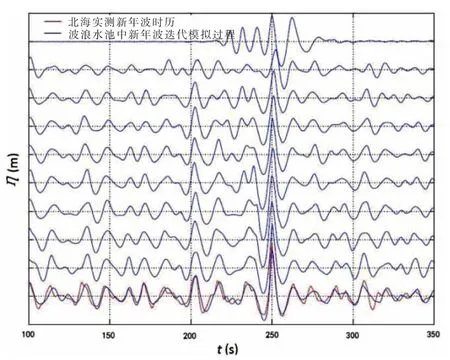
圖5 特定波浪時歷模擬優化過程結果對比Fig.5 Wave elevation results of deterministic wave sequence among iteration process

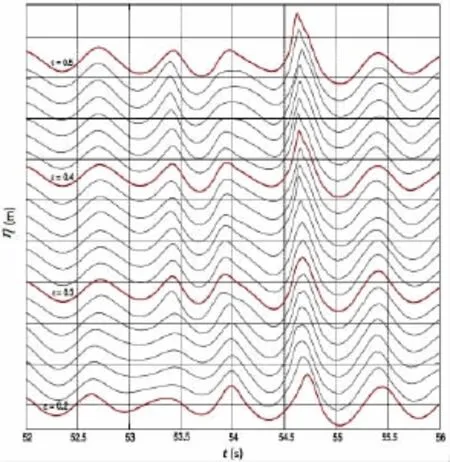
圖6 特定峰前波陡波浪時歷迭代優化模擬結果對比Fig.6 Wave elevation results of specific wave front steepness among iteration process

2.2.2 優化波法（Optimized wave）

在研究非線性波浪對結構物的相互作用時，往往需要設計并生成具有不同波形的波浪時歷。對于給定波浪能量譜的情況，組成波的相位譜將唯一地確定波浪時歷的局部特征參數，例如波高、周期和最大波出現的時間和地點。為了在實驗室中生成特定局部特征參數的波浪時歷，Clauss和Steinhagen[45]建立了一個目標波浪參數模擬的約束優化模型，并利用序列二次規劃法（Sequential Quadratic Programming）獲得約束優化模型關于相位譜的最優解，從而生成造波板的控制信號。Clauss和Steinhagen[45]在有限元數值波浪水池中采用優化后獲得的造波板控制信號，生成了與目標參數包括峰前波陡和最大波高等接近的波浪時歷。盡管這一優化過程是基于線性理論的，但其與數值波浪水池結合能夠有效地模擬給定目標參數的波浪時歷，且考慮了造波機的造波能力。

Steinhagen[46]在上述約束優化模型的基礎上，針對在數值波浪水池中進行波浪的非線性模擬，采用一種改進的simplex方法[47]對畸形波的非線性模擬結果進行迭代優化，并引入小波變換（wavelet transform）方法減少迭代優化過程的計算量。這種首先利用序列二次規劃法迭代優化獲得造波板運動的初始信號，再通過subplex法（即改進的simplex法）對物理水池或數值波浪水池中波浪的非線性模擬結果進行迭代優化的方法稱為優化波法。

Clauss[48]利用優化波法在物理水池和數值水池中重演了新年波（New Year Wave）、Yura波以及三姐妹波（“Three Sisters”wave）。Clauss,Schmittner和Klein[49]通過此方法生成具有特定波陡的畸形波波浪時歷，迭代模擬過程如圖6所示。經過優化，最終獲得的峰前波陡達到0.49，接近破碎的極限。

2.3 基于薛定諤方程呼吸子解生成畸形波

對于畸形波的生成機理，很多學者都將其與波浪調制不穩定性關聯在一起[50]。最初，學者們在研究中發現Stokes波對于緩慢調制的周期性（邊帶）擾動是不穩定的，即速度和波長有微小差別的幾個波列的共振相互作用涉及近正弦波的緩慢調制，波列之間會發生能量交換。Benjamin和Feir[51]對這一事實作了關鍵性的論證工作，證實深水波列傳播過程中演化具有不穩定性。Whitham[52]給出了一對非線性守恒型方程，證實并推廣了不穩定性理論。這與后來Zakharov[53]基于窄譜假設和弱非線性假設，推導得到的描述波包絡演化的三階非線性薛定諤方程是一致的。深水條件下三階非線性薛定諤方程如下式表示：

其波面升高由下式獲得

式中：k0和ω0分別為載波波數和波頻。對于深水波，波包絡以二分之一相速度的群速度cg=ω0/ 2k0向前傳播。

薛定諤方程存在一系列能夠描述波浪強非線性聚焦的呼吸子解，其中Peregrine呼吸子解描述了Stokes波在無限長調制波長情況下調制不穩定的非線性階段。鑒于畸形波有著極大的波高，且突然出現又迅速消失，這一特征與Peregrine呼吸子解非常相似，許多學者都將Peregrine呼吸子解作為畸形波產生的原型[54-55]。三階薛定諤方程的Peregrine呼吸子解如下式表示：

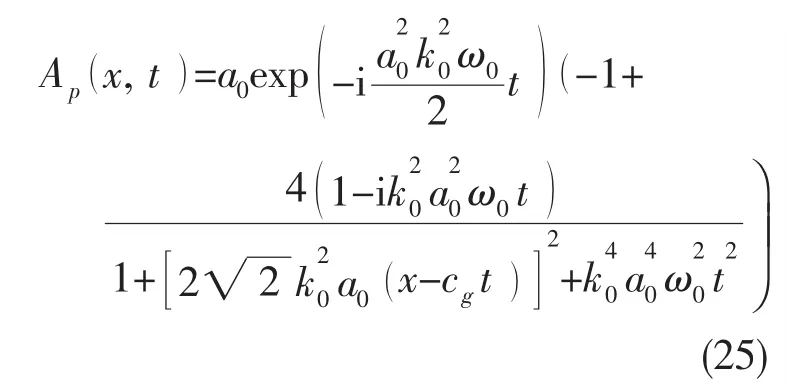
近年來，已有學者在物理水池或數值波浪水池中利用Peregrine呼吸子解給定的波面條件，實現了單一載波頻率下畸形波的生成[56-59]。利用Peregrine呼吸子解生成畸形波的關鍵在于確定造波板的控制信號。理論上，造波板運動應確保靠近造波板處的波浪升高與Peregrine呼吸子解給出的造波板處波面歷程完全一致。Chabchoub,Hoffmann和Akhmediev[56]通過使造波板位移與成正比，獲得與理論值十分接近的波浪時歷，如圖7所示。因而，這一確定造波板運動的簡化方法是有效的，造波板運動可通過下式決定：

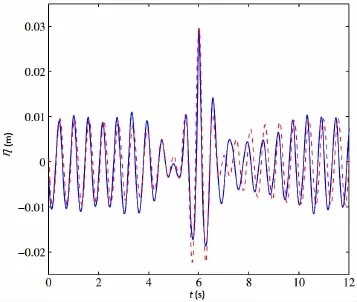
圖7 利用Peregrine呼吸子解在水池中生成的畸形波時歷（實線）與理論值（虛線）對比Fig.7 Comparison of the simulated(solid line)and theoretical (dash line)wave elevations based on Peregrine breather solution

3 結 語

近年來，畸形波的研究在國內已引起了廣泛的關注，并在理論研究、實驗室模擬和數值模擬上取得了較大的進展。針對畸形波在物理水池或數值波浪水池中的生成模擬，在閱讀大量文獻的基礎上，本文綜合分析了國內外實現畸形波模擬的波浪模型或生成方法。基于實用性的考慮，目前國內外生成畸形波的方法主要基于色散聚焦，部分研究通過迭代優化組成波的相位分布，改善了波浪的聚焦效果。另一方面，基于波浪傳播過程中的邊帶不穩定性理論，國內外一部分研究基于薛定諤方程呼吸子解實現了在物理水池或數值模擬中生成畸形波。值得注意的是，學術界目前對畸形波的發生機理尚未有統一認識。根據實測畸形波資料，畸形波較多地發生在強風暴天氣或存在反向流海域。盡管強風暴及反向流對畸形波的生成影響已有較多的理論研究，然而在波浪水池中驗證研究尚未能見到。在物理或數值的風浪流水池中，對這方面的理論進行實驗研究，對揭示畸形波生成機理有著重要的意義。此外，畸形波對海洋運載器及浮式結構的破壞并不少見，其對海洋結構物的作用機理尚不明晰。海上安全事故一旦發生，損失將十分慘重。針對畸形波對海洋結構物的強非線性作用（如爬升、抨擊及大幅度運動響應等）亟待深入的研究。

[1]Draper L.Freak wave[J].Marine Observer,1965,35(2):193-195.

[2]Schulz M.Ichspürte den atemgottes[J].Der Spiegel,2001(51):208-216.

[3]Clauss G F,Schmittner C E,Hennig J.Systematically varied rogue wave sequences for the experimental investigation of extreme structure behavior[J].Journal of Offshore Mechanics and Arctic Engineering,2008,130(2).

[4]Kharif C,Pelinovsky E,Slunyaev A.Rogue waves in the ocean[M].Springer Berlin Heidelberg,2009.

[5]Bertotti L,Cavaleri L.Analysis of the voyager storm[J].Ocean Engineering,2008,35(1):1-5.

[6]Lemire J.Freak wave rocks cruise[J].New York Daily News,2005.

[7]Monbaliu J,Toffoli A.Regional distribution of extreme waves[C]//Proceedings of Maxwave final meeting.Genève,2003.

[8]Haver S,Anderson O J.Freak waves:Rare realizations of a typical population or typical realizations of a rare population [C]//Proceedings of the 10th International Offshore and Polar Engineering Conference.Seattle,USA,2000:123-130.

[9]Wolfram J,Linfoot B,Stansell P.Long-and short-term extreme wave statistics in the North Sea:1994-1998[C].Proceedings of Rogue Wave 2000,2000:363-372.

[10]Kjeldsen S P.Measurements of freak waves in norway and related ship accidents[C]//Proceedings of Royal Institution of-Naval Architects International Conference-Design and Operation for Abnormal Conditions III.London,UK,2005:31-38.

[11]Chien H,Kao C C,Chuang L Z H.On the characteristics of observed coastal freak waves[J].Coastal Engineering Journal, 2002,44(4):301-319.

[12]Kharif C,Giovanangeli J P,Touboul J,et al.Influence of wind on extreme wave events:experimental and numerical approaches[J].Journal of Fluid Mechanics,2008,594:209-247.

[13]Donelan M,Magnusson A.The role of meteorological focusing in generating rogue wave conditions[C]//Proceedings of Aha Huliko’a Hawaiian Winter Workshop.University of Hawaii at Manoa,2005:139-145.

[14]裴玉國.畸形波的生成及基本特性研究[D].大連:大連理工大學,2007. Pei Yuguo.The generation of freak waves and its behaviors[D].Dalian:Dalian University of Technology,2007.

[15]White B S,Fornberg B.On the chance of freak waves at sea[J].Journal of Fluid Mechanics,1998,355:113-138.

[16]Lavrenov I,Porubov A.Three reasons for freak wave generation in the non-uniform current[J].European Journal of Mechanics-B/Fluids,2006,25(5):574-585.

[17]Wu C H,Yao A.Laboratory measurements of limiting freak waves on currents[J].Journal of Geophysical Research,2004, 109,C12002.

[18]Kriebel D L,Alsina M V.Simulation of extreme waves in a background random sea[C]//Proceedings of the 10th International Offshore and Polar Engineering Conference.Seattle,USA,2000,3:31-37.

[19]Dyachenko A,Zakharov V E.Modulation instability of stokes wave→Freak wave[J].JETP letters,2005,81(6):255-259.

[20]Zakharov V E,Dyachenko A,Prokofiev A.Freak waves as nonlinear stage of stokes wave modulation instability[J].European Journal of Mechanics-B/Fluids,2006,25(5):677-692.

[21]Mori N,Liu P C,Yasuda T.Analysis of freak wave measurements in the sea of Japan[J].Ocean Engineering,2002,29 (11):1399-1414.

[22]Longuet-Higgins M S.On the statistical distributions of sea waves[J].J mar Res,1952,11(3):245-265.

[23]Chaplin J R.On frequency-focusing unidirectional waves[J].International Journal of Offshore and Polar Engineering,1996, 6(02):131-137.

[24]Longuet-Higgins M.Breaking waves in deep or shallow water[C]//Proceedings of the 10th Conference on Naval Hydrodynamics MIT.Cambridge,USA,1974:597-605.

[25]Rapp R,Melville W.Laboratory measurements of deep-water breaking waves[J].Philosophical Transactions of the Royal Society of London,Series A:Mathematical and Physical Sciences,1990,331(1662):735-800.

[26]Baldock T,Swan C,Taylor P.A laboratory study of nonlinear surface waves on water[J].Philosophical Transactions of the Royal Society of London,Series A:Mathematical,Physical and Engineering Sciences,1996,354(1707):649-676.

[27]Tromans P S,Anaturk A R,Hagemeijer P.A new model for the kinematics of large ocean eaves-application as a design wave[C]//Proceedings of the First International Offshore and Polar Engineering Conference.Edinburgh,UK,1991,3:64-71.

[28]Johannessen T B,Swan C.A laboratory study of the focusing of transient and directionally spread surface water waves[J]. Proceedings of the Royal Society of London,Series A:Mathematical,Physical and Engineering Sciences,2001,457(2008): 971-1006.

[29]Ning D,Zang J,Liu S,et al.Free-surface evolution and wave kinematics for nonlinear uni-directional focused wave groups[J].Ocean Engineering,2009,36(15):1226-1243.

[30]Westphalen J,Greaves D,Williams C,et al.Numerical simulation of extreme free surface waves[C]//Proceedings of the 8th International Offshore and Polar Engineering Conference&Exhibition.Vancouver,BC,Canada,2008:55-61.

[31]Cassidy M J.Non-linear analysis of jack-up structures subjected to random waves[D].Oxford:University of Oxford,1999.

[32]劉曉霞.三維波浪場中畸形波的數值模擬[D].大連:大連理工大學,2008. Liu Xiaoxia.Numerical simulation of freak waves in three-dimensional wave field[D].Dalian:Dalian University of Technology,2008.

[33]Hu Z,Tang W,Xue H.A probability-based superposition model of freak wave simulation[J].Applied Ocean Research, 2014,47:284-290.

[34]趙西增.畸形波的實驗研究和數值模擬[D].大連:大連理工大學,2008. Zhao Xizeng.Experimental and numerical study of freak waves[D].Dalian:Dalian University of Technology,2008.

[35]劉贊強.畸形波模擬及其與核電取水構筑物作用探究[D].大連:大連理工大學,2011. Liu Zanqiang.Freak wave simulation and its interaction with nuclear power station ingarage structure[D].Dalian:Dalian University of Technology,2011.

[36]Liang X,Yang J,Li J,et al.A numerical study on local characteristics of predetermined irregular wave trains[J].Ocean Engineering,2011,38(4):651-657.

[37]崔 成.畸形波生成,演化及內部結構研究[D].大連:大連理工大學,2013. Cui Cheng.Study on generation,evolution and internal structures of freak waves[D].Dalian:Dalian University of Technology,2013.

[38]Madsen O S.On the generation of long waves[J].Journal of Geophysical Research,1971,76(36):8672-8683.

[39]查晶晶.基于Openfoam的數值造波與消波模型及其應用[D].上海:上海交通大學,2011.Zha Jingjing.Numerical model of wave generation and absorption based on openFOAM and its applications[D].Shanghai: Shanghai Jiao Tong University,2011.

[40]Sch?ffer H A.Second-order wavemaker theory for irregular waves[J].Ocean Engineering,1996,23(1):47-88.

[41]Longuet-Higgins M S,Stewart R.Changes in the form of short gravity waves on long waves and tidal currents[J].Journal of Fluid Mechanics,1960,8(04):565-583.

[42]Schlurmann T,Lengricht J,Graw K U.Spatial evolution of laboratory generated freak waves in deep water depth[C]//Proceedings of the 10th International Offshore and Polar Engineering Conference.Seattle,USA,2000,3:54-59.

[43]Sch?ffer H.The influence of evanescent modes in second order wave generation[C].Proceedings of Waves-Physical and Numerical Modeling,1994.

[44]Schmittner C,Kosleck S,Hennig J.A Phase-amplitude iteration scheme for the optimization of deterministic wave se quences[C]//Proceedings of the ASME2009 28th International Conference on Ocean,Offshore and Arctic Engineering. Honolulu,Hawaii,USA,2009:653-660.

[45]Clauss G F,Steinhagen U.Optimization of transient design waves in random sea[C]//Proceedings of the 10th International Offshore and Polar Engineering Conference.Seattle,USA,2000,3:229-236.

[46]Steinhagen U.Synthesizing nonlinear transient gravity waves in random seas[D].Technische Universit?t Berlin,2001.

[47]Rowan T H.Functional stability analysis of numerical algorithms[D].Austin:University of Texas,1990.

[48]Clauss G F.Task-related rogue waves embedded in extreme seas[C]//Proceedings of the 21st International Conference on Offshore Mechanics and Arctic Engineering.Oslo,Norway,2002:653-665.

[49]Clauss G F,Schmittner C E,Klein M.Generation of rogue waves with predefined steepness[C]//Proceedings of OMAE 2006 25th International Conference on Offshore Mechanics and Arctic Engineering.Hamburg,Germany,2006,2:319-325.

[50]Kharif C,Pelinovsky E.Physical mechanisms of the rogue wave phenomenon[J].European Journal of Mechanics-B/Fluids,2003,22(6):603-634.

[51]Benjamin T B,Feir J.The disintegration of wave trains on deep water Part 1.Theory[J].Journal of Fluid Mechanics, 1967,27(03):417-430.

[52]Whitham G.Non-linear dispersion of water waves[J].Journal of Fluid Mechanics,1967,27(02):399-412.

[53]Zakharov V E.Stability of periodic waves of finite amplitude on the surface of a deep fluid[J].Journal of Applied Mechanics and Technical Physics,1968,9(2):190-194.

[54]Shrira V I,Geogjaev V V.What makes the peregrine soliton so special as a prototype of freak waves[J].Journal of Engineering Mathematics,2010,67(1-2):11-22.

[55]Akhmediev N,Ankiewicz A,Taki M.Waves that appear from nowhere and disappear without a trace[J].Physics Letters A,2009,373(6):675-678.

[56]Chabchoub A,Hoffmann N,Akhmediev N.Rogue wave observation in a water wave tank[J].Physical Review Letters, 2011,106(20):204502.

[57]Chabchoub A,Akhmediev N,Hoffmann N.Experimental study of spatiotemporally localized surface gravity water waves [J].Physical Review E,2012,86(1):016311.

[58]Peric R,Hoffmann N,Chabchoub A.Initial wave breaking dynamics of peregrine-type rogue waves:A Numerical and Experimental Study[J].arXiv preprint arXiv:14010949,2014.

[59]Chabchoub A,Hoffmann N,Branger H,et al.Experiments on wind-perturbed rogue wave hydrodynamics using the peregrine breather model[J].Physics of Fluids,2013,25(10):101704.

A review on the freak wave generation in the wave tank

DENG Yan-fei,YANG Jian-min,LI Xin,XIAO Long-fei
(State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China)

Freak waves,a kind of extremely high waves,are very likely to cause great damage to offshore structures.The occurrence of freak waves and the damages they had caused have receiving more and more attentions.On the basis of freak wave registrations,it is necessary to generate freak wave sequences in the laboratory in order to reveal the formation mechanisms of freak waves and their impacts on offshore structures.At present,various formation hypotheses were proposed according to the sea states of freak wave occurrences and the corresponding simulation methods were produced.The most common approach is based on the dispersion focusing.This method is simple and effective to converge the wave energy at a fixed moment and location by adjusting phases of wave components.Iteration schemes were also put forward and successfully implemented to optimize the freak wave simulations.On the other hand,the Peregrine breather solution of Schr?dinger equation was also successfully simulated as a prototype of freak wave.This paper presents a state-of-art review on the above freak wave generation models,which were successfully implemented in numerical wave tank or physical wave tank.

freak waves;wave generation;wave tank;review

U661.7

A

10.3969/j.issn.1007-7294.2016.08.015

1007-7294（2016）08-1059-12

2016-03-15

國家自然科學基金重點項目（51239007）

鄧燕飛（1989-），男，博士研究生；楊建民（1958-），男，教授，博士生導師，通訊作者，E-mail:jmyang@sjtu.edu.cn。