讓數學課堂因追問而精彩

李楨

摘 要：問題是數學的心臟，本文通過教學案例，論述了如何在示錯教學中通過教師的有效追問，讓數學課堂更具有效性.

關鍵詞：示錯教學；有效追問；立體幾何

美國數學家哈爾莫斯說：“問題是數學的心臟”. 在課堂教學中，教師作為學生學習的合作者、組織者和引導者，每一個提問都應對學生的數學學習起到較好的導向作用. 在示錯教學中，面對學生的錯誤，進行有效追問是很好的處理辦法.數學課堂將因教師的追問而綻放光彩.

“示錯”是指展示錯誤，即教師通過適當的形式，暴露學生的錯誤，并挖掘錯因，通過尋找、分析、彌補、修正等過程，幫助學生理解并逐步改正錯誤，并以此為載體，加深對數學知識本質的理解和數學基本方法的掌握. “追問”，是指追根究底地問，即教師針對某一內容或某一問題，為使學生弄懂弄透，結合學生對問題的理解程度，環環相扣地提問，讓問題不斷深入，直到學生能夠充分理解.

在數學課的示錯教學中，有效追問不僅能幫助學生在改正錯誤的過程中逐步將知識內化，還能提升學生的學習熱情，激活學生的數學思維，調動學生學習的積極性和思考的主動性，提升課堂的有效性. 本文將通過具體的教學案例說明有效追問在示錯教學中的運用.

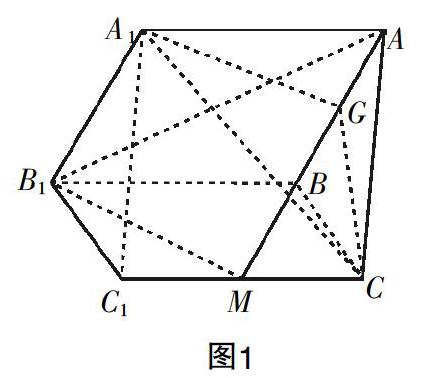
案例 在直三棱柱ABC-A1B1C1中，點M為CC1的中點，G是棱AB上的動點. 若CG∥面AB1M，試確定G的位置，并給出證明.

學生錯誤：先指出點G的位置，再根據點G的位置去證明CG∥面AB1M，這是不嚴謹的.

追問過程：

結合學生的上述錯誤，教師通過學生的回答，暴露學生的錯誤，并設計了如下問題，與學生一起研究.

老師問：本題的CG∥面AB1M是已知條件，還是結論？

學生1：是已知條件，（思考片刻），好像我那樣做錯了，因為我把它當作結論去證明了（從語氣上看，還是比較猶豫）.

學生2：我認為先指出點G為中點，再去證明CG∥面AB1M也是可以的. 我們通過猜測，估計點G是AB的中點，并給出了證明.

學生3：我覺得生2的做法不對，他把條件和結論顛倒了.

（此時，班級的學生分成兩派意見，有贊成這種做法的，也有反對的，但是理由都不能讓對方信服.）

追問1：既然CG∥面AB1M是條件，那么，從已知條件，你能知道點G的位置是否唯一嗎？

學生4：不能，因為過點C可以作無數條直線與平面AB1M平行，因此先猜測點G的位置是有缺陷的，可能會漏掉其他位置的點G也滿足題意. 還是應該把CG∥面AB1M當作已知條件去做. （所有學生都表示贊同，剛才的爭論也算解決了）

追問2：把CG∥面AB1M作為已知條件，你能聯想到什么知識？

學生5：線面平行的性質定理. 過CG作平面CGPM與平面AB1M有交線MP，則CG∥MP，而M是CC1的中點，利用MCGP為平行四邊形可以知道GP MC BB1，PG為△AB1B的中位線，G為中點.

追問3：如何說明MCGP為平行四邊形？

學生5：先根據線面平行的性質定理，可得CG∥MP，再用一次線面平行的性質定理，可得CM∥GP.

學生6：也可以過點G作PG∥BB1，PG交AB于點P. 易得CGPM是平行四邊形.

追問4：從剛才的過程，我們知道，過CG作一個平面與平面AB1M相交是關鍵，那么這樣的平面是否一定需要過點M？

（學生若有所思，紛紛表示有自己的方法想與大家交流）

學生7：不一定，我們可以作平面GAC與平面AB1M相交，其中一個交點是A，只需確定另一個交點. （該生不知道另一個交點怎么確定）

學生8：（補充學生7的回答）延長BC，B1M交于一點Q，連結AQ，則CG∥面AB1Q，可得GC∥AQ. 又因為點C為BQ的中點，所以CG是△ABQ的中位線.

（此時，一個學生舉手了，也許受到剛才的方法的啟發）

學生9：也可以直接利用平面A1GC與平面AB1M相交，記A1G與AB1交于T，A1C與AM交于S，則ST∥GC，由相似比可得G為AB中點.

（此時，班級氣氛非常活躍，也許是體會到了數學學習的成功的喜悅）

追問5：剛才大家找到了多種方法，那么，它們的共同之處是什么？

全班學生：都需要過GC有一個平面與AB1M相交，運用線面平行的性質定理，從線面平行得到線線平行.

追問6：線面平行除了可以運用性質定理得到線線平行外，還可以得到面面平行，如何在此題中運用呢？

（學生陷入了沉思，偶爾會有人用手來回比畫）

學生10：作BB1的中點O，連接OM，OG，易得CO∥面AB1M，CG∥面AB1M，CG∩CO=C，則面OCG∥面A1BM. 由面面平行的性質定理可知OG∥AB1，O為中點，G亦為中點.

追問7：通過我們的努力，我們不僅理解了錯誤的原因，還奇跡般地得到了多種解法，在剛才的過程中，你有哪些收獲？

（學生相互交流討論，教師補充，對這個題目的方法進行總結和反思）

在上述教學過程中，針對學生的錯誤，教師設置了五個層次的追問：第一層次（追問1）可以讓學生深刻理解自己的解法為什么錯；第二層次（追問2、3）為學生解決此題提供了一個思路，并有效地鞏固了線面平行的性質定理；第三層次（追問4）讓學生從多個角度去運用線面平行的性質定理，在理解線面平行的性質定理的關鍵之處的同時，也激活了學生的思維；第四層次（追問5、6）可以讓學生認識到線線、線面、面面三種平行之間的聯系；第五層次（追問7）是一個總結提升的過程.

通過教師的問題，讓學生沿著問題逐步思考，找到錯誤的原因，再一步步尋求解決問題的辦法. 在尋找錯誤原因的過程中，教師沒有直接告訴學生哪里錯了，而是巧妙地設計問題，讓學生自己去發現錯誤緣由. 找到錯因后，不急于告訴學生該題的解法，而是通過追問，讓學生在教師的引導下，尋求解決問題的方法. 教師的追問不僅開闊了學生的視野，探究了該題的多種解法，更重要的是在師生共同探究該題的過程中，拓展了學生的思維，調動了學生學習的積極性和思考的主動性，凸顯了學生的主體性地位.數學課堂也由此變得更加精彩！

如果說教學是一門藝術，那么教師和學生都是藝術家，課堂則是藝術家們共同為藝術而不斷追求的圣地. 只要我們教師擁有一顆善于發現的眼睛，就能在課堂收獲意想不到的驚喜. 面對學生的錯誤，我們不妨把它當作教學的原材料，以此為突破口，進行有效追問. 只要我們善于抓住教學契機，課堂將真正成為我們藝術創作的天堂！