體驗：讓學生真正理解數學知識

傅佳俊

[摘 要]體驗學習，是指學生參與特定的數學活動，經歷數學知識形成和應用的過程，積累個人的經驗，從而獲取知識和應用知識解決問題的學習方式。恰當、適機地運用體驗學習，能幫助師生突破教學重、難點，讓學生真正理解所學的數學知識。

[關鍵詞]體驗 ?算理 ?建模 ?錯誤

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2016）01-013

“紙上得來終覺淺，絕知此事要躬行。”從這句話中我們不難明白，要想認識事物的本質，往往需要自己親身去嘗試，才能真正感悟其中內隱的道理。在追尋“讓學生真正理解知識”的數學課堂目標下，體驗無疑是一種有效的學習途徑，既能突破教學的重、難點，又能讓課堂教學呈現別樣的精彩。

一、體驗，讓概念更清晰

概念既是數學知識的基礎，又是構成數學教材的基本元素，還是數學思想與方法的載體。因此，正確理解數學概念是學生掌握數學基礎知識的前提。但許多數學概念具有抽象性，有些時候教師花了大力氣講解，可學生還是似懂非懂，不能真正理解所學概念。由此，使學生對數學概念有清晰的認識，是我們必須首先要解決的問題。

案例：教學“毫米、分米的認識”

1.利用實物，感知毫米

師：看來，同學們對毫米已經有點了解了。下面，請你從老師為同學們準備的信封（內有電話卡、1分硬幣、1元硬幣等物）中找出1毫米的物品。

生：電話卡、1分硬幣是1毫米。

師：電話卡的哪里是1毫米？1分硬幣的哪里是1毫米？請用手指出來。

……

2.借助實物，體驗毫米

師：校信通卡人人都有，這個卡的厚度剛好是1毫米。讓我們借助這個卡，再來感受一下這個神奇的1毫米。請大家像老師這樣用大拇指和食指夾住卡片，然后輕輕地抽出卡片，現在兩個手指間的空隙就是——（生：1毫米）保持這個動作，手指不能抖動哦，同桌互相看一看，好嗎？保持了這么長的時間，你手指間的空隙還是1毫米嗎？把你的卡插回去，有沒有覺得太寬或太緊？

師：請你閉上眼睛，想一想1毫米到底有多長。（生閉眼想）現在睜開眼睛，老師相信大家已經把它深深地記在心里了。1毫米這么小，你會用嗎？

……

通過教學，使學生了解和記住毫米這個數學名詞不難，但1毫米到底有多長？如何幫助學生構建1毫米的概念？上述教學中，教師為幫助學生建立起1毫米的直觀印象，設計了看卡片、看硬幣、夾卡片、記厚度等體驗活動，引導學生借助自己的動手操作來幫助記憶，使學生對1毫米留下了深刻的印記。這樣的深度體驗，既揭示了概念的內涵，又使學生把握了概念的外延，為學生今后用毫米解決問題打下了扎實的基礎。

二、體驗，讓算理更明白

計算教學一直被認為是一塊“難啃的骨頭”，教師教得累，學生學得苦，但教師累過了，學生苦過了，遺憾的是學生還是不懂，尤其對算理一知半解。怎么辦？下面的教學預設，也許能給大家有益的啟示。

案例：教學“有余數的除法”

為順利突破教學難點——余數要比除數小，教師預設了以下兩種策略，意在借體驗破難點。

策略1：在學生用小棒擺獨立正方形的操作中，特別是不能擺一個獨立的正方形時，課件交替出示兩種圖示法，這樣可以使學生明確當小棒數小于4根時不能擺一個獨立的正方形，從而有助于學生對“余數比除數小”這一教學難點的理解。然后將兩張圖片組合在一起（見圖1），先數一數多出來幾根小棒，再擺一擺，發(fā)現不能擺成一個正方形。

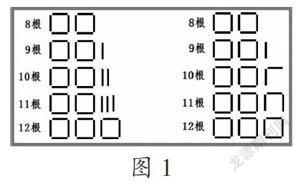
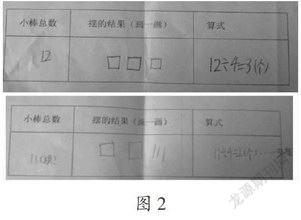
策略2：給每個小組都準備10～12根不同數量的小棒，請學生用手中的小棒擺出獨立的正方形，并把擺的結果以及所列算式寫在記錄單（見圖2）上。這樣，學生不僅有充裕的時間去拼擺，而且能對自己的成果進行檢查和修改。

上述教學，教師根據知識的系統(tǒng)性以及二年級學生的思維特點，設計了有效的操作體驗活動，既深化了學生對余數意義的直觀理解，又順理成章地驗證了“余數是否小于除數”這一結論的普遍性。學生在操作體驗中發(fā)現問題，然后通過教師的正確引導，充分感受到在平均分時會有剩余的情況出現。這樣教學，使學生更好地理解了余數和有余數的除法的含義。上好一節(jié)數學課，關鍵是讓學生真正地參與進來，充分調動學生的各種感官，引導他們自主發(fā)現新知，使學生在學習過程中感受到“數學源于生活，用于生活”。

三、體驗，讓建模更輕松

《數學課程標準》明確指出：“讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程，進而使學生獲得對數學理解的同時，在思維能力、情感態(tài)度與價值觀等多方面得到進步和發(fā)展。”因此，教師在數學教學中既要重視學生學習的結果，又要關注學生自主建立數學模型的過程，讓學生在進行探究性學習過程中，科學、合理、有效地建立數學模型。

案例：教學“植樹問題”

（學生前期自主探究、交流“在20米和30米的路上，每隔5米種一棵樹”的情況，師形成以下板書）

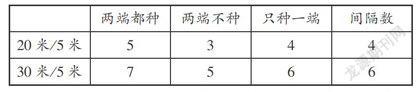
師：假如一條路有100米，在它的一邊每隔5米種一棵樹，要種幾棵？用自己喜歡的方式，求出要種幾棵樹，可以只算一種情況，也可以算出三種情況。（學生開始操作體驗，有畫圖的、計算的、找規(guī)律的）

師（問畫圖的學生）：你畫了幾棵樹？數一數，間隔數都是20嗎？

師：計算的同學的答案是怎樣的？你們的間隔數是怎么來的？

師：假如一條路有200米，在它的一邊每隔2米種一棵樹，要種幾棵？ （生答略）

師：通過這幾種情況的解答，發(fā)現畫圖很麻煩時，要求出棵數的關鍵是什么？（生答略）

師：在一條長10000米的路的一邊種樹，如果知道了間隔數，你能求出種樹的棵數嗎？假如不知道每隔幾米，只說有500個間隔或2000個間隔，你怎么辦？

師：如果現在有N個間隔，種樹的棵數怎么求？

[師結合學生交流，隨機形成如下板書（接上表）]

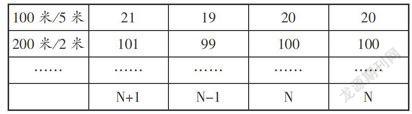
師：觀察表格，橫著看，你有什么發(fā)現？（使學生明確：“兩端都種”比間隔數多1，“兩端不種”比間隔數少1，“只種一端”與間隔數一樣）豎著看，你又有什么發(fā)現？（所有的“兩端都種”，都是+1;所有的“兩端不種”，都是-1;所有的“只種一端”，都相等）

……

數學規(guī)律的得出、數量關系的總結，只有通過一定量的體驗，學生才有可能理解。上述教學中，教師先讓學生找尋在20米和30米路上植樹的棵數，這兩個問題相對簡單，學生通過畫圖能準確、快速地找出三種不同情況的答案。然后教師又設計了在100米的路上植樹的問題，顯然這個長度通過畫圖解決已經有一定麻煩了，但學生還是畫出來了。接著，200米和1000米路長的出現，促使學生不得不去思考解決問題的新方法，提煉出蘊含其中的規(guī)律。最后，根據“N個間隔”來決定三種情況的植樹數量，使學生輕松建模并解決問題。在畫圖解決和畫圖不能解決的認知沖突產生時，教師及時引導學生思考：“畫圖太麻煩了，怎么辦？”同時，教師又通過橫著看和豎著看這兩個經典提問，引領學生及時地從畫圖數數轉向尋找數量關系，體會到解答“植樹問題”的關鍵所在。在這個學習過程中，學生的思維逐漸從具體走向一般，從形象思維向抽象邏輯思維過渡。這樣教學，使學生不再死記硬背某些規(guī)律和數量關系，而是真正理解了所學的數學知識。

四、體驗，讓錯誤更珍貴

在課程改革理念指引下，數學課堂上生成的錯誤作為一種資源正被大家逐漸重視，但教師在應對過程中還存在不予采用、用之不妥、刻意回避等問題，反映出教師對錯誤資源的應用意識和應對能力有待提升。因此，教師要相信學生的自我糾錯能力，并在教學過程中運用合適的應對策略，引導學生主動發(fā)現、改正錯誤，為學生提供辨別、分析、判斷、推理的機會，讓學生經歷由錯誤到正確的體驗過程。

案例：教學“分數的初步認識”

教學“把一個月餅平均分成兩份，每份是1 / 2”后，教師設計了“動作操作，比較感悟”的教學環(huán)節(jié)：讓學生在長方形、正方形、三角形等不同形狀的紙片中，選擇一張自己喜歡的紙片折出1 / 2并涂色表示。學生匯報結束后，正當教師要提問時，一個男生舉起了手。

師：為什么？

生1：這個長方形沒有平均分，因為兩部分圖形對折后沒有重合。

師（對創(chuàng)作這幅作品的學生）：你覺得自己的作品有沒有平均分？

生2：不知道怎么說，我想應該是平均分的。

師：其他同學知道嗎？你們有辦法證明嗎？

生3：這個很簡單呀！我們只要沿著折痕把這個長方形剪開，得到的兩個三角形就可以重合在一起了。

師：不錯的辦法！我們來試一試。

師（在學生完成操作后）：現在還有同學有疑問嗎？

……

平均分是分數產生的前提，沒有平均分就沒有分數，所以真正理解平均分是本課教學的重點。上述教學中，生1的質疑完全出乎教師的意料，這是一個偏離預設的即興生成，教師的應對之法值得圈點，既珍視生成的資源，尊重學生的質疑，又調整了預設的教學流程，并在學生自主學習過程中增加了動手試一試的實踐環(huán)節(jié)。通過體驗，學生的思維激活了，疑問消除了，認知深刻了。所以，課堂教學中，教師需要把握生成資源，重構學習主題，為學生提供展示思維、交流觀點的機會，最終達到“以學論教”的佳境。

蘇霍姆林斯基說過：“成功的體驗是一種巨大的情緒力量！”的確，成功的體驗能幫助師生突破教學重、難點，讓學生真正理解數學知識。

（責編 杜 華）