數學與專業課如何有機結合

范雪蓮

摘 ? ?要： 如今，在經濟危機這樣嚴峻的形勢下，各類學生的就業情況，屬職教類畢業生最好。其主要原因是，職教類學校重技能訓練，按照企業的要求，制訂教學計劃，開設課程，加強專業課的實際訓練，學生的技能水平大大提高，一畢業就能上崗操作，因而深受企業歡迎，在就業市場贏得了主動權。

關鍵詞： 職業高中 ? ?數學應用 ? ?電工專業

在職業高中開設課程，除了專業課以外，還要開設必要的文化課。如何安排好科目之間的關系，對于學生學習起到了至關重要的作用。下面針對專業特征談談數學在電工專業中的應用。

一、數學應用的廣泛性

數學的主要特征之一，就是應用的廣泛性。“廣泛”對現代數學來說就是人類活動，人類科學的幾乎所有的領域都要應用數學，與其他科學相比，這是十分獨特的。數學產生于人的實踐之中，即數學是在人的應用需要中發展起來的。萌芽時期的數學都具有直接的應用性，近代數學的大發展是由數學在科學技術中的應用開始的，應用促進了微積分學的產生（17世紀），此后分析數學、統計數學的發展都與應用有著直接的關系。隨著數學的發展，數學的應用能力不斷提高——不斷提供更有力的工具，因而可能在更廣泛的領域得到應用。

數學的應用為什么如此廣泛？那就是因為數學對于人的實踐和其他科學具有下述重要意義：數學為各領域的問題及其解決提供了科學的表述語言;為其他科學提供了一種抽象思維的模式，即充分發揮人的主觀能動性和創造性思維能力，解決各種現實問題的途徑;為解決各領域的問題提供計算方法。

二、職業高中數學教學的現狀

職高學生從小學到現在長時間的數學學習過程中，普遍存在概念不清、推理不嚴謹等問題，沒有合理的知識結構，故而對數學產生厭惡和排斥情緒。同時學生學習目標不夠明確，任務觀點，未能切實感受到數學在他們專業上的用途，以至于不思上進，甚至于以破壞課堂紀律來反抗，作業不認真，抄襲應付，學生學得很無奈。對于數學老師而言，也是竭盡了全力，疲于奔命，可是卻收效甚微，徒勞無功。久而久之，形成惡性循環，導致教學失敗。

如何改變現狀呢？著眼于數學和電工專業的結合，使學生切實感受數學的重要性，能夠重視數學，提起對數學的學習興趣。

三、如何將數學應用到專業課中

不同專業課教學所用到的數學基礎知識是不同的。為提高課堂教學效率，必須將數學課程與專業課程資源有效整合。具體做法是：鉆研教材，尋找關聯知識;總結、提煉出兩個學科教學中相通的數學思想方法;創設問題情境，復習舊知、聯系新知，區分數學知識在電工專業中具體應用的不同點;由專業課需求確定數學教學的重、難點。

1.應用數學的函數圖像

函數可以通過坐標系轉化成圖形，從而直觀地研究。數和形是數學的兩大根基，以前毫不相干，正是坐標系的出現，把作為“數”的函數轉化為作為“形”的圖像，從此數學發展得更蓬勃。把函數解析式表示成圖像，我們能從中獲取很多信息。直接地說，能從函數圖像上看出函數的變化趨勢，形象化對解題起到非常重要的作用。

例如，可以用圖像表示電壓與電流的關系。如圖，以電壓為橫坐標，電流為縱坐標，可畫出U-I關系曲線，稱為電阻元件的伏安特性曲線，如圖（1）所示。當電阻元件伏安特性曲線是直線時，稱為線性電阻。即此電阻元件的電阻值R可以認為是不變的常數，直線斜率的倒數表示改電阻元件的電阻值。如果不是直線，則成為非線性電阻。利用圖像，就可很直觀地看出電阻是否是線性電阻。

再如，交流電中，最基本的就是正弦交流電，表征正弦交流電的物理量均可利用圖像。正弦交流電的電動勢的解析式為e=Esin（ωt+φ），利用正弦型曲線來表示，橫坐標表示時間t或角度ωt，縱坐標表示隨時間變化的電動勢的瞬時值，在波形上可以反映出最大值、初相和周期等。

圖（2）（a） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?圖（2）（b）

圖（2）（c） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖（2）（d）

如圖（2）（a）正弦曲線的初相為零，圖（b）的初相在0～π之間，圖（c）的初相在-π～0之間，圖（d）的初相為±π。在分析初相時，如果借助了正弦曲線，就可很形象地看出，如果初相是正值，曲線的起點就在坐標原點的左邊;如果初相是負值，則起點在原點的右邊。為了比較幾個正弦量的相位關系，也可以把它們的曲線畫在同一坐標系內。但由于它們的單位不同，故縱坐標上電壓、電流可分別按照不同比例表示。三相對稱電動勢的表示上，正弦曲線的優勢更能夠體現出來。若以第一相電動勢的初相角為0°，則第二相為-120°，第三相為120°，那么各相電動勢的瞬時值表達式則為

e=Esinωt，e=Esin（ωt-120°），e=Esin（ωt+120°）。

如圖（3），從圖像上很容易看出，三相對稱電動勢在任一瞬間的代數和為零。

圖（3）

從一系列實例上也可看出，數學的圖像對于電工中某些物理量的表示起到了極其重要的作用，能加深學生的理解，也能簡化某些概念的表述。

2.應用數學的空間想象力

培養空間想象力是數學教學的主要任務之一。在《電工基礎》這本教材上，對于電磁感應這個章節的內容，就需要應用數學中的空間想象能力。在用右手定則判斷感應電流方向及用左手定則判斷感應電動勢的時候，就要利用空間想象力，圖上只能畫出二維的圖形，對于三維圖形，如果沒有扎實的數學功底，是很難辦到的。

3.應用數學的邏輯思維能力

邏輯學是研究思維形及思維規律的科學，思維的形式包括概念、判斷和推理之間的結構和聯系。概念是思維的基本單位，通過概念決定事物是否具有某種屬性就是判斷，由判斷推出另一個判斷的思維形式就是推理。用數學的方法研究推理就是數學邏輯。在中學數學教學中，也有很多相關邏輯的內容。在學習邏輯內容時，前提是要熟悉邏輯連接詞。在數字電路中，同樣也有邏輯電路。下面談談這些簡易邏輯代數在電工中的應用。

（1）非

數學中對于非得表述：對于每一個命題，都有一個與它意義相反的命題，這個命題就是原來命題的否定，其真值表見圖（4）a。電路中的非門電路，是指輸出信號與輸入信號存在著“反相”關系，即輸入信號為低電平時，輸出信號為高電平;而輸入信號為高電平時，輸出信號為低電平。非門只有一個輸入端和輸出端。比如輸入為1，則輸出為非1，即0;反之，輸入為0，則輸出為非0，即1。非門的真值表見圖（4）b。

圖（4）（a） ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖（4）（b）

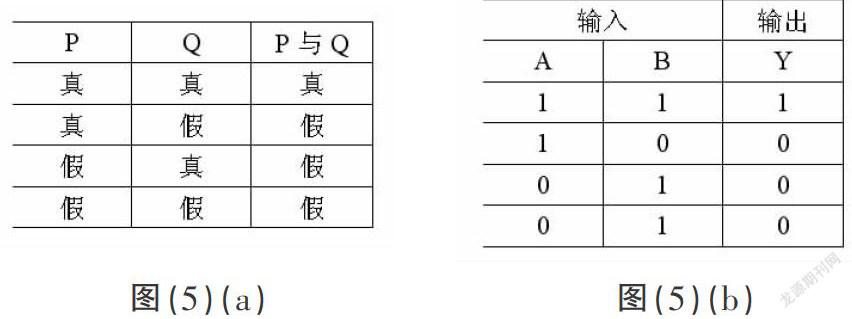
（2）與

設P和Q是兩個命題，“P與Q“真值表見圖（5）a。電路中的與門電路假如有兩個輸入端A和B，一個輸出端Y，Y=AB其真值表見圖（5）b。與門電路的輸入端可以個有多個，只有當輸入端全為1時，輸出才為1，其余都是0.

圖（5）（a） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖（5）（b）

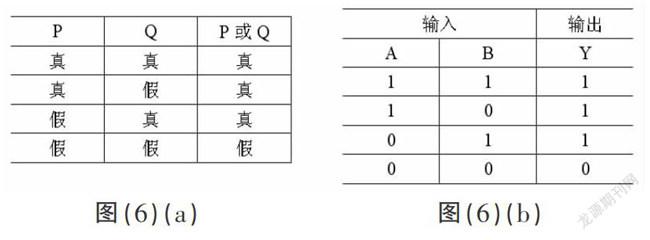
（3）或

設P和Q是兩個命題，“P或Q”真值表見圖（6）a。電路中的或門電路，假如有兩個輸入端A、B，有一個輸出端Y=A+B，其真值表見圖（6）b。同樣，或門電路也可以由多個輸入端，只有當輸入端全為0時，輸出端才為0，i其余都是1.

圖（6）（a） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 圖（6）（b）

光從概念看，數學和電工是統一的。那么怎么體現出數學邏輯的優越性呢？各個邏輯組合起來有規定的運算法則。例如：=P，=∨，=∧，將這一系列運算法則運用到組合邏輯門電路中，它的優勢能得以體現了。常見的簡單組合門有：與非門Y=;或非門y=;與或非門y=等。在這些組合門中，利用邏輯代數運算法則，得其真值表，能夠簡便而正確地得知輸出端的情況。邏輯代數是研究邏輯電路的數學工具，利用邏輯代數可以判定一個已知邏輯電路的功能或根據需要的邏輯功能研究和簡化一個相應的邏輯電路。任何組合邏輯電路其輸入和輸出狀態的邏輯關系可用邏輯函數式表示，反之，任何一個邏輯函數式，總可以用組合邏輯電路與之對應。由于邏輯代數有一些基本的運算定律，應用這些定律可以把一個復雜的邏輯函數式恒等化簡。由于每一個邏輯函數式都體現著一個電路，因此邏輯函數式的化簡就意味著電路的化簡。可見邏輯代數的作用，就在于把邏輯電路的簡化問題變成相應的邏輯函數式的簡化問題，為設計和認識邏輯電路帶來方便。

例如：設計一個體現Y=AB+AC函數式的邏輯電路。

解：根據題意，可畫出圖（7）（a）的電路，但函數式化簡后得

Y=AB+AC=A（B+C），可化簡成圖（7）（b）的電路。

圖（7）（a） ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?圖（7）（b）

4.應用數學的運算公式

數學的公式眾多，是一切運算的基本工具。在電工專業中更應該靈活運用數學公式。比如，可以用復數表示正弦交流電，具體方法如下：用復數的模表示正弦電壓或電流的有效值，用輻角表示正弦電壓或電流的初相角。

例如：已知兩個正弦交流電流為

i=6sin（ωt+120°）A，i=8sin（ωt+30°）A，求它們的和。

解：i和i分別用復數表示為=6（cos120°+jsin120°）≈（-3+j5.2）A

=8（cos30°+jsin30°）≈（6.9+j4）A

所以，I=+=（-3+j5.2+6.9+j4）A=（3.9+j9.2）A

=10（cos67°+jsin67°）A

最后將電流寫成對應的解析式i=10sin（ωt+67°）A.

從例題中可以看出，用復數表示正弦型交流電可以簡化解題過程。數學公式在電工中的應用數不勝數，這里就不一一列舉了。

總之，數學在電工專業中的應用非常廣泛，不管是在什么內容中，時時刻刻都有數學的影子。出于傳統教學模式的弊端，如何發揮數學在電工專業中的應用，是當今職教類學校電工專業中數學教學的首要任務。一是可以提高學生對數學的學習興趣，二是可以提高數學課堂教學效率，三是可以與專業課相輔相成，互相促進。數學任課老師可以根據教學需要適當地安排教材內容，按尺度適當刪選、補充，以與專業課相結合為基礎，廣納教材，精選精華，在數學應用方面下工夫，甚至于編寫分別適合各個專業的校本教材。

參考文獻：

[1]周紹敏.電工基礎.

[2]陳其純.電子線路.