試探整體把握教材的教學策略

洪亮

根據新課標總體目標安排，教材將數學知識分成“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”四個領域。然后根據學段目標和學生的年齡特點、認知水平，教材又將選定的內容切分成若干個單元，分散到不同學段、不同年級、不同學期。因此，我們在教學中就必須關注學生不同階段的需求。采用循序漸進、螺旋上升的策略。逐步達標。同時，我們也要關注教材編排的整體特點，幫助學生理解知識之間的實質性聯系，展示知識的整體性和數學方法的一般性，從發生、發展到深化、運用和拓展，打通不同階段的顯性知識及其蘊含的數學思想方法上的聯系，使它們形成一個完整的整體，形成良好的認知結構。具體在實踐中，我們應緊扣知識的數學本質，找準知識的生長點、衍生點，選擇、重組或創編教學內容，讓知識有邏輯地生長，多方向連接。并借助生長慣性擴展知識的廣度，增加知識的深度。

一、整體把握教材，使基礎知識和基本技能的教學呈現出一條動態發展的主脈絡

教材內容的安排，常常是符合知識發生、發展的線索，能尊重學生認知發展的特點，體現了教學內容設計的層次結構。我們在教學中必須研讀教材。深入理解教學內容的前后聯系。把握住教學動態發展的主脈絡。

1 聯結：貫通前后，整體建構

如“連除問題”的教學，我從連乘入手。采用倒推的策略，幫助學生理解數量關系，這樣就從整體上建構了連除與連乘問題的實質關聯。

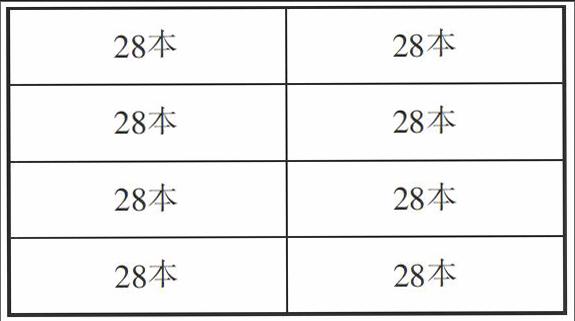
出示復習題：學校圖書室有兩個書架，每個書架都有四層，每層可以放28本書，這兩個書架一共可以放多少本書？

學生列式解答：2×4=8（層），8×28=224（本）；或者28×4=112（本），112×2=224（本）。也有學生借助假設思路這樣列式：把兩個書架并排放。先算一大層有2×28=56（本），再算四大層有56×4=224（本）。

教師將學生的三種思路畫成一張圖（如下），指出：求一共有多少本書，其實就是求一共有多少個28本書。

接著教師將表格中的28本這個信息隱去，添上兩個書架一共224本這個信息。問：這道題是什么意思？你能計算出每個書架每層有多少本書嗎？

學生對照表格，自然而然地聯想到采用“倒推”的策略進行“平均分”。

解法1：224÷2=112（本），112÷4=28（本）；

解法2：224÷4=56（本），56÷2=28（本）；

解法3：2×4=8（層），224÷8=28（本）。

這里的三種解法對應原來連乘問題的三種解法，學生很自然地聯想到倒推的思路，一下子把握住了連除問題的數量關系的本質核心，也就把連除問題、連乘問題結為一個穩固的結構整體，學習自然輕松高效。

2 穿插：相互支持，交叉應用

教材為了讓各領域內容相互支持，各種思想方法交叉應用，常常在單元內容的安排中適時出現一些其他領域的學習內容，使教學做到新中帶舊。新舊交融。如教學“面積單位”時，呈現一些軸對稱圖形，讓學生數數含有多少個面積單位。

比如，教學“年、月、日”單元時，安排一次綜合實踐活動。教材要求學生應用統計的方式，了解和呈現班級里學生的生日情況（如下圖），教學時可組織學生先在小組內統計，再交流匯總，得到全班的統計數據。然后讓學生制作條形統計圖，并要求學生能看著統計圖，回答圖中的兩個問題。這一過程既能鞏固年、月、日的基本知識。又圍繞生日綜合地運用了年、月、日的知識和統計的方法。

這種交叉運用，還體現在對教材的準確把握和創新設計上。比如“平均數”的教學，我特意指導學生畫長方形來移多補少，借助數形結合，從數學本質上認識和把握教材的要旨，取得了較好的效果。

3 孕伏：著眼未來，水到渠成

教學就如同培育學生一顆自由生長的種子，生命的培育不是一蹴而就的，它是一個漫長的歷史發展過程。學生對數學知識的理解和掌握，需要我們精心培育，逐步滲透，有些知識需要提前孕伏，使學生達到自然的水到渠成。如教學“兩位數乘兩位數”時，教材出示題組練習（如下）：（1）25×16 （2）34×21 （3）13×29 25×4×4 34×20+34 13×30-13

意在通過練習對比，使學生發現每組算式雖然形式不同，但結果相等，為后面學習乘法的運算律作孕伏。這種滲透教學，我們應把握好教學的度，做到到位而不越位。我是這樣做的：先讓學生獨立解答。然后組織討論：為什么每一組的得數都一樣呢？這里面有什么奧秘呢？對第一題。學生基本上能看得懂（只要能說出4×4=16即可）：對第二題也能理解，借助豎式可以清楚地看出34×21，就是先算34×1，再算34×20，最后再相加；而對于第三題。不少學生迷糊了。我則依然借助豎式，讓學生說一說豎式計算過程：先算13×9。再算13×20。最后把兩次相乘的積相加。在此基礎上。我引導學生：豎式的計算過程。其實就是先算9個13，再算20個13，這樣合起來正好是29個13，對照這樣的思路。想一想13×30-13是什么意思？學生受此啟發。恍然大悟：先算30個13。再去掉一個13，也是29個13。上面的教學過程，緊緊抓住豎式計算過程來分析展開，學生易于理解和接受，為以后進一步學習乘法分配律作了很好的孕伏。

二、整體重建教材，使數學活動經驗和數學思想成為主導學生發展的核心動力

教材的編寫有一個重要原則，就是要呈現不同數學知識之間的聯系。這給我們的教學以啟迪：我們在分析教材、處理教材的時候，要關注數學知識之間存在的實質性聯系。這種聯系，不僅僅體現在相同的內容領域，也體現在不同的內容領域。幫助學生理解類似的實質性聯系，是數學教學的重要任務。

1 貫穿：把握階段，關注發展

數學中有一些重要內容、方法、思想是需要學生經歷較長的認識過程，逐步理解和掌握的。因此。教材在呈現相應的數學內容與思想方法時，總是采用逐級遞進、螺旋上升的原則，既體現出一定的教學階段性，又要把握住教學的發展性。比如，教學“三位數除以一位數（筆算）”時，我們應始終做到筆算前“估計-感受”、筆算時“思考-體會”、筆算后“比較-綜合”。這是思維方法上的一種貫穿。

“估計-感受”：筆算前，在具體情境里估計得數，感受應該先把被除數的哪一部分除以除數，“思考-體會”：引導學生進行比較理性的思考、感悟，體會商的最高位的規律。“比較-綜合”：即通過比較與研究。得出三位數除以一位數的計算法則。這種思考方法，應該作為一種基本的教學策略，貫穿于筆算教學的始終，不僅是現在的三位數除以一位數，后面學習兩位數的乘法時也是如此。

2 整合：主題設計，深度梳理

如筆者發現“正方形”是本冊教材的一個重要焦點，積聚了本學期很多重要內容和知識點。分數、小數教學中的正方形，到面積單位中的正方形，到乘法計算中的正方形，再到最后的平方數，集中體現了數形結合思想，因此我設計了說說“正方形”的主題課，讓學生享受一次數學結合思想生長的美妙“旅途”。學生從對正方形圖形的聯想到正方形可以表示面積單位，可以表示小數的計數單位，可以表示電影院座位的個數。再到如何計算邊長為10的正方形所含小方塊的個數的巧妙方法。如有的學生說：1+3+5+7+9+11+13+15+17+19=100，還有的學生想到從西南到東北的對角線來計算方塊：1+2+3+4+…+10+9+8+…+3+2+1=100。真是太奇妙了！

上面的教學，從正方形這個圖，變成各種各樣的數，學生深切感受到數形結合所帶來的數學力量是如此偉大，又是如此美麗。

由此筆者以為，我們在教學中應在充分理解教材編寫意圖的基礎上，結合學生的認知特點，有目的、有意圖地取舍、剪接、組合、加工，讓教材所蘊含的數學思想、數學文化得到淋漓盡致的展示。我們只有站在教材的角度，認清知識本源的深度，同時藝術化地加工教材，才能讓教師的教成為學生發展的“助推器”。

3 營造：長遠規劃，潛移默化

數學教學是一個不斷延續的成長過程。很多老師往往忽視開學第一課的設計，常常安排復習上一冊的教學內容，或者復習與第一單元相關的內容，為新課學習作好鋪墊。而我一般會用第一課組織學生讀一讀、說一說對一本書的總體感受。

首先，我會讓學生打開課本，讀一讀目錄，看看這學期我們要學習哪些內容，說一說這些內容中哪些是我們以前曾經學過的類似知識，哪些是我們沒有遇到過的新內容，哪些內容學生最感興趣。在說一說時。我會給學生一些問題：如認識分數和認識小數往往有著密切聯系。從本質上講，它們說的是一回事，讓學生產生一個個奇怪的問號……

接著，我會讓學生對這些內容進行分類：有意識地指導學生將全書內容分為數與量、圖形、統計、綜合實踐等。在此基礎上，我提出：你們覺得怎樣能學好這些內容呢？有的學生說……

最后，我再和全體學生共同討論定出一份學習計劃與進度安排，并貼在墻上。

這樣從開學第一天就把學生的數學學習領到一個高地進行展望，我發現這一小小的改動，對學生一學期的學習都具有重要意義，尤其是到了期末，學生對整冊書的知識點會有一種自然而然的提升。